郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

35th Conference on Neural Information Processing Systems (NeurIPS 2021) 

Abstract

　　最近的研究表明，深度强化学习智能体很容易受到智能体输入上的小对抗性扰动的影响，这引发了人们对在现实世界中部署此类智能体的担忧。为了解决这个问题，我们提出了RADIAL-RL，这是一个原则性框架，用于训练强化学习智能体，提高其对l_p-范数有界对抗性攻击的鲁棒性。我们的框架与流行的深度强化学习算法兼容，并通过深度Q学习、A3C和PPO展示了其性能。我们在三个深度RL基准（Atari、MuJoCo和ProcGen）上进行了实验，以展示我们的鲁棒训练算法的有效性。当针对不同强度的攻击进行测试时，我们的RADIAL-RL智能体始终优于先前的方法，并且在训练时计算效率更高。此外，我们提出了一种新的评估方法，称为贪婪最坏情况奖励（GWC），以衡量深度RL智能体的攻击不可知鲁棒性。我们表明，GWC可以被有效地评估，并且是对在最坏对抗性攻击序列下奖励的良好估计。用于我们实验的所有代码都可以在https://github.com/tuomaso/radial_rl_v2中获取。

1 Introduction

　　深度学习在各种具有挑战性的领域取得了巨大成功，从计算机视觉[1]、自然语言处理[2]到强化学习(RL)[3, 4]。然而，对抗性样本[5]的存在表明，深度神经网络(DNN)并不像我们预期的那样鲁棒和可信，因为微小且往往难以察觉的扰动可能导致对最先进的DNN的错误分类。不幸的是，对抗性攻击在深度强化学习中也被证明是可能的，其中观察空间和/或动作空间中的对抗性扰动可能导致深度RL智能体的任意糟糕性能[6, 7, 8]。由于深度RL智能体被部署在许多安全关键应用中，如自动驾驶汽车和机器人，因此开发鲁棒训练算法（也称为防御算法）至关重要，以使最终训练的智能体对对抗性（和非对抗性）扰动具有鲁棒性。

　　已经提出了许多启发式防御来提高DNN对图像分类任务的对抗性攻击的鲁棒性，但它们在对抗更强的对抗性进攻算法时往往失败。例如，[9]表明，13种这样的防御方法（最近在著名会议上发表）都可以被更先进的攻击打破。启发式防御的一个新兴替代方案是基于鲁棒性验证或认证边界的防御算法²[10, 11, 12, 13]。这些算法产生鲁棒性证书，使得对于指定的l_p范数距离内的任何扰动，训好的DNN将在给定的数据点上产生一致的分类结果。沿着这条线的代表性工作包括[11]和[14]，其中，通过在具有适当训练计划的损失函数中包括鲁棒性验证边界，学到的模型可以具有更高的认证精度，即使验证器为没有鲁棒训练的模型（也称为标准模型）生成松散的鲁棒性证书[14]。在这里，认证的精度被计算为在给定扰动幅度下保证被正确分类的测试图像的百分比。

　　然而，大多数防御算法都是为分类任务开发的。很少有防御算法被设计用于深度RL智能体，这可能是因为RL中存在分类任务中不存在的额外挑战，包括信度分配和缺乏固定训练集。为了弥补这一差距，在本文中，我们提出了RADIAL(Robust ADversarIAl Loss)-RL框架来训练鲁棒的深度RL智能体。我们表明，RADIAL可以通过使用精心设计的基于鲁棒性验证边界的对抗性损失函数来提高深度RL智能体的鲁棒性。我们的贡献如下：

• 我们提出了一种新的鲁棒深度RL框架RADIAL-RL，它可以应用于不同类型的深度RL算法。我们在三种流行的RL算法DQN[3]、A3C[15]和PPO[16]上演示了RADIAL。
• 我们展示了RADIAL智能体在Atari游戏和MuJoCo中的连续控制任务中的卓越性能：我们的智能体与[17]相比，训练的计算效率高出2-10倍，并且可以比现有工作[18, 17]更好地抵抗多达5倍强的对抗性扰动。
• 我们还使用ProcGen基准评估了鲁棒训练对智能体泛化到新水平的能力的影响，并表明我们的训练还提高了对看不见的水平的鲁棒性，即使面对ε=5/255的PGD攻击也能获得高奖励。
• 我们提出了一种新的评估方法，贪婪最坏情况奖励（GWC），用于有效地（在线性时间内）评估RL智能体在最强对手（即最坏情况下的扰动）。

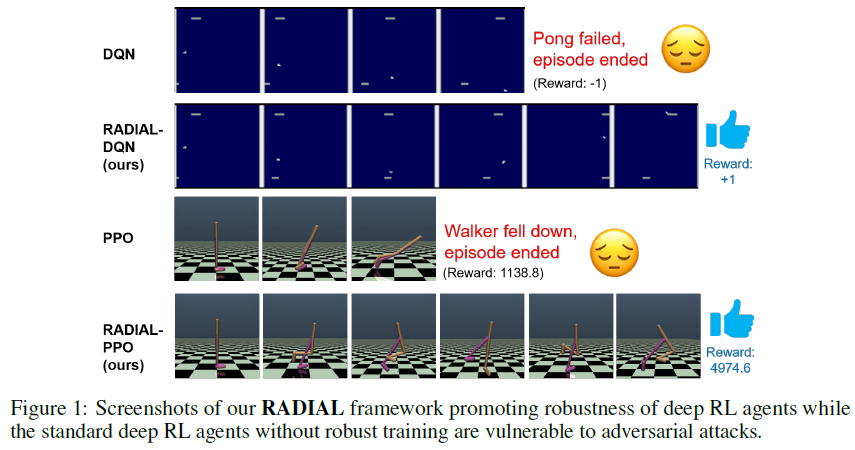
2 Related work and background

2.1 Adversarial attacks in Deep RL

2.2 Formal verification and robust training for Deep RL

2.3 Basics of Deep Reinforcement Learning

3 A Robust Deep RL framework with adversarial loss

　　在本节中，我们提出了RADIAL-RL，这是一个用于训练对抗性攻击的深度RL智能体的原则性框架。RADIAL通过利用现有的神经网络鲁棒性形式验证边界来设计对抗性损失函数。我们首先介绍了RADIAL的关键思想，然后在第3.1、3.2和3.3节中阐明了为三种经典的深度强化学习算法DQN、A3C和PPO制定对抗性损失的几种方法。在第3.4节中，我们提出了一种新的评估指标，贪婪最坏情况奖励（GWC），以有效评估智能体对输入扰动的鲁棒性。

Main idea. RADIAL框架的训练损失LRADIAL由两个项组成：

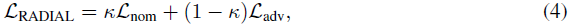
其中，L_nom表示标准损失函数，如公式(1)-(3)用于标准深度RL智能体，L_adv表示对抗性损失，我们将仔细设计该损失以考虑对抗性扰动。κ是一个超参数，用于控制标准性能和鲁棒性能之间的权衡，其值在0和1之间，并且注意，标准RL训练算法在整个训练过程中具有κ=1。在此，我们提出了两种原则性方法来构建L_adv，这两种方法都是通过神经网络鲁棒性证明边界[14, 12, 13, 11, 31, 32, 33, 34]：

　　#1. 构造扰动标准损失的严格上界（公式(9), (10), (7)）；

　　#2. 设计正则化子以最小化结果差异较大的动作的输出边界之间的重叠（公式(5), (6)）。

　　方法#1的动机很好，因为最小化扰动标准损失的严格上限通常也会降低真正的扰动标准损失，这表明策略在对抗性扰动下应该表现良好。或者，方法#2的动机是我们希望避免因为小的输入扰动而选择明显更糟糕的动作。

　　方法#1和#2的基础都在于鲁棒性形式验证工具，以导出输入扰动下神经网络的输出边界。具体而言，对于给定的神经网络，假设z_i(x)是具有输入x的神经网络的第 i 层的激活。鲁棒性验证算法的目标是计算神经网络的逐层下界和上界，表示为和，使得，对于具有||δ||_p ≤ ε的x上的任何加性输入扰动δ。我们将在Q网络（用于DQN）或策略网络（用于A3C和PPO）上应用鲁棒性验证算法，以获得Q和π的逐层输出边界。这些输出边界可用于计算方法#1在最坏情况的对抗性扰动L_adv下的原始损失函数的上界。类似地，如方法#2所提出的，逐层边界用于最小化输出间隔的重叠。为了提高训练效率，IBP[14]用于计算神经网络的逐层边界，但也可以直接应用其他可微认证方法[12, 13, 11, 31, 32, 33]（尽管可能会产生额外的计算成本）。我们的实验集中在p=∞上，以与基线进行比较，但该方法适用于一般p。

3.1 RADIAL-DQN

　　对于对偶DQN，优势函数A_Q用于决定采取哪种动作，而价值函数V_Q仅对训练很重要。因此，我们只需要使A_Q具有鲁棒性，并且Q函数的上下限为和，给予输入s界限为ε的扰动。在RADIAL中，我们提出了两种方法来导出对抗性损失L_adv；然而，由于空间限制，我们在正文中描述了具有更好经验性能的方法，而在附录中保留了另一种方法。

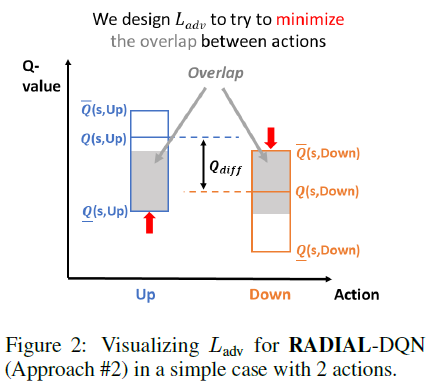
　　对于DQN，我们发现方法#2的性能更好。方法#2的目标是最小化不同动作的激活边界的加权重叠（图2）。其思想是只最小化鲁棒性能所必需的重叠。如果没有重叠，即使在扰动下，原始动作的Q值也保证高于其他动作，因此智能体不会在扰动下改变其行为。然而，并不是所有的重叠都同样重要。如果两个动作具有非常相似的Q值，重叠是可以接受的，因为在扰动下采取不同但同样好的动作不是问题。为了解决这个问题，我们添加了Q_diff加权，这有助于将与类似Q值的重叠乘以一个小数字，并将与不同Q值的重复乘以一个大数字。

　　最终损失函数如下：

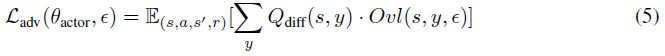
其中：

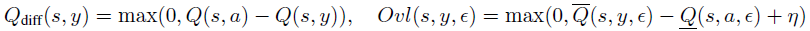
η = 0.5 · Q_diff(s, y)，a是所采取的动作。这里Ovl表示两个动作的边界之间的重叠（图2中的灰色区域）。为了提高额外的鲁棒性，激励网络具有裕度η（而不是简单地没有重叠）。我们设置η = 0.5 · Q_diff，使其为可达到的最大裕度的一半。请参阅附录F，了解有关此选项对裕度的重要性的实验和讨论。请注意，Q_diff被视为用于优化的常数（无梯度）。公式(5)在ε=0时减小到零。

3.2 RADIAL-A3C

3.3 RADIAL-PPO

3.4 New efficient evaluation metric: Greedy Worst-Case Reward

　　训练RL智能体对输入扰动具有鲁棒性的目标是确保智能体在任何（有界）对抗性扰动下仍能表现良好。这可以转化为最大化最坏情况奖励R_wc，这是在最坏对抗性攻击序列下的奖励。我们定义R_wc如下：，轨迹τ = (s₀, a₀, ... , s_T, a_T)，其中a_t, s_t, r_t分别从中抽取，并且R(τ) =。一种想法是评估每一个可能的轨迹τ，找出哪一个轨迹产生的奖励最小。然而，R_wc实际上是不可能评估的，因为对于每个状态s_t，找到一组可能动作a_t的最坏扰动δ_t是NP困难的，并且要评估的轨迹量相对于轨迹长度T呈指数增长，这很难计算。避免直接发现最坏情况扰动的一种可能方法是使用经验证的输出边界[12, 13, 11, 31, 32, 33]，这会在最坏情况下产生所有可能动作的超集，因此产生的总累积奖励是R_wc的下界。我们将此奖励命名为绝对最坏情况奖励（AWC）。注意，当策略和环境都是确定性的时，AWC是R_wc的下界。

　　然而，AWC仍然需要评估可能的动作序列的指数数量，这在计算上是昂贵的。为了克服这一限制，我们在算法1中提出了一种称为贪婪最坏情况奖励（GWC）的替代评估方法，该方法近似于期望的R_wc，并且可以以总时间步长T的线性复杂度有效地计算。GWC的想法是避免评估轨迹的指数数量，并使用简单的启发式方法来近似R_wc，方法是在每个状态下贪婪地选择Q值最低的动作（或A3C采取动作的概率）。我们在图4（附录E）中显示，GWC通常接近AWC，同时评估速度要快得多（总时间步长的线性复杂性）。关于基线工作[17, 18]中使用的度量的讨论以及AWC计算算法的完整描述见附录D。

4 Experimental results

4.1 Atari results

4.2 ProcGen Results

4.3 MuJoCo Results

4.4 Evaluating GWC

5 Conclusions and Future works

6 Limitations and Potential negative impact