学习笔记——博弈论
博弈论中玩家的选择均为对自己最有利の理论最优解.
文中提到的必胜状态和必败状态来自要求的游戏起始状态, 但不由其推得.
这句话可能有些抽象,我也不太会表达(重度社恐),所以举个例子:
\(nim\)游戏,3堆石子,分别为1,2,3.
最暴力的解法,我们枚举所有可能的状态,
然后把他们构成一个有向无环图——这也是博弈论中的一种最简单的思路
.在构图的过程中,针对这个{1,2,3}, 一定会有一种{1,2,2}.
但这个{1,2,2}是必胜还是必败与{1,2,3}无关.相反,{1,2,2}的状态可以决定 {1,2,3}的状态.
\(nim\)游戏
首先,有个很经典的问题——\(nim\)游戏:
有 \(n\)堆石子,两名玩家轮流选一堆取走若干个(不能不取).拿走最后一枚石子的玩家获胜,没有石子可取的玩家失败.
这个问题的求解方式很抽象:求所有石子的异或和.若为0,先手必败,否则先手必胜.
这是因为, 一个必败状态要么直接寄,要么只能转化成必胜状态.一个必胜状态一定能转化成必败状态.
由此可见,我们可以从状态的角度理解博弈论.我们可以把所有状态构成一个有向无环图.
每个状态要么先手必胜,要么先手必败.
如果一个状态只能转移到必胜,则其为必败;如果它能转移到必败,则其为必胜.
但如果不是有向无环图呢?状态转移中出现环怎么办?
可以利用递推,先推出尽可能多的状态.
如果一个已知的状态为必败,则所有指向它的状态均为必胜;
如果一个状态只指向已知的必胜,则其为必败.
直到不能推出更多状态为止.可以使用拓扑排序.
可以验证未被递推的状态即为平局.
一些例题
1.[ARC131C] Zero XOR
PS:下文中的\(S\)意义均相同,为剩余所有元素的异或和
首先强调两个有关异或的特殊性质,这是解这道题的关键:
首先我们可以大胆猜测一些易证明且关键结论,比如,在这道题里,n若为奇数,先手必胜。
很好证明:
首先我们知道,石子各不相同。再结合上面两个特殊性质,
我们易可得:整个游戏全程,只会有一种状态使得\(S\)为0.
而如果石子为奇数,两堆两堆的取,最后一定能得到只剩一堆的情况。
而当先手取完这一堆,\(S\)显然为0——所以中间不再存在其他能使\(S\)为0的状态。
那么解决了奇数,偶数就好解决多了。我们先去找找有没有一个\(w_i=S\)。
如果有,则先手必胜。
依然很好证明:
使用上面的特性1,我们知道,如果存在这么一个\(w_i\),则其他所有石子堆的总异或和为0.
那么先手取走这一堆,就赢了。
反之,如果不存在这么一个\(w_i\) ,则后手必胜。不在存在其他情况.
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
const int N=122300<<2;
#define int long long
#define W cout<<"Win"<<endl
#define G cout<<"Lose"<<endl
#define Croll(i,l,r) for(int i=l;i<=r;++i)
//////////
int n,w[N],add;
//////////
il int read();
void Wonder_of_U();
//////////
main()
{
#ifdef ONLINEJUDGE
freopen("inn","r",stdin);
freopen("outt","w",stdout);
#endif
n=read();
if(n%2){W;return 0;}
Croll(i,1,n)
add^=(w[i]=read());
Croll(i,1,n)
if(add==w[i])
{W;return 0;}
G;
}
il int read()
{
int f=1,x=0;char w=getchar();
while(w<'0'||w>'9')
{if(w=='-')f=-1;w=getchar();}
while(w>='0'&&w<='9')
{x=(x<<3)+(x<<1)+(w^48);w=getchar();}
return f*x;
}
2.[ARC143C] Piles of Pebbles
先强调两个点:只能取\(X\)和\(Y\)个,不能多不能少;可以在一回合取多堆石子。
首先可以预处理一下,给所有的\(w_i\)都对\(x+y\)取模。
这个是显然的,取完模结果不会变。
因为当\(w_i>(X+Y)\)时,每当先手取完若干堆中的\(X\),后手就能立即模仿先手,取这几堆中的\(Y\).所以取模对结果无影响。
取完模后,我们易得,如果没有\(w_i>X\),则先手必输——因为他已经没得取了。
那么剩下的就是存在\(w_i>X\)了。
我们把剩下的再分成两种情况:\(X>Y\)和\(X \leq Y\).
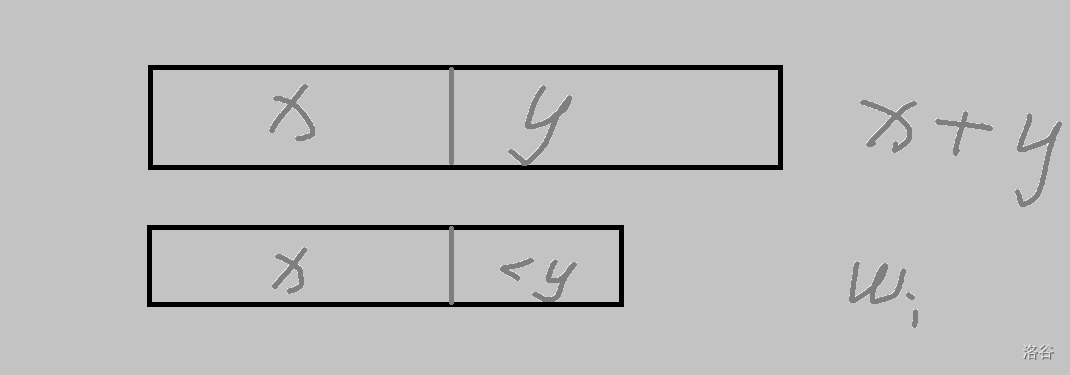
当\(X \leq Y\)时,先手必胜。也很好想。
此时,\(\forall w_i<(X+Y)\)
那么先手者可以取掉剩下所有大于\(X\)的\(w_i\)中的\(X\)。
在这之后,后手就取不了了——因为此时所有\(w_i\)均小于\(Y\).
就像这样。
当\(X>Y\)时,需要判断。
如果存在特殊的\(w_i\)使得$y \leq w_i < x $,
此时这个\(w_i\),后手能取但先手不能,
所以一旦存在这种\(w_i\),则先手必输.反之先手必胜.
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
const int N=122300<<1;
#define int long long
#define Fw cout<<"First"<<endl
#define Sw cout<<"Second"<<endl
#define Croll(i,l,r) for(int i=l;i<=r;++i)
//////////
int w[N];
int n,x,y;
bool tag;
//////////
il int read();
void Wonder_of_U();
//////////
main()
{
#ifdef ONLINEJUDGE
freopen("inn","r",stdin);
freopen("outt","w",stdout);
#endif
n=read();x=read();y=read();
Croll(i,1,n)
{
w[i]=read()%(x+y);
if(w[i]>=x)tag=1;
}
if(!tag)Sw;
else if(x<=y)Fw;
else
{
Croll(i,1,n)
if(w[i]>=y&&w[i]<x)
{Sw;return 0;}
Fw;
}
}
il int read()
{
int f=1,x=0;char w=getchar();
while(w<'0'||w>'9')
{if(w=='-')f=-1;w=getchar();}
while(w>='0'&&w<='9')
{x=(x<<3)+(x<<1)+(w^48);w=getchar();}
return f*x;
}