20230812比赛
T1 【NOIP2014模拟】逻辑的连通性
Description
假如有命题p 一定能推出命题q,则称p 是q 的充分条件,q 是p 的必要条件。
特别的,当p 既是q 的充分条件,又是q 的必要条件时,称p 和q 互为充要条件
现在有n 个命题,其中一些是另一些的充分条件。请问有多少对命题互为充要条件?Input
第一行三个正整数n,m,分别表示命题数、已知关系数
接下来m 行,每行两个正整数p 和q,表示命题p 是命题q 的充分条件Output
仅一行,一个整数,表示充要条件的对数
Sample Input
5 5 1 3 3 2 2 1 4 5 5 4Sample Output
4 样例说明: 4 对充要条件分别是(1, 2)、(2, 3)、(1, 3)、(4, 5)Data Constraint
对于10% 的数据,n <= 10;m <= 50
对于40% 的数据,n <= 500;m <= 1000
对于另外10% 的数据,数据中保证没有重边且m = n^2
对于100% 的数据,n<= 50000;m <= 600000
就是一个强连通分量,对于大小为 \(n\) 的强连通分量,它的充要条件数量为 \(C^2_n=\frac{n(n-1)}{2}\) 。
用 Tarjan 过了。
#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
ll head[600010];
ll nxt[600010];
ll to[600010];
ll cnt;
ll ans;
void addEdge(ll u, ll v) {
cnt++;
to[cnt] = v;
nxt[cnt] = head[u];
head[u] = cnt;
}
ll dfn[50010];
ll col[50010];
ll co[50010];
ll ct[600010];
ll top;
ll cover;
ll num;
ll n, m;
void tarjan(ll u) {
dfn[u] = ++num;
col[u] = num;
ct[++top] = u;
for(ll i = head[u]; i; i = nxt[i]) {
ll v = to[i];
if(!dfn[v]) {
tarjan(v);
col[u] = min(col[u], col[v]);
}
else if(!co[v]) {
col[u] = min(col[u], dfn[v]);
}
}
if(dfn[u] == col[u]) {
co[u] = ++cover;
ll cnt = 1;
while(ct[top] != u) {
co[ct[top]] = cover;
top--;
cnt++;
}
ans += cnt * (cnt - 1) / 2;
top--;
}
}
int main() {
scanf("%lld %lld", &n, &m);
for(ll i = 1; i <= m; i++) {
ll u, v;
scanf("%lld %lld", &u, &v);
if(u != v) addEdge(u, v);
}
for(ll i = 1; i <= n; i++) {
if(!dfn[i]) {
tarjan(i);
}
}
/*=======================Debug Begin=========================*/
// for(ll i = 1; i <= n; i++) {
// printf("id:%lld co:%lld\n", i, co[i]);
// }
/*=======================Debug Finish========================*/
printf("%lld", ans);
}
T2 【NOIP2014模拟】树的连通性
Description
给定一个n 个点的无向图,保证联通且无环无重边,每个点上有一个可修改的权值,每次断掉一条边、修改某个节点上的权值或询问两个点之间的连通性。
Input
输入数据的第一行是两个数N、M,点的个数和操作的个数
接下来N 行,每行一个正整数,表示每个点上的初始权值
接下来若干行,每行两个数x 和y,表示x 和y 之间有一条无向边
接下来M 行,每行三个数t x y,含义如下:
t=1 将x 和y 之间的边断开(保证存在)
t=2 查询x 和y 是否联通,若联通,输出他们权值的乘积,否则输出他
们权值的和
t=3 将点x 上的权值修改为y
为了保证算法强制在线,设上一次查询的结果为lastans,则最后M 行输入
数据的x 和y 的实际值= 输入值xor lastans, lastans 的初始值为0Output
对于每个查询操作,输出一行一个数,要求如上所示
Sample Input
8 5 1 2 3 4 5 6 7 8 1 2 1 5 4 2 3 2 5 7 5 6 8 5 1 5 1 2 4 6 2 11 9 3 0 15 2 0 11Sample Output
10 3 20 样例说明: 先断开1 和5 之间的边,然后查询4 和6 的连通性。由于不联通,所以答案是10 然后查询1 和3 的连通性,由于联通,所以答案是3 然后将3 号节点上的数值修改为12 最后查询3 和8 的连通性。由于不联通,所以答案是它们的权值和20Data Constraint
对于10% 的数据,没有断边操作
对于40% 的数据,n<=1000; m<= 500
对于100% 的数据,n <= 200000; m <= 200000,0 < 点上的权值 <=1000
我暴力过的,正解不是我。
我们使用前向星连边,认较小的为爹。跑 dfs 标记深度,然后对于删边操作,就直接把儿子的父亲标为自己(不用更新深度,因为查询时发现找到子树的根节点了,就是两个点不连通),对于查询联通操作,直接判断哪个边深度小,深度小的边向上爬(如果深度一样随便一个爬),直到两个点重合为止。如果找到根节点(包括子树的根节点),就结束,不连通。
对于修改权值操作,直接改。
#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
ll n, m;
struct node {
ll val;
ll fa;
ll dep;
} a[200010];
ll head[600010];
ll nxt[600010];
ll to[600010];
ll cnt;
ll lastans;
void addEdge(ll u, ll v) {
cnt++;
to[cnt] = v;
nxt[cnt] = head[u];
head[u] = cnt;
}
bool query(ll u, ll v) {
while(u != v) {
if(a[u].dep > a[v].dep) swap(u, v);
if(a[v].fa == v) return false;
v = a[v].fa;
}
return true;
}
void dfs(ll u) {
for(ll i = head[u]; i; i = nxt[i]) {
ll v = to[i];
a[v].dep = a[u].dep + 1;
dfs(v);
}
}
int main() {
scanf("%lld %lld", &n, &m);
for(ll i = 1; i <= n; i++) {
scanf("%lld", &a[i].val);
}
for(ll i = 1; i < n; i++) {
ll u, v;
scanf("%lld %lld", &u, &v);
if(u > v) swap(u, v);
addEdge(u, v);
a[v].fa = u;
}
a[1].fa = 1;
a[1].dep = 1;
dfs(1);
for(ll i = 1; i <= m; i++) {
ll op, x, y;
scanf("%lld %lld %lld", &op, &x, &y);
x ^= lastans;
y ^= lastans;
if(op == 1) {
if(x > y) swap(x, y);
a[y].fa = y;
} else if(op == 2) {
if(query(x, y)) {
lastans = a[x].val * a[y].val;
printf("%lld\n", a[x].val * a[y].val);
} else {
lastans = a[x].val + a[y].val;
printf("%lld\n", a[x].val + a[y].val);
}
} else {
a[x].val = y;
}
}
}
T3 【NOIP2014模拟】图的连通性
Description
“有一个无向图,每次断掉一条边,并询问两个点时候联通,你会维护么?
” 琼很认真地问。
“为什么要知道这个呢?”
“我们总要知道自己是否身陷囹囵……你必须立刻告诉我答案哦”Input
测试数据的第一行是三个正整数n、m、t, 表示无向图有n 个点,m 条边和t 个操作
接下来m 行,每行两个正整数x、y,表示x 和y 之间有一条边(允许存在重边)
接下来t 行,每行三个整数w x y,w=1 时表示将x 和y 之间的边剪断(保证存在这样一条边)。w=2 时表示查询x 与y 时候联通,是输出1, 否则输出0。
为了保证强制在线,最后t 行输入数据中的x 和y 必须要异或(C/C++ 中的^ 运算,PASCAL 中的xor)执行当前操作之前图中剩余的边数,才能得到实际问题中的x 和yOutput
对于每次询问,输出一行,一个数,1 或0,1 表示联通,0 表示不联通。
Sample Input
5 9 6 1 2 2 3 1 3 1 3 3 1 1 5 1 4 3 5 5 4 1 12 13 2 13 12 1 9 12 2 3 2 1 4 6 2 7 5Sample Output
1 0 1 样例说明: 6 个操作依次为: 1. 断掉5 和4 之间的边 2. 查询5 和4 之间的连通性 3. 断掉1 和4 之间的边 4. 查询5 和4 之间的连通性 5. 断掉1 和3 之间的边 6. 查询1 和3 之间的连通性Data Constraint
对于40% 的数据,n <=100; m<=1000; t<=500
对于100% 的数据,n<=100000; m<=150000; t<=100000Hint
关于操作w=1将x 和y 之间的边剪断是删掉一条边.
被坑了QWQ。
比赛时想到了正解,但是以为要在线。其实是强制离线。因为当前操作之前图中剩余的边数,可以很容易算出来。我们用并查集,既然并查集删边难,那我们就让时光倒流,先处理出最后局面,对于删边操作,就连边,对于查询操作,就并查集查询。
然后介绍一个链式前向星取反向边的一种简易的方法,建图时要把cnt置为1,且要保证反向边紧接着正向边建立。则一条id为 \(i\) 边的反向边id为 i^1 。
#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
ll n, m, t;
struct node {
ll val;
} a[200010];
ll fa[200010];
ll head[600010];
ll nxt[600010];
bool go[600010];
ll to[600010];
ll cnt = 1;
ll ans[600010];
ll last;
struct op {
ll w, x, y;
} q[100010];
void addEdge(ll u, ll v) {
cnt++;
to[cnt] = v;
go[cnt] = 1;
nxt[cnt] = head[u];
head[u] = cnt;
}
void delEdge(ll u, ll v) {
for(ll i = head[u]; i; i = nxt[i]) {
ll y = to[i];
if(y == v && go[i]) {
go[i] = 0;
go[i^1] = 0;
break;
}
}
}
ll find(ll x) {
if(fa[x] == x) return fa[x];
return fa[x] = find(fa[x]);
}
int main() {
// freopen("graph4.in", "r", stdin);
// freopen("graph.out", "w", stdout);
scanf("%lld %lld %lld", &n, &m, &t);
ll last = m;
for(ll i = 1; i <= n; i++) fa[i] = i;
for(ll i = 1; i <= m; i++) {
ll u, v;
scanf("%lld %lld", &u, &v);
addEdge(u, v);
addEdge(v, u);
}
for(ll i = 1; i <= t; i++) {
ll w, x, y;
scanf("%lld %lld %lld", &w, &x, &y);
x ^= last;
y ^= last;
q[i].x = x;
q[i].y = y;
q[i].w = w;
if(w == 1) {
delEdge(x, y);
last--;
}
}
for(ll u = 1; u <= n; u++) {
for(ll j = head[u]; j; j = nxt[j]) if(go[j]) {
ll v = to[j];
ll x = find(u);
ll y = find(v);
fa[x] = y;
}
}
for(ll i = t; i >= 1; i--) {
if(q[i].w == 1) {
ll x = find(q[i].x);
ll y = find(q[i].y);
fa[x] = y;
} else {
ans[i] = (find(q[i].x) == find(q[i].y));
}
}
for(ll i = 1; i <= t; i++) {
if(q[i].w == 2) {
printf("%d\n", ans[i]);
}
}
}
T4 【NOIP2019模拟11.07】极好的问题
Description
Input
从文件 awesome.in 中读入数据。
第一行 2 个用空格隔开的整数 n, P。
第二行 n 个用空格隔开的整数 A1, . . . , An。Output
输出到文件 awesome.out 中。
输出一行一个整数,表示极好的三元组的数目。Sample Input
Sample Input1 5 5 1 1 1 2 3 Sample Input2 4 5 7 4 2 2Sample Output
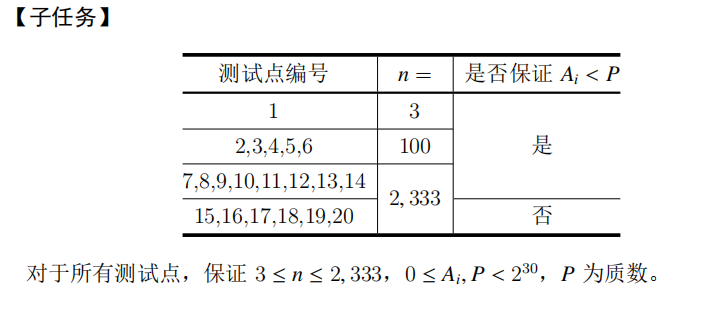
Sample Output1 2 【样例 1 解释】 唯二的极好的三元组为 (1, 1, 1) 和 (1, 2, 3)。 Sample Output2 2 【样例 2 解释】 (2, 2, 4) 和 (2, 4, 7) 都是极好的三元组。Data Constraint
极好的三元组有以下三种情况:
- \(a,a,a\)
- \(a,a,b\)
- \(a,b,c\)
对于第一种情况,可以统计每个出现次数大于等于 3 的数的三次方 (在 模P 意义下) 是否等于 1 。
对于第二种情况,统计每个出现次数大于等于 2 的数的二次方乘去重序列中的其它数 (在 模P 意义下) 是否等于 1
对于第三种情况,预处理出所有两个不同的数的乘积,并在预处理中特判 \(a\times b=a'\) 或 \(a\times b=b'\) 的情况。因为此时等价于情况二,不特判会导致重复计算。然后求出每个数的乘法逆元在这些乘积中出现的次数。这些次数之和会反复出现三次,所以记得除以3。
#include <cstdio>
#include <algorithm>
#include <cstring>
#define ll long long
using namespace std;
ll n, p, ans;
ll a[40000];
ll b[40000];
ll g[40000];
ll inv[40000];
ll an[2334*2334];
void solve(ll l, ll r) {
if(l == r) return;
ll mid = (l + r) >> 1;
solve(l, mid);
solve(mid + 1, r);
ll pos1 = l, pos2 = mid + 1;
for(ll i = l; i <= r; i++) {
if(pos2 > r || (pos1 <= mid && a[pos1]<a[pos2])) {
g[i] = a[pos1++];
}
else {
g[i] = a[pos2++];
}
}
for(ll i = l; i <= r; i++) {
a[i] = g[i];
}
}
ll qpow(ll x, ll y) {
if(y == 0) return 1;
if(y % 2 == 0) {
ll res = qpow(x, y / 2) % p;
return (res % p) * (res % p) % p;
}
return (x % p) * (qpow(x, y - 1) % p) % p;
}
int main() {
freopen("awesome.in", "r", stdin);
freopen("awesome.out", "w", stdout);
scanf("%lld %lld", &n, &p);
for(ll i = 1; i <= n; i++) {
scanf("%lld", &a[i]);
}
a[n + 1] = -114514;
solve(1, n);
memcpy(b, a, sizeof(a));
ll e = unique(b + 1, b + 1 + n) - b - 1;
for(ll i = 1; i <= e; i++) {
inv[i] = qpow(b[i], p - 2);
}
ll last = -1919810, num = 0;
for(ll i = 1; i <= n + 1; i++) {
if(a[i] != last) {
if(num >= 2) {
for(ll j = 1; j <= e; j++) {
if(b[j] != last && ((last % p) % p * (last % p) % p * (b[j] % p)) % p == 1) ans++;
}
}
if(num >= 3) { // 之所以不用else if,因为在num>=2中处理了a*a*b的情况,这里虽然num>=3,但也可以舍去第一个,变成a*a*b
if(((last % p) % p * (last % p) % p * (last % p)) % p == 1) ans++;
}
last = a[i];
num = 1;
} else {
num ++;
}
}
ll tot = 0, res = 0;
for(ll i = 1; i <= e; i++) {
for(ll j = i + 1; j <= e; j++) {
an[++tot] = (b[i] % p) % p * (b[j] % p) % p;
if(an[tot] == inv[i]) res--;
if(an[tot] == inv[j]) res--;
}
}
sort(an + 1, an + 1 + tot);
for(ll i = 1; i <= e; i++) {
ll rig = upper_bound(an + 1, an + 1 + tot, inv[i]) - an;
ll lef = lower_bound(an + 1, an + 1 + tot, inv[i]) - an;
res += rig - lef;
}
printf("%lld", res/3 + ans);
}