静态博弈指的是博弈各方同时做出决策，或者说决策有先后顺序，但是在做决策时博弈者互相看不到其他博弈者的策略，一旦做出决策后就只能等待博弈的结果，其对博弈的发展也不能产生任何影响。静态博弈又称为“同时决策博弈”（Simultaneous Move Games）。静态博弈有很多例子，比如之前介绍的“囚徒困境”、“猜硬币”、“剪刀·石头·布”等。博弈两种表现形式，一种是策略式博弈（Normal Form Game）；另外一种是扩展形式的静态博弈（Extensive Form Game）。一般前者用收益矩阵来表示，后者用树形结构来表示。前面我们探讨了纳什均衡及其存在性的问题，那么如何求解纳什均衡呢？这里继续讨论一些求解纳什均衡的一般方法。

一、划线法

求解纳什均衡最基本的方法是用最优反应函数，在许多博弈问题中，为了图示简单表达，将最佳反应函数用图示方法展现出来，就给出了可视化的划线法和箭头法来求解博弈。
划线法是通过将某个参与人的策略效用两两比较，逐次确定相对优势策略，最终在这种比较中，选择出最优的策略组合。其方法为：在每一个博弈方针对对方每一个策略的最大可能得益下划一条短线，双方的相对优势策略都这样划线以后,如果那个格子里面的两个数字下面都划了短线,这个格子对应的(相对优势)策略组合,就是一个纳什均衡。
以下图博弈\(G\)为例来说明划线法的使用。首先考虑参与人1的策略，当他使用“上”策略时，最大的效用为1，于是我们在他使用“上”策略时收获的两个效用1下各划一道横线；同理，当他使用“下”策略时，最大效用为2，于是在数字2下划线。再考虑参与人2，当他使用“左”策略时，收获的最大效用为4，于是在4下面划线，当他使用“中”策略时，收获的最大效用为3，于是在3下面划线，当他使用“右”策略时，收获的最大效用为1，于是在1下面划线。由此，我们看到，这个博弈矩阵中只有效用组合(1,3)下划了两道线，因此其对应的策略组合{上，中}为均衡解。

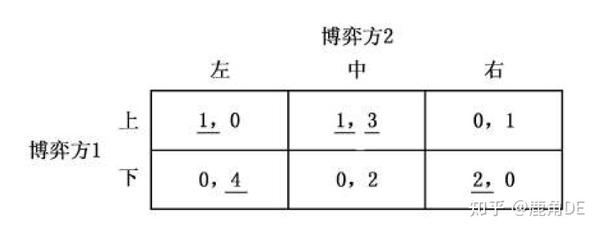
二、箭头法

箭头法的核心思想是：基于当前状况如何能继续将效用最大化。它是对博弈中的每个策略组合进行分析,判断各博弈方是否能够通过单独改变自己的策略而改善自己的得益，如果可以，则从所考察的策略组合的得益引一个箭头到改变策略后的策略组合对应的得益。这样对每个可能的策略组合都分析考察过以后，根据箭头反映的情况来判断博弈的结果。因此箭头法是一种动态的求解方法。一个箭头可以形象地把博弈方的“理性人”本质表示出来，从策略选择的改变带来得益的增加。博弈矩阵中没有箭头指出的格子所代表的策略组合，表示每个博弈方都没有单独改变策略选择的倾向，这个策略组合就是纳什均衡。
以博弈\(G\)为例，来演示箭头法。我们假定目前博弈的策略组合为：{下，左}。此时参与人1的效用为0，那么他可以通过改变策略的方式来提高自己的效用，为此他可以改变选择使用“上”策略，那么我们从组合(0,4)(0,4)(0,4)出发，往组合(1,0)(1,0)(1,0)的方向划箭头，此时的策略组合为：{上，左}，再来分析参与人2，改用“中”策略和“右”策略都可以提高其效用，且同时若采用“右”策略，则他还可以更换“中”策略以使自己的效用更大，因此我们需要划三道箭头。此时的策略为{上，中}。再考虑剩余的情况，如果采用{下，中}，那么双方的效用都只会变小，因此我们只能从(0,2)(0,2)(0,2)向(1,3)(1,3)(1,3)划箭头，依次分析完所有的情况，我们得到下图：

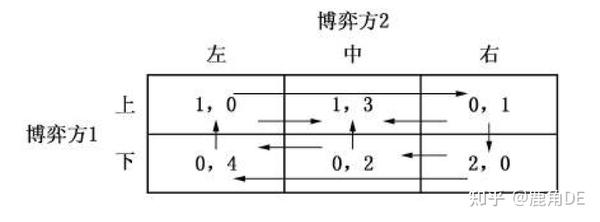
可以发现，只有(1,3)的组合没有被箭头所指出，因此它是一个稳定的策略组合的效用。所以{上，中}为均衡解。

三、严格劣策略消去法

如果在一个博弈中存在“占优策略均衡”，那么自然是好分析的，然而大部分博弈是没有“占优策略均衡”的，我们这里考虑用“严格劣策略消去法”来化简博弈。
该方法的求解过程为：首先找出某个博弈方的严格劣策略，将它删除，然后重新构造不包含这个劣策略的博弈；然后，继续删除新的博弈中某个博弈方的严格劣策略；重复这一个过程直到剩下唯一的策略组合为止，这个策略组合便是博弈的均衡解。
在这里提到的严格劣策略（Strictly Dominated strategies），它指的是某一个博弈中，不管其他博弈者选择什么样的策略，我的“策略”的收益总是比我其他某个策略的收益低，这个“策略”便是严格劣策略。接下来举一个具体的例子来展示严格下策反复消去法求解博弈的过程。假设有一个博弈如下矩阵所示，

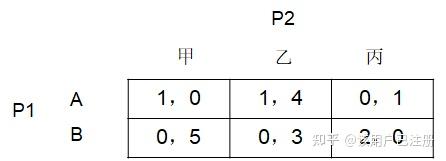
其中，P1（Player1）和P2（Player2）代表两个博弈者，P1有两个策略A和B，P2有三个策略甲、乙、丙。根据收益矩阵不难这个博弈没有“占优策略均衡”，因为P1的两个策略不存在占优策略，P2的三个策略也不存在占优策略。
我们来分析是否可以用严格劣策略消去法。先看P2，如果有严格劣策略，说明不管P1选什么，P2的某个策略收益比P2其他某个策略收益小。我们发现不论P1选“A”还是“B”，P2选择“丙”的收益都比选择“乙”的收益低。因此，策略“丙”是相对于策略“乙”的严格下策，可以将策略“丙”删除，因为P2永远不会选“丙”。新的博弈如下图所示

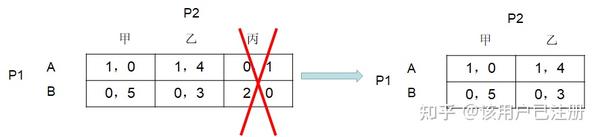
在新的博弈中，P1和P2都只有两个策略，我们再来分析P1，发现无论P2选择“甲”还是“乙”，P1选“B”的收益比选“A”的收益低，也就是“B”是相对于“A”的严格劣策略，因此P1不可能会选择“B”，我们将这个策略删除。新的博弈如下图

可以看到，新的博弈中P1只有“A”这一个策略，P2有“甲”和“乙”两个策略，我们再比较P2的两个策略，发现“甲”是相对于“乙”的严格劣策略，因此我们删掉P2的“甲”策略。于是博弈的最终结果为P1选择“A”，P2选择“乙”。

四、混合策略纳什均衡

以猜硬币博弈为例，每以参与人持一枚硬币，选择出正面或背面向上。若两枚硬币一致（即全部正面向上或背面向上），则参与人2赢走参与人1的硬币；如果两枚硬币不一致（一正一反），则参与人1赢走硬币，博弈的收益矩阵如下图。可以发现在此博弈中不存在前一小节中定义的纯策略纳什均衡，因为无论哪一个状态都有参与者有意愿偏离。

在博弈中，一旦每个参与者都竭尽全力试图猜测其他参与者的策略，就不存在纯策略纳什均衡，因为此时参与者的最优行为是不确定的，而博弈的结果必然要包含这种不确定性。因此，在这里引出混合策略（mixed strategy）。将参与人的每一可能信息集映射到一个关于行动的概率分布上。即参与人在同一种给定的情况下有可能选择集中不同行动中的任何一种。对于参与人\(i\)来讲，参与者\(-i\)的混合策略代表了他对\(-i\)选择策略的不确定性，参与者\(i\)由此计算出他对参与者\(-i\) 的最优反应。

仍以猜硬币博弈为例，参与者1以概率\(p\)出正面，以概率\((1-p)\)背面；参与者2以概率\(p\)出正面，以概率￥(1-p)￥背面。参与者1出正面可得期望收益为

，出背面的期望收益为

。参与者2为了使其策略具有不确定性（即参与者1猜不到他的策略），得让参与者1出正面和出背面的期望收益相等，此时解得

。如果\(q\geq 1/2\)参与者1的最优反应是选择正面（参与者1将会一直选择正面），如果\(q\leq 1/2\)参与者的最优反应是选择背面（参与者2将会一直选择背面），这两种情况都使得参与者2的策略失去了不确定性。因此，参与者2的混合策略为(1/2,1/2)。同理，可以计算得到参与者1的混合策略为(1/2,1/2)。

参与人策略可以用上图表示出，其中的交点为参与者双方的混合战略的纳什均衡。

参考文献

1. 完全信息静态博弈--静态博弈与占优策略均衡
2. 博弈论（Game Theory）入门——完全信息静态博弈
3. 博弈论——完全信息静态博弈4