Tarjan 例题:洛谷P4819 [中山市选] 杀人游戏
在洛谷中查看
前言:
这道题挺好,有很多坑点,锻炼思维,和 Codeforces 的思维题有些相似。
思路:
第一阶段:
很明显,在一个强连通分量里的点都能知道别人是不是杀手。那么就直接找缩完点后有几个入度为 \(0\) 的强连通分量。但这样是 28pts 。
为什么呢?举个栗子。
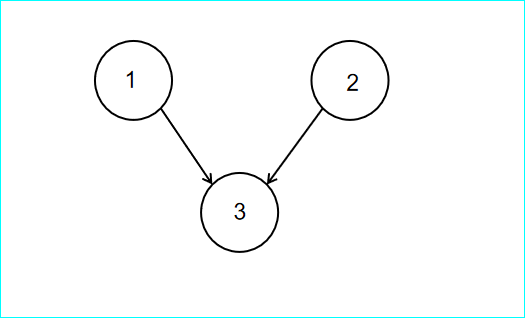
我们直接找点 \(1\),它是杀手的概率为 \(\frac{1}{3}\),我们如果找它,有两种情况:
- 点 \(3\) 是杀手,那就找到了。
- 点 \(3\) 不是杀手,那排除法点 \(2\) 就是杀手,也找到了。
那最终能安全找到的概率就是 \(\frac{2}{3}\) 了,但上面那个思路并没有考虑排除法。
第二阶段:
题解讲得其实很清楚了,只要存在一个点 \(P\),它所有能到的点的入度都大于1(意味着从别的强连通分量也能到那个点),那么这个点 \(P\) 就是可以根据排除法排除的。
错误思路:
我这只说一个错的思路为什么错。可以看看这个思路。
其实自己想象都行,为什么并查集维护不行呢?
因为联通的也可以背排除啊,就上面那个图就是一个反例(一图两用了哈哈)。
Code:
所以其实并没有什么要将的了,只是我思路错了,给个代码吧~
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+5;
int n,m,dfn[N],low[N],num,cnt,col[N],st[N],top,du[N],val[N],new_val[N];
bool vis[N];
vector<int> g[N],new_g[N];
map<string,int> cur;
inline int read(){
int s=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){s=(s<<1)+(s<<3)+(c^48);c=getchar();}
return s*f;
}
void tarjan(int x){
dfn[x]=low[x]=++num;st[++top]=x;
for(int i=0;i<g[x].size();i++){
int t=g[x][i];
if(!dfn[t])tarjan(t),low[x]=min(low[x],low[t]);
else if(!col[t])low[x]=min(low[x],dfn[t]);
}
if(dfn[x]==low[x])for(cnt++;st[top+1]!=x;top--)col[st[top]]=cnt,new_val[cnt]++;
}
int main(){
n=read();m=read();
for(int i=1;i<=n;i++)val[i]=1;
for(int i=1;i<=m;i++){
int u=read(),v=read();
g[u].push_back(v);
}
for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i);
for(int i=1;i<=n;i++){
for(int j=0;j<g[i].size();j++){
int t=g[i][j];
if(vis[col[t]])continue;
vis[col[t]]=true;
if(col[i]!=col[t])new_g[col[i]].push_back(col[t]),du[col[t]]++;
//一定注意同个强连通分量不能连重边,所以要打标记
}
for(int j=0;j<g[i].size();j++)vis[col[g[i][j]]]=false;
}
int ans=0;
bool flag=0;
for(int i=1;i<=cnt;i++){
if(!du[i])ans++;
if(!du[i]&&new_val[i]==1&&!flag){//只有一个点时才能用排除法哦
bool mark=1;
for(int j=0;j<new_g[i].size();j++){
int t=new_g[i][j];
if(du[t]<2)mark=0;
}
if(mark)flag=1,ans--;//如果能到的点都能由别的强连通分量过来,那么这个点就能用排除法排除。
}
}
printf("%.6lf",(n-ans)*1.0/n);
return 0;
}