二项式定理与杨辉三角

LDUyanhy / 2023-08-11 / 原文

杨辉三角

$1.$杨辉三角计算公式

组合公式 $ C_{n}^{r} $ = $ n $ !/ $ r $ ! $ (n - r) $ !。把 $ C_{n}^{r} $ 称为二项式系数。杨辉三角是二项式系数的典型应用：

仔细发现，可以得到：杨辉三角第 $ i $ 层上的数，是 $(1 + x)^i $ 展开后各项的系数。

推导得： $ (a + b)^n = \Sigma_{r = 0}^{n} C_{n}^{r} a^r b^{n - r} = \Sigma_{r = 0}^{n} C_{n}^{r} b^r a^{n - r} $，这个公式称为二项式定理。

当 $ n $ 较大，需要取模时，二项式系数有两种计算方法。

$(1).$利用递推公式：$ C_{n}^{r} = C_{n - 1}^{r} + C_{n - 1}^{r - 1} $。

$(2).$用逆元直接计算。

下面给出这两种思路的实现代码：

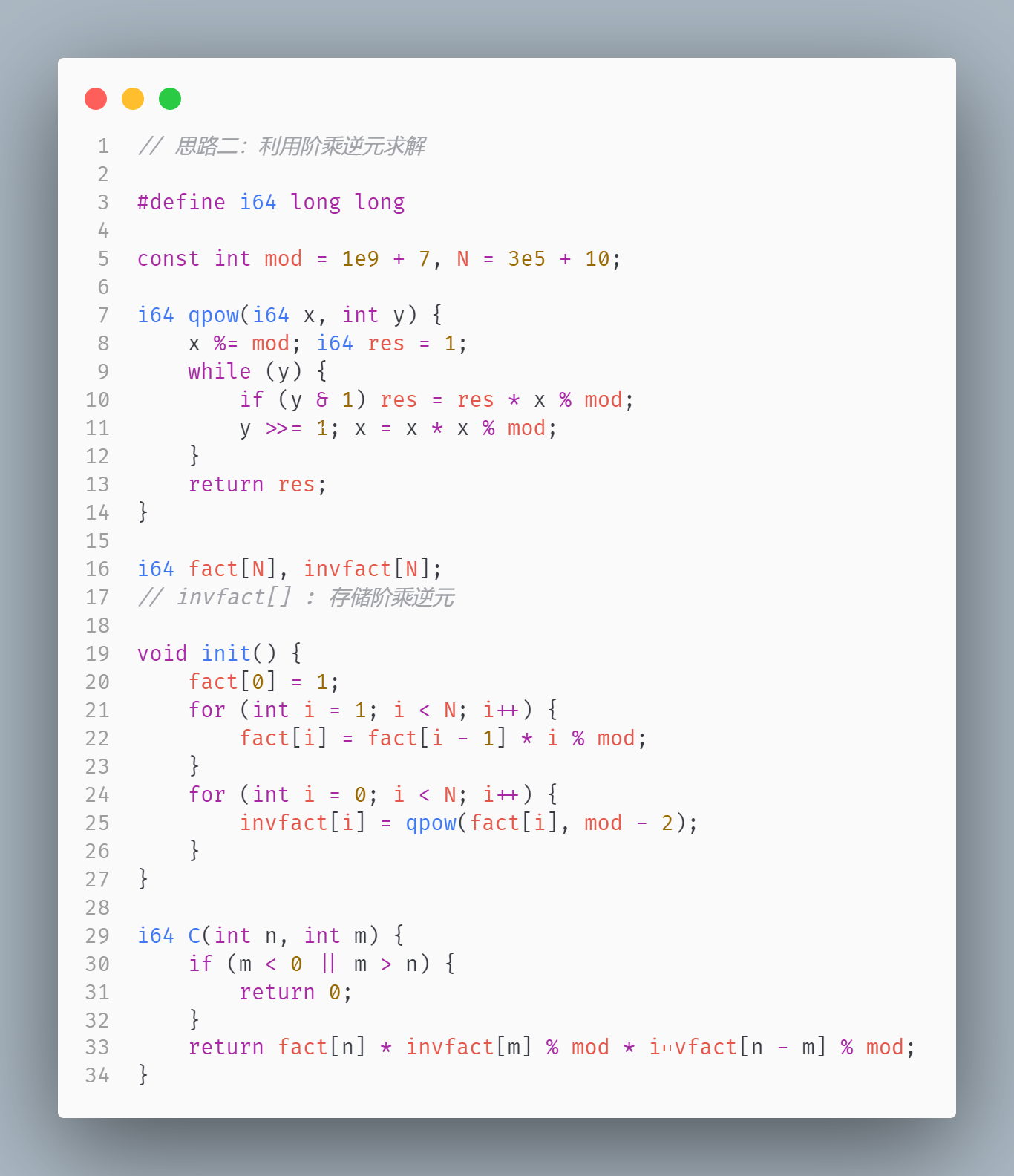
这里可以进行一些小优化，因为 $ 1/fact[i] = (i + 1)/fact[i + 1] $，所以，$ invfact[i] = (i + 1) \times invfact[i + 1] $。因此，求逆元的过程可以改写成如下形式：(先求出最后一项的逆元，然后逆推计算前面的项的逆元)。

P1313 [NOIP2011 提高组] 计算系数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

$ x^n \times y^m $ 项的系数是：$ C_{k}^{n} a^n b^{k - n} $。直接计算该式子即可。

#include <bits/stdc++.h>
#define L(i, j, k) for (int i = (j); i <= (k); ++i)
#define R(i, j, k) for (int i = (j); i >= (k); --i)
#define i64 long long
#define LL unsigned long long
#define pii std::pair<int, int>

inline int read() {
    bool sym = false; int res = 0; char ch = getchar();
    while (!isdigit(ch)) sym |= (ch == '-'), ch = getchar();
    while (isdigit(ch)) res = (res << 3) + (res << 1) + (ch ^ 48), ch = getchar();
    return sym ? -res : res;
}

// 思路一: 利用递推式处理
const int N = 2200, mod = 10007; // 模数
i64 C[N][N];
/* 用递推法计算时, 需要注意两个地方：
    1. 边界为 C[0][0] = 1;
    2. C[i][0] = 1; (防止当 j = 0时, j - 1 越界)
*/

void init() {
    C[0][0] = 1;
    for (int i = 1; i <= N - 1; i++) {
        C[i][0] = 1;
        for (int j = 1; j <= i; j++) {
            /* 算法竞赛中认为, 当 r > n 时, C[n][r] = 0 */
            C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % mod;
        }
    }
}

i64 qpow(int x, int y) {
    x %= mod; i64 res = 1;
    while (y) {
        if (y & 1) res = res * x % mod;
        y >>= 1; x = x * x % mod;
    }
    return res;
}

int main() {
    init();
    int a = read(), b = read(), k = read(), n = read(), m = read();
    printf("%lld\n", C[k][n] * qpow(a, n) * qpow(b, m) % mod);
    return 0;
}

P2822 [NOIP2016 提高组] 组合数问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

因为 $ k $ 是固定的, 所以不难想到的一个思路是, 通过观察 $ C_{i}^{j} $ 模 $ k $ 是否为 $ 0 $ 来判断 $ C_{i}^{j} $ 是否是 $ k $ 的倍数 (即计算组合数时，对 $ k $ 取模), 为了避免重复进行不必要的计算, 我们采用二维前缀和优化, 总的时间复杂度为 $ O(n^2) $。

#include <bits/stdc++.h>

#define i64 long long

inline int read() {
    bool sym = false; int res = 0; char ch = getchar();
    while (!isdigit(ch)) sym |= (ch == '-'), ch = getchar();
    while (isdigit(ch)) res = (res << 3) + (res << 1) + (ch ^ 48), ch = getchar();
    return sym ? -res : res;
}

const int N = 2e3 + 100;

i64 C[N][N];
i64 sum[N][N];
int k;

int main() {
    int t = read(), k = read();
    C[0][0] = 1;
    for (int i = 1; i <= 2000; i++) {
        C[i][0] = 1;
        for (int j = 1; j <= i; j++) {
            C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % k;
        }
    }
    for (int i = 0; i <= 2000; i++) {
        for (int j = 0; j <= i; j++) {
            sum[i][j] = (C[i][j] == 0);
        }
    }
    for (int i = 1; i <= 2000; i++) {
        for (int j = 1; j <= 2000; j++) {
            sum[i][j] = (sum[i - 1][j] + sum[i][j] + sum[i][j - 1] - sum[i - 1][j - 1]);
        }
    }

    while (t--) {
        int n = read(), m = read();
        printf("%lld\n", sum[n][m]);
    }
    return 0;
}