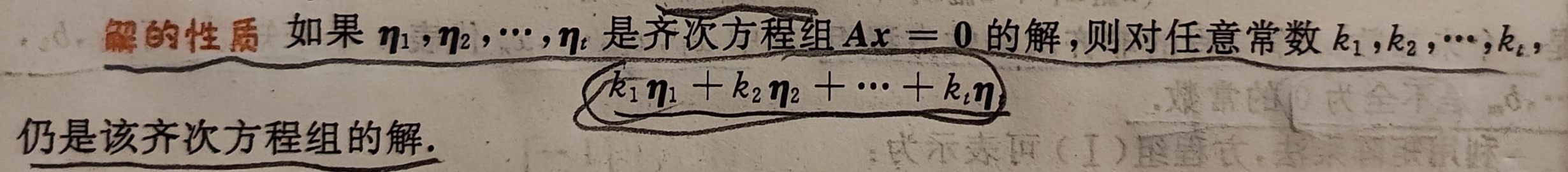【线性代数】线性方程组 1.基本概念
1.线性方程组的基本概念
齐次/非齐次线性方程组的概念在高数中已经涉及过了。

非齐次线性方程组就是方程组右侧的常数不全为0的线性方程组。
非齐次线性方程组还可以用矩阵形式和向量形式表示出来。

齐次线性方程组的情况是类似的,只是右侧的常数全为0。
矩阵形式和向量形式也是类似,只是右侧结果为零矩阵和零向量。
方程组的解:
将方程组I或II中的未知数Xi用常数代替使方程组满足,则称这些常数组成的向量是方程组的一个解。
注意,方程组的解应该是一个向量或矩阵。
解方程组的一般过程:
解方程组就是找出所有能使方程组成立的解。

2.齐次线性方程组
关于齐次线性方程组的解:
对于齐次线性方程组,由于方程的右侧都是0,所以零向量一定是齐次线性方程组的解,称为零解。
解齐次线性方程组一般都是求方程组的非零解。
基础解系的定义:
如果齐次线性方程组的解满足以下两个条件:
(这里说的是一系列方程组的解组成的向量组)
(1)这个向量组线性无关
(2)这个方程组的任意一个解都可以由这个向量组线性表出
则称这个解向量组称为齐次线性方程组的一个基础解系。
齐次线性方程组的解有这样的性质:
这个性质很好理解,因为齐次线性方程组的等号右边是0,无论将多少个解代入方程组或乘上系数并相加,等号右边仍然是0,所以这个线性表示仍是方程组的解。
齐次方程组的解与其系数矩阵的秩之间的关系:

1.r(A) < n代表这些系数向量是线性相关的,有多余出来的能被其他向量线性表出的系数向量。
2.m < n代表系数向量的维数为n,而系数向量的数量有m个,多于n。而最多只能有n个n维向量之间线性无关,所以一定会有剩下的至少m-n个系数向量(还可能比这个多)能被其他最多n个线性表出,所以此时齐次线性方程组必有非零解。
3.m=n时,只有当系数矩阵的行列式为0,即系数向量组线性相关,才能使齐次线性方程组有非零解。否则的话就是这n个向量之间线性无关,相互独立,只有所有未知数都等于0才能使方程组成立。
4.这里乍一看会很困惑,但是其实这里说的是解的线性无关性,而不是系数向量的。
3.非齐次线性方程组
其求解的过程和齐次线性方程组是一样的,也是做同解变形直到求出解。