模拟赛做到的题，赛后看了 Y2hlbnlpa2Fp 的题解，感觉没讲清楚，这里做下补充，提供自己的理解。

基本思路：

对每个 \(A_i\) 的答案进行预处理，对于每个询问，只需要找到第一个到达的景点即可。

那么如何预处理每个点的答案呢？有一条很重要的性质：最多转向 \(\log{X}\) 次。

要证明这个结论，先放上一张图：

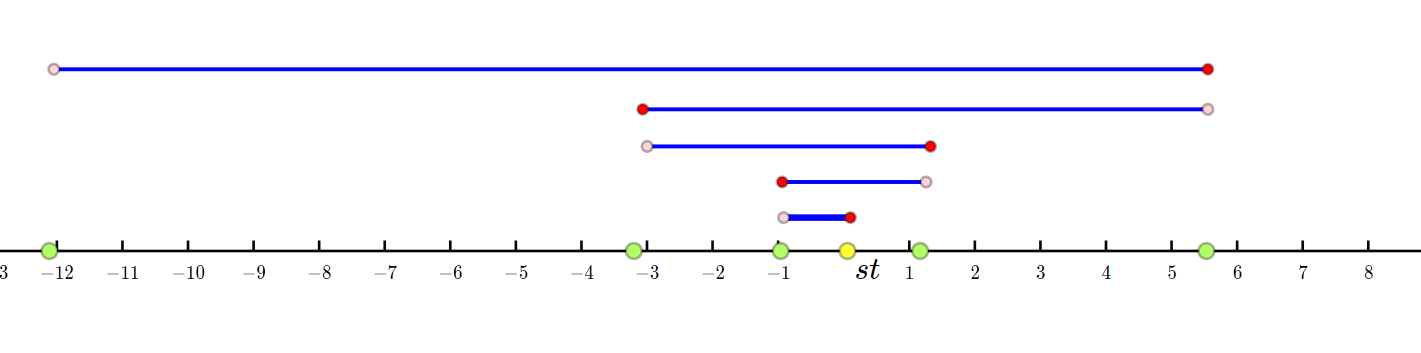
设第 \(k\) 段路径长度为 \(L\)，从图中可以看出，\(L_{k}\geq 2\times L_{k-1}\)，因为 \(1 \leq L_k\leq X\)，可以推得 \(k\leq \log{X}\)。

证明了这个结论，我们就可以在 \(\mathcal{O}(n^2\log{n})\) 的时间暴力走一遍预处理出答案，运用ST表倍增可以优化到 \(\mathcal{O}(n\log^2{n})\)。

对于每个询问，二分找到第一个到达的景点，直接输出对应的答案即可。

整体复杂度 \(\mathcal{O}(n\log^2{n}+q\log{N})\)。

注释很详细，写在代码里，注释掉的代码是对 Y2hlbnlpa2Fp 题解的改进。

\(Code\)

#include<bits/stdc++.h>//MoSheng
using namespace std;
#define ll long long
#define ul unsigned long long
#define db double
#define il inline
#define re register
#define INF 0x3f3f3f3f
#define LINF 0x3f3f3f3f3f3f3f3f//ll范围下LINF，够大 
#define int ll//要开longlong 
#define F(i,a,b) for(int (i)=(a);(i)<=(b);(i)++)
#define DF(i,a,b) for(int (i)=(a);(i)>=(b);(i)--)
#define G(i,u) for(int (i)=head[u];(i);(i)=nxt[(i)])
inline ll read(){ll x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-48;ch=getchar();}return x*f;}
const int N=200010;
int n;
int pos[N],ans[N];
int stl[N][25],str[N][25];
signed main()
{
	n=read();
	F(i,1,n) pos[i]=read();
	pos[0]=-LINF;//边界处理I
	pos[n+1]=LINF;//一定要开7f^4或3f^8，1e9范围下3f^4太小 
//	if(n==1)//特判？其实没必要，因为有边界处理 
//	{
//		int q=read();
//		F(i,1,q)
//		{
//			int loc=read();
//			printf("%lld\n",abs(loc-pos[1]));
//		}
//		return 0;
//	}
	F(i,1,n-1) stl[i][0]=pos[i]-(pos[i+1]-pos[i]);//该点向右移动的距离在左边的坐标映射，便于与左节点距离比较 
	stl[n][0]=-LINF;//边界处理II
	F(i,2,n) str[i][0]=pos[i]+(pos[i]-pos[i-1]);//该点向左移动的距离在右边的坐标映射，便于与右节点距离比较 
	str[1][0]=LINF;
	F(k,1,20)
	{
		F(i,1,n)
			if(i+(1<<(k-1))<=n)
				stl[i][k]=min(stl[i][k-1],stl[i+(1<<(k-1))][k-1]);//过程中最远的一次能满足就一定满足全过程，所以取极值 
//			else//不满足则说明扩展到底了，不用继续拓展。但其实这步不需要，因为处理时不满足时会continue 
//				stl[i][k]=stl[i][k-1];
		F(i,1,n)//DF(i,n,1)//正反皆可 
			if(i-(1<<(k-1))>=1)
				str[i][k]=max(str[i][k-1],str[i-(1<<(k-1))][k-1]);
//			else
//				str[i][k]=str[i][k-1];
	}
	F(i,1,n)
	{
		int l=i,r=i,dir=0,now=i;//l和r分别表示左右两边走到的最远点 
		if(pos[i]-pos[i-1]<=pos[i+1]-pos[i]) dir=0;//判断开始时移动方向，0为左，1为右  
		else dir=1; 
		while(1<l||r<n)//还有没走的点 
		{
			if(dir==0)//先向左再向右转 
			{
				now=l;
				now--;//转完向至少走一步，提前走掉 
				DF(k,20,0)//倍增经典倒序，向左走到不能走 
				{
					if(now-(1<<k)<1) continue;//无法往左移动1<<k次就跳过，注意不能带= 
					if(str[now][k]<=pos[r+1]) now-=(1<<k);//向左走的距离更近就走，注意这里now不需要-1，因为我们已经提前走过一步了 
				}
//				now--;//这一步与now的-1一样，其实就是上一次转向后至少要走的那一步，我们在转向后立刻处理就不需要（不能加）这一步 
				ans[i]+=pos[r]-pos[now];
				l=now;
				dir=1;//记得转向 
			}
			else// if(dir==1)//先向右再向左转 
			{
				now=r;
				now++;//转完向至少走一步，提前走掉 
				DF(k,20,0)//倍增经典倒序，向右走到不能走 
				{
					if(now+(1<<k)>n) continue;//无法往右移动1<<k次就跳过，注意不能带=
					if(stl[now][k]>pos[l-1]) now+=(1<<k);//向右走的距离更近就走，与dir==0的情况同理，now不需要+1 
				} 
//				now++;//与dir==0的情况同理，这步不加 
				ans[i]+=pos[now]-pos[l];
				r=now;
				dir=0;//记得转向 
			}
		}
	}
	int q=read();
	F(i,1,q)
	{
		int loc=read();
		int R=upper_bound(pos+1,pos+n+1,loc)-pos;//找右边最近点，lower_bound和upper_bound都可 
		int L=R-1;//左边最近点 
		if(loc-pos[L]<=pos[R]-loc) printf("%lld\n",loc-pos[L]+ans[L]);
		else printf("%lld\n",pos[R]-loc+ans[R]);
	}
	return 0;
}