李超树
李超数支持动态插入线段/直线,查询单点极值。
算法思想
排除不可能成为最优解的,维护在当前区间能成为最优解的线段,即该线段在当前区间的某个取值上有最优解。
查询的时间复杂度是 \(O(\log n)\) 的,修改时通过替换和下放,也能达到 \(O(\log n)\) 的复杂度,区间修改能达到 \(O(\log^2 n)\),(证明:最多把每条直线的值域分到 \(\log n\) 个区间,每个区间最多把标记下传 \(\log n\)层,所以区间修改的复杂度为 \(O(\log ^2 n\))。
对信息进行维护时,可以使用斜率和线段的中点取值进行分类讨论。( \(eg\) :
(在类似于这样的图上面插入新线段
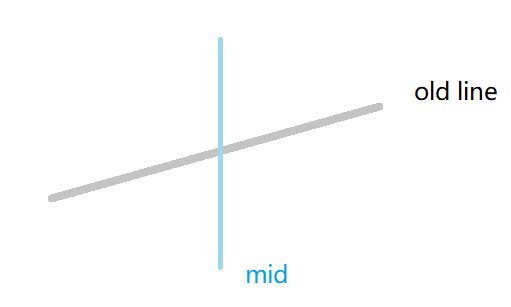
设当前区间为 \([L,R]\) ,当前区间的中点为 \(mid\)。
-
当前区间没有线段,新鲜段直接放入该区间。
-
新线段的斜率小于旧线段的斜率:
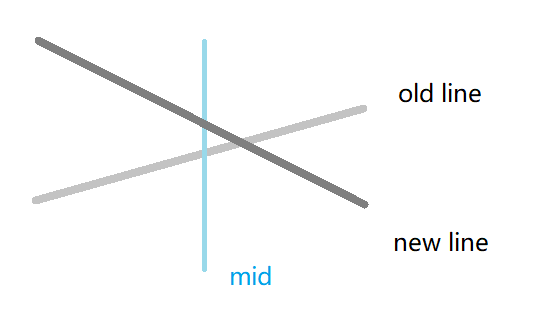
- 若新线段在中点处的取值 \(>\) 旧线段的取值,则新线段在 \([L,mid]\) 上的取值一定比旧线段更优,但旧线段可能在 \([mid+1,R]\) 上的取值更优,用新线段替换当前节点的旧线段,将旧线段下放至 \([mid+1,R]\) 区间并递归更新答案。
- 若新线段在中点处的取值 \(<\) 旧线段的取值,则旧线段在 \([mid+1,R]\) 上的取值一定比新线段更优,但新线段可能在 \([L,mid]\) 上的取值更优,将新线段下放至 \([L,mid]\) 区间并递归更新答案。
-
新线段的斜率大于旧线段的斜率:
- 若新线段在中点处的取值 \(>\) 旧线段的取值,则新线段在 \([mid+1,R]\) 上的取值一定比旧线段更优,但旧线段可能在 \([L,mid]\) 上的取值更优,用新线段替换当前节点的取值,将旧线段下放至 \([L,mid]\) 区间并递归更新答案。
- 若新线段在中点处的取值 \(<\) 旧线段的取值,则旧线段在 \([L,mid]\) 上的取值一定比新线段更优,但新线段可能在 \([mid+1,R]\) 上的取值更优,将新线段下放至 \([mid+1,R]\) 区间并递归更新答案。
-
新旧线段斜率相同,则比较截距 \(b\),截距大的取值更优,直接用截距大的。