博弈论概述——博弈的要素和分类(一)
博弈论是现代数学的一个新分支,也是运筹学的一个重要学科。它主要研究公式化了的激励结构间的相互作用,是研究具有斗争或竞争性质现象的数学理论和方法。博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。博弈论已经成为经济学的标准分析工具之一,在金融学、证券学、生物学、经济学、国际关系、计算机科学、政治学、军事战略和其他很多学科都有广泛的应用。
一、博弈实例
1.1 囚徒困境
故事讲的是,两个嫌疑犯作案后被警察抓住,分别关在不同的屋子里接受审讯。警察知道两人有罪,但缺乏足够的证据。警察告诉每个人:如果两人都抵赖,各判刑一年;如果两人都坦白,各判八年;如果两人中一个坦白而另一个抵赖,坦白的放出去,抵赖的判十年。于是,每个囚徒都面临两种选择:坦白或抵赖。然而,不管同伙选择什么,每个囚徒的最优选择是坦白:如果同伙抵赖、自己坦白的话放出去,不坦白的话判一年,坦白比不坦白好;如果同伙坦白、自己坦白的话判八年,不坦白的话判十年,坦白还是比不坦白好。结果,两个嫌疑犯都选择坦白,各判刑八年。如果两人都抵赖,各判一年,显然这个结果好。但这个帕累托改进办不到,因为它不能满足人类的理性要求。囚徒困境所反映出的深刻问题是,人类的个人理性有时能导致集体的非理性——聪明的人类会因自己的聪明而作茧自缚。
1.2 旅行者困境
两个旅行者从一个以出产细瓷花瓶著称的地方旅行回来,他们都买了花瓶。提取行李的时候,发现花瓶被摔坏了,于是他们向航空公司索赔。航空公司知道花瓶的价格大概在八九十元的价位浮动,但是不知道两位旅客买的时候的确切价格是多少。于是,航空公司请两位旅客在100元以内自己写下花瓶的价格。如果两人写的一样,航空公司将认为他们讲真话,就按照他们写的数额赔偿;如果两人写的不一样,航空公司就认定写得低的旅客讲的是真话,并且原则上按这个低的价格赔偿,同时,航空公司对讲真话的旅客奖励2元,对讲假话的旅客罚款2元。
为了获取最大赔偿而言,本来甲乙双方最好的策略,就是都写100元,这样两人都能够获赔100元。可是不,甲很聪明,他想:如果我少写1元变成99元,而乙会写100元,这样我将得到101元。何乐而不为?所以他准备写99元。可是乙更聪明,他算计到甲要算计他写99元,于是他准备写98元。想不到甲还要更聪明一个层次,估计到乙要写98元来坑他,于是他准备写97元……大家知道,下象棋的时候,不是说要多“看”几步吗,“看”得越远,胜算越大。你多看两步,我比你更强多看三步,你多看四步,我比你更老谋深算多看五步。在花瓶索赔的例子中,如果两个人都“彻底理性”,都能看透十几步甚至几十步上百步,那么上面那样“精明比赛”的结果,最后落到每个人都只写一两元的地步。事实上,在彻底理性的假设之下,这个博弈唯一的纳什均衡,是两人都写0。
1.3 智猪博弈
猪圈里有两头猪,一头大猪,一头小猪。猪圈的一边有个踏板,每踩一下踏板,在远离踏板的猪圈的另一边的投食口就会落下少量的食物。如果有一只猪去踩踏板,另一只猪就有机会抢先吃到另一边落下的食物。当小猪踩动踏板时,大猪会在小猪跑到食槽之前刚好吃光所有的食物;若是大猪踩动了踏板,则还有机会在小猪吃完落下的食物之前跑到食槽,争吃到另一半残羹。那么,两只猪各会采取什么策略?答案是:小猪将选择“搭便车”策略,也就是舒舒服服地等在食槽边;而大猪则为一点残羹不知疲倦地奔忙于踏板和食槽之间。原因何在?因为,小猪踩踏板将一无所获,不踩踏板反而能吃上食物。对小猪而言,无论大猪是否踩动踏板,不踩踏板总是好的选择。反观大猪,已明知小猪是不会去踩动踏板的,自己亲自去踩踏板总比不踩强吧,所以只好亲历亲为了。
改变方案一:减量方案。投食仅原来的一半分量。结果是小猪大猪都不去踩踏板了。小猪去踩,大猪将会把食物吃完;大猪去踩,小猪将也会把食物吃完。谁去踩踏板,就意味着为对方贡献食物,所以谁也不会有踩踏板的动力了。
如果目的是想让猪们去多踩踏板,这个游戏规则的设计显然是失败的。
改变方案二:增量方案。投食为原来的一倍分量。结果是小猪、大猪都会去踩踏板。谁想吃,谁就会去踩踏板。反正对方不会一次把食物吃完。小猪和大猪相当于生活在物质相对丰富的“共产主义”社会,所以竞争意识却不会很强。
对于游戏规则的设计者来说,这个规则的成本相当高(每次提供双份的食物);而且因为竞争不强烈,想让猪们去多踩踏板的效果并不好。
改变方案三:减量加移位方案。投食仅原来的一半分量,但同时将投食口移到踏板附近。结果呢,小猪和大猪都在拼命地抢着踩踏板。等待者不得食,而多劳者多得。每次的收获刚好消费完。
对于游戏设计者,这是一个最好的方案。成本不高,但收获最大。许多人并未读过“智猪博弈”的故事,但是却在自觉地使用小猪的策略。股市上等待庄家抬轿的散户;等待产业市场中出现具有赢利能力新产品、继而大举仿制牟取暴利的游资;公司里不创造效益但分享成果的人,等等。比如,公司的激励制度设计,奖励力度太大,又是持股,又是期权,公司职员个个都成了百万富翁,成本高不说,员工的积极性并不一定很高。这相当于“智猪博弈”增量方案所描述的情形。但是如果奖励力度不大,而且见者有份(不劳动的“小猪”也有),一度十分努力的大猪也不会有动力了----就象“智猪博弈”减量方案一所描述的情形。最好的激励机制设计就象改变方案三----减量加移位的办法,奖励并非人人有份,而是直接针对个人(如业务按比例提成),既节约了成本(对公司而言),又消除了“搭便车”现象,能实现有效的激励。
1.4 酒吧博弈问题(barproblem)
酒吧博弈问题是美国人W.B.Arthur1994年在《美国经济评论》发表的题为《归纳论证和有界理性》一问中提出的,然后他又从1999年的《科学》杂志上发表的《复杂性和经济学》一文中阐述了这个博弈。""该博弈是说:有一群人,例如n=100,每个周末,均要决定是去一酒吧活动还是呆在家里。酒吧的容量是有限的,假定是60人。如果某人预测去酒吧的人超过60人,那么他决定去还是不去?……每个参与者或决策者面临的信息只是以前去酒吧的人数,只能根据以前的人数的信息来归纳出策略来。这是一个典型的动态博弈问题……通过计算机的模型实验,阿瑟得出了一个有意思的结果:不同的行动者是根据自己的归纳来行动的,并且,去酒吧的人数没有一个固定的规律,然而,经过一段时间以后,去的平均人数总是趋于60。阿瑟说,预测者自组织到一个均衡系统中去和不去的人群,或形成一个生态稳定系统……这就是酒吧问题。酒吧问题所反映的是这样一个社会现象,正象阿瑟教授说的那样,我们在许多行动中,要猜测别人的行动,然而我们没有更多关于他人的信息,我们只有通过分析过去的历史来预测未来。
二、博弈的基本要素
参与人(Players):指作决策的个体,每个参与人的目标都是通过选择行为来最大化自身的效用。有时候,模型会明确引入“虚拟参与人(pseudo-players)”这个概念,这个角色通常以纯机械般的方式来采取德。比如说“自然”就是一种虚拟参与人,它在博弈的特定时点上以特定的概率随机选择行为。
一个策略式博弈包括:
- 玩家集\(N\):玩家的有限集合
- 每个玩家\(i\)都有策略集\(A_i\),表示他可以选择的策略的集合
- 每个玩家\(i\)都有收益函数\(u_i\):\(A_1 \times A_2 \times \dots A_N \rightarrow R\)表示在一组策略下它的收益
此外,有如下定义:
- 博弈结果:\(a = (a_1,a_2,\dots,a_N)\)是一组策略构成的元组
- 博弈结果空间:\(A = A_1 \times A_2 \times \dots A_N\),则\(a \in A\)
- 对手策略:\(a_{-i} = (a_1,\dots,a_{i-1}, a_{i+1},\dots,a_N)\),则\(a=(a_i,a_{-i})\)
在策略式博弈中,收益的具体数值并不重要,重要的是收益之间的大小关系,称作偏好关系。任何满足全序关系的集合,都可以用来表示收益。我们通常用实数来表示收益。
行动(Action):
信息(Information):在模型化的时候,通常以信息集(information set)的概念来进行,信息集指的是参与人认为博弈可能已到达的结的集合。信息集可以表示出自然的不可观测行为的。
策略(Strategies):一个关于参与人行为程序的完备集合,它告诉参与人在每一种可预见的情况下选择什么行动(即使参与人并不预期那种情况会真的出现)。
支付(Payoffs):采取某种策略后,参与人各自获得的一个利益盈亏的一个估量。
结果(Outcome):指博弈结束之后,建模者从行为、支付及其它变量的取值中所挑选出来的他所感兴趣的要素的集合。
均衡(Equilibria):指参与人最大化各自的支付时所选取的策略。
一个博弈的描述包括:参与人、策略、支付,行动与信息则是它的建筑材料,参与人、行动与结果合起来称之为博弈的规则(Rules Of The Game),建模者的目的在于运用博弈的规则来确定均衡。
三、博弈的分类
博弈可以按照不同的分类方式进行分类,比如按照博弈者出招的顺序,博弈者对其他参与博弈者特征、策略空间和收益是否了解进行分类。
3.1按照博弈者出招的顺序、博弈持续时间和重复次数
博弈可以分为静态博弈(Static Game)和动态博弈(Dynamic Game)。静态博弈指的是参与博弈的各方同时采取策略,这些博弈者的收益取决于博弈者们不同的策略组合。因此静态博弈又称为“同时行动的博弈”(Simultaneous-Move Games)。有时候博弈方采取策略有先后,但是他们并不知道之前其他人做出的策略。比如“囚徒困境”中罪犯1采取策略后,轮到罪犯2采取策略时他并不知道罪犯1所做出的策略。动态博弈(序贯博弈)指的是在博弈中,参与博弈的博弈方所采取策略是有先后顺序的(Sequential-Move),且博弈者能够知道先采取策略者所选择的策略。
3.2根据博弈方的收益
博弈可以分为零和博弈(Zero-Sum Game)与非零和博弈(Non-Zero-Sum Game),常和博弈(Constant-Sum Game)与变和博弈(Variable-Sum Game)
3.3博弈者对其他参与博弈者所了解的信息的完全程度
博弈可以分为完全信息博弈(Complete Information Game)与不完全信息博弈(Incomplete Information Game),以及完美信息博弈(Perfect Information Game)与不完美信息博弈(Imperfect Information Game),确定的博弈(Certainty Game)与不确定的博弈(Uncertain Game),对称信息博弈(Symmetric Game)与非对称信息博弈(Asymmetric Game)等等。
其中,完全信息是指博弈中每一个博弈者对其他博弈者的特征、策略空间和收益函数都了解,也就是博弈者的收益集(Pay offs)是所有博弈者都知道的。完美信息是指博弈者完全知道在他采取策略时其他博弈者的所有策略信息。完美信息是针对记忆而言,也就是他知道博弈已经发生过程的所有信息。又或者说,如果博弈者在采取策略时观察到他所处的信息节点是唯一的,即他知道以前发生的所有事情,如果所处的信息节点不唯一,说明他对之前的信息没有完美的记忆(不知道博弈过程是怎么过来的)。因此,完全信息不一定是完美的,不完全信息一定不是完美的。
如果某个博弈者对其他博弈者的特征、策略空间和收益函数了解不够全面,或者说不是对所有博弈者的上述信息了解全面。这种博弈叫做不完全信息博弈,博弈者的目标是最大化自己收益的期望。在不完全信息博弈中,首先行动的是自然(Nature),自然决定博弈者以多大的可能性采取某种策略,这个可能性只有本人知道。确定的博弈指的是不存在由自然做出这种行动的博弈,要不然就是不确定的博弈。
3.4博弈者之间是否有合作关系
博弈可以分为合作博弈(Cooperative Game)和非合作博弈(Non-Cooperative Game)。
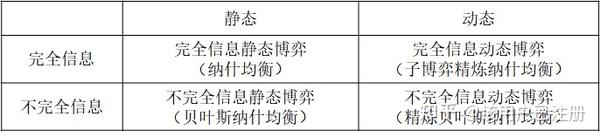
合作博弈指的是博弈者之间有着一定的协议,他们需要在协议允许的范围内博弈。比如两个企业之前通过一定的谈判达成协议,对各自的产量或价格进行操作,以达到共同垄断市场的行为。反之如果博弈者不能通过谈判达成一个有约束力的协议来限制博弈者的策略,那么就是非合作博弈。非合作博弈可以分为:完全信息静态博弈、完全信息动态博弈、不完全信息静态博弈、不完全信息动态博弈,这是博弈论的主流框架。与之对应的有四种均衡:纳什均衡(Nash Equilibrium)、子博弈精炼纳什均衡(Subgame Perfect Nash Equilibrium)、贝叶斯纳什均衡(Bayesian Nash Equilibrium)、精炼贝叶斯纳什均衡(Perfect Bayesian Nash Equilibrium)。它们的关系如下表
四、博弈的策略式
集合\(G = \{N, \{ A_i \}_{i=1}^N, \{ u_i \}_{i=1}^N \}\)称作策略式博弈G,其中\(N,A_i,u_i\)就是前面定义的那样。
例1:囚徒困境策略式
- 玩家集:\(N = \{1,2\}\),表示1、2两个囚徒
- 策略集:坦白,沉默\(A_1 = A_2 = \{坦白,沉默\}\),为了书写简便,用\(c\)表示坦白,用\(d\)表示沉默
- 收益函数:
-
\[u_{1}(c, c)=-6, u_{1}(c, d)=0, u_{1}(d, d)=-1, u_{1}(d, c)=-12 \]
-
\[u_{2}(c, c)=-6, u_{2}(c, d)=-12, u_{2}(d, d)=-1, u_{2}(d, c)=0 \]
- 用收益矩阵表示如下:
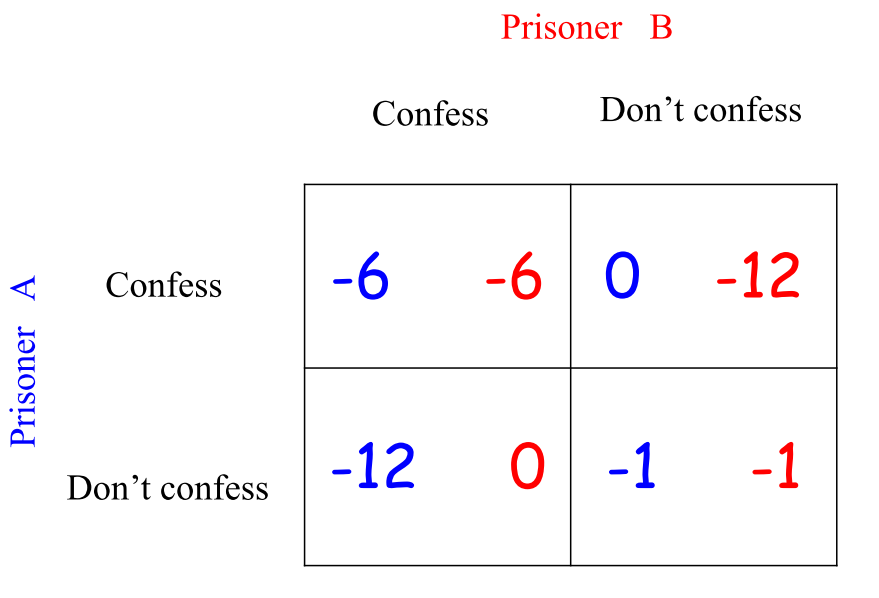
例2:古诺竞争博弈
设两个厂商\(\{1, 2\}\)生产和销售同一种商品,厂商\(i\)生产的数量记为\(q_i\)。 每件商品生产成本都是\(c\),售价是:\(max(0,a-b(q_1+q_2))\)。
其中,收益\(u_i(q_1,q_2) = (max(0,a-b(q_1+q_2))-c)q_i\)。(售价-成本)x生产数量
参考文献
- 博弈论(Game Theory)入门——基础知识
- 博弈论笔记(一):策略式博弈及其纳什均衡
- 博弈的分类及组成要素