论文阅读 | Layer-wised Model Aggregation for Personalized Federated Learning

laolao's Blogs / 2023-08-09 / 原文

面向个性化联合学习的分层模型聚合

在本文中，我们提出了一种新的pFedLA训练框架，该框架能够区分不同客户端的每一层的重要性，从而能够优化具有异构数据的客户端的个性化模型聚合。具体来说，我们在服务器端为每个客户端使用一个专用的超网络，它被训练来识别层粒度上的相互贡献因素。同时，引入参数化机制更新分层聚合权值，逐步利用用户间的相似度，实现精确的模型个性化。在不同的模型和学习任务中进行了大量的实验，我们表明，所提出的方法比最先进的pFL方法取得了明显更高的性能。

1 介绍

联邦学习(FL)已经成为一个突出的协作机器学习框架，可以在不共享私有数据的情况下利用用户间的相似性[33,43,52]。当用户的数据集是非iid(独立且同分布)，即用户间距离较大时[23,53]，所有客户共享一个全局模型可能会导致收敛速度慢或推理性能差，因为模型可能会显著偏离其本地数据[14,56]。
为了处理这种统计多样性，提出了个性化联邦学习(pFL)机制，允许每个客户端训练一个定制的模型，以适应自己的数据分布[9,12,15,22]。文献在实现pFL方面的现状包括基于数据的方法，即平滑客户数据集之间的统计异质性[8,16]，单模型方法，如正则化[22,41]，元学习[9]，参数解耦[5,24,26]，以及多模型方法，即为每个客户训练个性化模型[15，54]，通过客户模型的加权组合，可以为每个客户生成个性化的模型。现有的pFL方法在整个模型参数或不同客户的损耗值之间采用距离度量，这不足以利用它们的异构性，因为总体距离度量不能总是反映每个局部模型的重要性，并可能导致不准确的权重组合或非iid分布式数据集的贡献不平衡，从而阻止进一步大规模的客户个性化。主要原因是神经网络的不同层可以有不同的用途，例如，浅层更侧重于局部特征提取，而深层则用于提取全局特征[6,20,21,47,49]。度量模型的距离会忽略这些层次上的差异，导致不准确的个性化，从而影响pFL的训练效率。

图1 一个简单的例子:分层聚合法 vs. 模型聚合法。
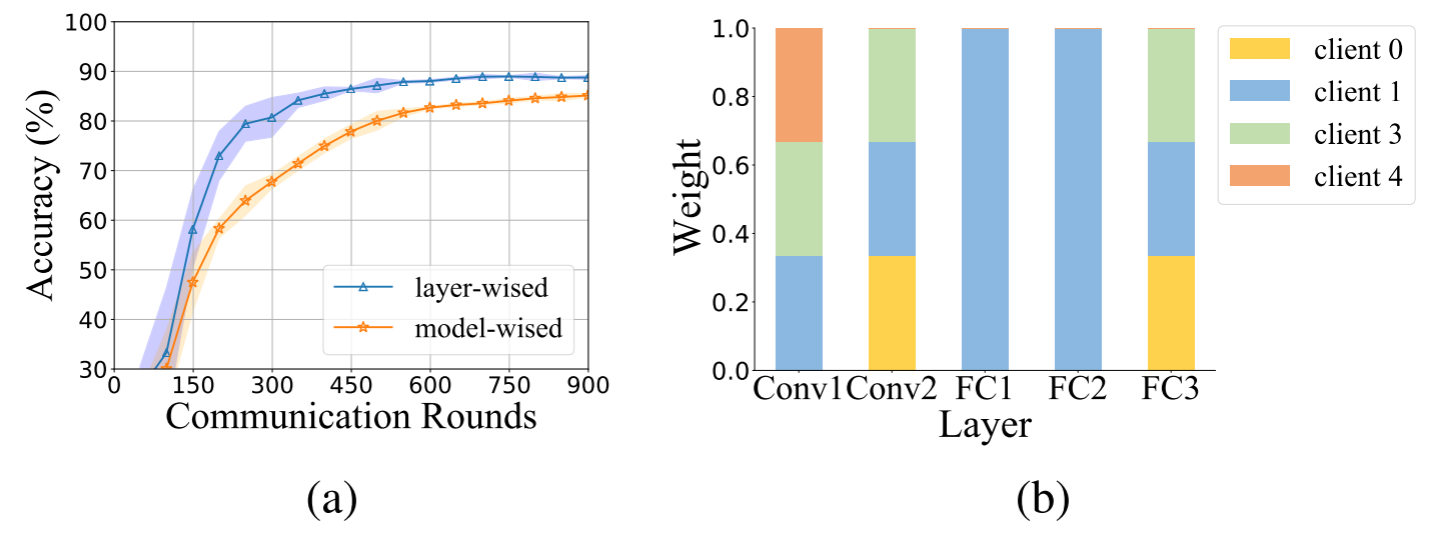
(a) 客户端1的模型性能。两种方法都采用了基于相似度的个性化聚合。即，分层聚合法：通过计算层之间的相似度来进行个性化聚合；模型聚合法：通过计算模型之间的相似度来进行个性化聚合。 (b) 客户端1在最后一轮通信中每一层的权重。

观察分层个性化聚合。 在这个例子中，我们考虑了六个客户端协同学习他们的个性化模型，用于一个九类分类任务。平均模型准确率是通过分层聚合法和模型聚合法得到的，它们分别利用了层间和模型间的相似度。图1显示了对于某个客户端，分层聚合法相比模型聚合法可以获得更高的模型准确率。我们还绘制了客户端最后一轮通信后每一层的权重，并显示了对不同的层应用不同的权重，例如，客户端1的第一和第二全连接层（即FC1, FC2）有较大的权重，而第二卷积层，即Conv1层有较小的权重，可以显著提高个性化模型的准确率。这个例子展示了分层聚合法相比传统的基于模型的个性化联邦学习方法，能够获得更高的性能的潜力，因为层级的相似度可以更准确地反映客户端之间的相关性。通过利用这种分层相似度和识别层级的跨用户贡献，有望为所有客户端生成高效和有效的个性化模型。

受此启发，我们提出了一种新颖的联邦训练框架，即pFedLA，能够以分层的方式自适应地促进客户端之间的底层协作。具体来说，在服务器端，为每个客户端引入了一个专用的超网络，用于在个性化联邦学习训练过程中学习跨客户端层的权重，这被证明可以有效地提高在非独立同分布数据集上的个性化程度。我们实验证明了所提出的pFedLA可以在广泛使用的模型和数据集上，即EMNIST, FashionMNIST, CIFAR10和CIFAR100，比最先进的基线方法获得更高的性能。本文的贡献总结如下：

这篇论文是第一个明确揭示了在异构FL客户端中，分层智能聚集与模型智能方法的好处;
提出了一种分层的个性化联邦学习(pFedLA)训练框架，可以有效地利用非iid数据的客户之间的用户间相似性，并产生准确的个性化模型;
在4个典型的图像分类任务上进行了广泛的实验，证明了pFedLA比最先进的方法有更好的性能。

2 相关工作

2.1 个性化联合学习

实现个性化联邦学习可以分为基于数据和基于模型的两大类。基于数据的方法侧重于减少客户端数据集之间的统计异质性，以提高模型的收敛性，而基于模型的方法强调为不同的客户端生成定制化的模型结构或参数。

基于数据的个性化联邦学习：典型方法是将一小部分全局数据共享给每个客户端。

Jeong等人关注了通过生成额外的数据来增加其本地数据，从而产生一个独立同分布数据集的数据增强方法。然而，这些方法通常需要联邦学习服务器知道客户端本地数据分布的统计信息（例如，类别大小，均值和标准差），这可能会违反隐私政策。
另一类工作考虑设计客户端选择机制来接近均匀的数据分布。

基于模型的个性化联邦学习： 分为两种类型单模型，多模型方法。

单模型方法是从传统的联邦学习算法（如FedAvg）扩展而来的，它们将本地模型和全局模型的优化结合起来，包括五种不同的方法：本地微调，正则化，模型混，元学习和参数分解。
考虑到本地数据的多样性和内在关系，多模型方法即为异构客户端训练多个全局模型，更为合适。一些研究者提出了在服务器端训练多个全局模型的方法，其中将相似的客户端聚类成几个组，并为每个组训练不同的模型。另一种策略是协同训练每个个体客户端的个性化模型，例如FedAMP, FedFomo, MOCHA, KT-pFL等。

我目前的研究属于多模型方法的第一类

这些文献将每个客户端的模型视为一个整体实体，并且还没有考虑到层级的效用对于个性化聚合的影响。用于描述模型之间相似度的距离度量是不准确的，并且可能导致次优的性能，这促使我们探索一种细粒度的聚合策略来适应广泛范围的非独立同分布客户端。

2.2. 超网络

超网络（Hypernetworks）是一种用于生成其他神经网络的参数的方法，它通过将目标任务的嵌入映射到相应的模型参数。超网络已经广泛应用于各种机器学习应用中，例如语言建模，计算机视觉，3D场景表示，超参数优化，神经架构搜索（NAS），持续学习和元学习。Shamsian等人是第一个将超网络应用于联邦学习的工作，它可以为每个客户端生成有效的个性化模型参数。我们展示了超网络能够评估每个模型层的重要性，并且可以提升非独立同分布场景下的个性化聚合。

3 模型

3.1. 问题描述

考虑到N个客户端具有非独立同分布的数据集，令$\mathcal{D}_{i}=\{(x_{j}^{(i)},y_{j}^{(i)})\}_{i=1}^{m_{i}}(1 \leq i \leq N)$表示第$i$个客户端上的数据集，其中$x_j$是第j个输入数据样本，$y_j$是相应的标签。第$i$个客户端上的数据集的大小用$m_i$表示。所有客户端数据集的大小为$\begin{aligned}M&=\sum_{i=1}^Nm_i\end{aligned}$。令$θ_i$表示客户端i的模型参数，个性化联邦学习的目标可以表述为：

\[\Theta^*=\arg\min_{\Theta}\sum_{i=1}^N\frac{m_i}{M}\mathcal{L}_i(\theta_i),\quad(1) \\ \mathcal{L}_i(\theta_i)=\frac{1}{m_i}\sum_{j=1}^{m_i}\mathcal{L}_{CE}(\theta_i;x_j^{(i)},y_j^{(i)})\quad(2) \]

其中$\Theta=\{\theta_{i},\ldots,\theta_{N}\}$是所有客户端的个性化参数的集合。$L_i$是与数据集$D_i$相关的第i个客户端的损失函数。数据样本的预测值和真实标签之间的差异由$L_{CE}$测量，它是交叉熵损失函数。

3.2. pFedLA算法

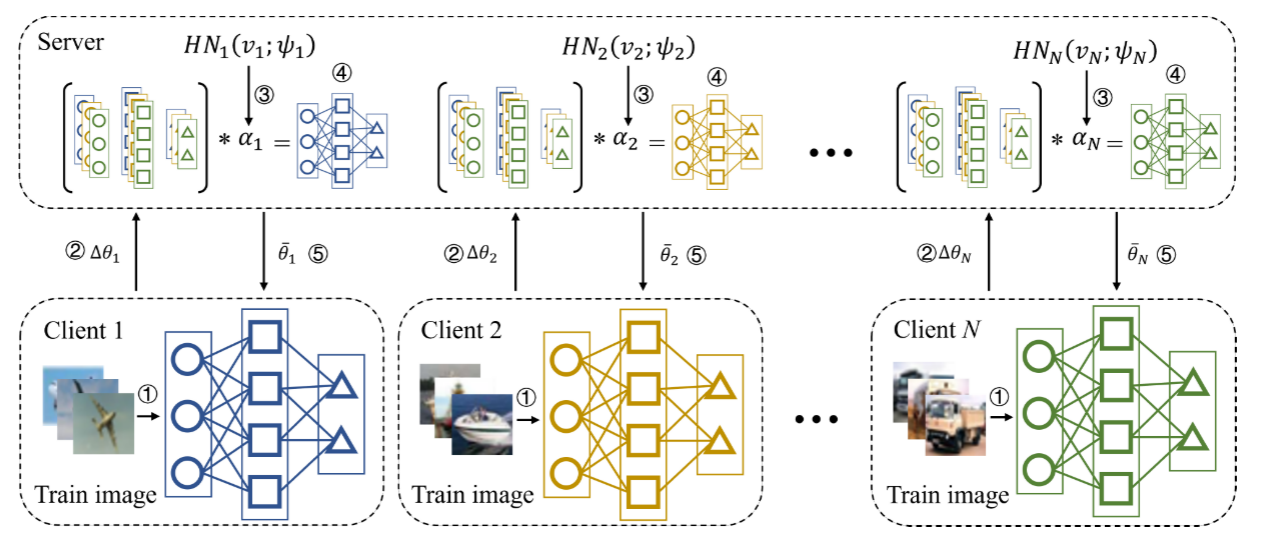
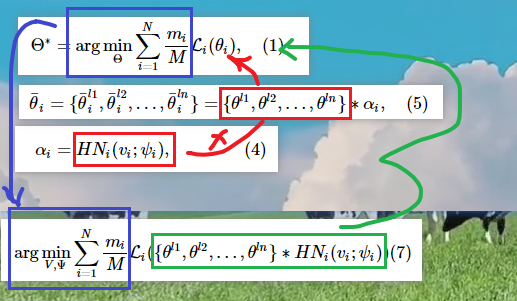
图2. pFedLA的框架。工作流程包含5个步骤：①在私有数据上进行本地训练；②每个客户端将参数更新 $∆θ_i$发送到服务器；③服务器根据$∆θ_i$通过超网络$HN_i(v_i; ψ_i)$更新聚合权重矩阵$α_i$；④服务器进行加权聚合并输出对应客户端的个性化模型$\hat{θ}_i$；⑤每个客户端下载个性化模型$\hat{θ}_i$。

pFedLA可以评估不同客户端的每一层的重要性，从而实现分层的个性化模型聚合。服务器端为每个客户端应用一个专用的超网络，来生成客户端每层模型的聚合权重。从图2可以看出，pFedLA在服务器端维护每个客户端的个性化模型。具有相似数据分布的客户端应该具有高的聚合权重，以加强彼此之间的相互贡献。pFedLA在服务器端应用了一组聚合权重矩阵$α_i$，以逐步利用层级上的跨用户相似度，它定义为:

\[\alpha_i=\begin{bmatrix}\alpha_i^{l1},\alpha_i^{l2},\ldots,\alpha_i^{ln}\end{bmatrix}=\begin{bmatrix}\alpha_i^{l1,1}&\alpha_i^{l2,1}&\cdots&\alpha_i^{ln,1}\\\alpha_i^{l1,2}&\alpha_i^{l2,2}&\cdots&\alpha_i^{ln,2}\\\vdots&\vdots&\ddots&\vdots\\\alpha_i^{l1,N}&\alpha_i^{l2,N}&\cdots&\alpha_i^{ln,N}\end{bmatrix}(3) \]

$α^{ln}_i$：客户端i中，第n层的聚合权重向量
$α^{ln,N}_i$：第n层中客户端N的聚合权重。
对于所有n层，有$\begin{aligned}\sum_{j=1}^N\alpha_i^{ln,j}&=1\end{aligned}$。

pFedLA是考虑到神经层的不同效用为每个层分配一个唯一的权重，以实现细粒度的个性化聚合。此外，与传统的方法不同(使用整个模型参数之间的距离度量来数学地计算权重)，pFedLA通过一组专用的超网络在训练阶段对权重进行参数化。层级的权重由超网络决定，它们与个性化模型交替更新。这样可以得到有效的权重，因为它们的更新方向与目标函数的优化方向一致。在下面，将详细介绍pFedLA的聚合权重矩阵α的更新过程。

每个超网络由若干个全连接层组成，其输入是一个嵌入向量，该向量会随着模型参数自动更新，而输出是权重矩阵α。定义客户端i上的超网络为

\[\alpha_i=HN_i(v_i;\psi_i),\quad\quad\quad\quad(4) \]

$v_i$是嵌入向量
$ψ_i$是客户端i的超网络的参数（即图3）。

图3. pFedLA中使用的一种超网络框架的示意图。超网络$HN_i$以嵌入向量$v_i$为输入，输出聚合权重矩阵$α_i$。在用中间参数$\{\theta^{l\operatorname{1}},\ldots,\theta^{l\operatorname{n}}\}$和聚合权重矩阵$α_i$进行加权组合后，客户端i可以在私有数据上进行本地训练。注意，$v_i$和$ψ_i$都会在训练过程中更新。

$\{\theta^{l1},\theta^{l2},\ldots,\theta^{ln}\}$是所有客户端在本地训练后的中间参数，$\begin{aligned}\theta^{ln}=\{\theta_1^{ln},\theta_2^{ln},\ldots,\theta_N^{ln}\}\end{aligned}$是所有客户端的第n层的参数集合，其中$\theta_N^{ln}$是客户端N的第n层的参数。在pFedLA中，客户端i的模型参数是根据$α_i$进行加权聚合得到的：

\[\bar{\theta}_i=\{\bar{\theta}_i^{l1},\bar{\theta}_i^{l2},\ldots,\bar{\theta}_i^{ln}\}=\{\theta^{l1},\theta^{l2},\ldots,\theta^{ln}\}*\alpha_i,\quad(5) \]

因此，pFedLA的目标函数可以由式1推导到

\[\begin{aligned}\arg\min_{V,\Psi}\sum_{i=1}^N\frac{m_i}{M}\mathcal{L}_i(\{\theta^{l1},\theta^{l2},\ldots,\theta^{ln}\}*HN_i(v_i;\psi_i))(7)\end{aligned} \]

其中$V~=~\{v_1,\ldots,v_N\},~\Psi~=~\{\psi_1,\ldots,\psi_N\}.$因此，pFedLA将客户端参数$θ_i$的优化问题转化为超网络的嵌入向量$v_i$和参数$ψ_i$。接下来，介绍$V$和$Ψ$的更新规则。

更新$v_i$和$ψ_i$。 根据链式法则，可以从公式7得到$v_i$和$ψ_i$的梯度：

\[\begin{aligned} \begin{aligned} \nabla_{v_i}\mathcal{L}_i=(\nabla_{v_i}\bar{\theta}_i)^T\nabla_{\bar{\theta}_i}\mathcal{L}_i \end{aligned} \begin{aligned}=[\{\theta^{l1}\theta^{l2},\ldots,\theta^{ln}\}*\nabla_{v_i}HN_i(v_i;\psi_i)]^T\nabla_{\bar{\theta}_i}\mathcal{L}_i,\end{aligned}.\text{(8)}\\ \begin{aligned}\nabla_{\psi_i}\mathcal{L}_i=(\nabla_{\psi_i}\bar{\theta}_i)^T\nabla_{\bar{\theta}_i}\mathcal{L}_i\end{aligned} =[\{\theta^{l1},\theta^{l2},\ldots,\theta^{ln}\}*\nabla_{\psi_i}HN_i(v_i;\psi_i)]^T\nabla_{\bar{\theta}_i}\mathcal{L}_i.\text{(9)} \end{aligned} \]

$\nabla_{\bar{\theta}_i}\mathcal{L}_i$可以从每个通信轮的客户端i的本地训练中获得，而$\nabla_{v_{i}/\psi_{i}}HN_{i}(v_{i};\psi_{i})$是$α_i$在$v_{i}/\psi_{i}$方向上的梯度。pFedLA使用了一种更一般的方法来更新$v_i$和$ψ_i$：

\[\begin{aligned} \Delta v_{i}=(\nabla_{v_{i}}\bar{\theta}_{i})^{T}\Delta\theta_{i} \\ &\left(10\right) \\ =[\{\theta^{l1},\theta^{l2},\ldots,\theta^{ln}\}*\nabla_{v_{i}}HN_{i}(v_{i};\psi_{i})]^{T}\Delta\theta_{i}, \\ \Delta\psi_{i}=(\nabla_{\psi_{i}}\bar{\theta}_{i})^{T}\Delta\theta_{i} \\ &\begin{pmatrix}11\end{pmatrix} \\ =[\{\theta^{l1},\theta^{l2},\ldots,\theta^{ln}\}*\nabla_{\psi_{i}}HN_{i}(v_{i};\psi_{i})]^{T}\Delta\theta_{i}. \end{aligned} \]