CF1439B Graph Subset Problem

​ 给定一个 \(n\) 个点和 \(m\) 条边的无向图，和一个整数 \(k\) 。找出图中大小为 \(k\) 的团（称一个 \(k\) 个点的集合为团，当且仅当点集大小为 \(k\)，并且该子集的每两个顶点之间存在一条边） 或一个非空的顶点子集，使该子集的每个顶点在该子集中至少有 \(k\) 个邻居。输出方案，若无解输出 \(-1\) ，\(T\) 组数据。

​ \(T\le10^5 \; \; n,m,k\le10^5 \;\;\sum{n}\le2\times 10^5\)

容易发现度数小于 \(k-1\) 的点没有贡献，所以我们考虑先删去图中所有度数小于 \(k-1\) 的点，方法类似于拓扑排序。对于剩下的点，若它的度数为 \(k-1\) ，则可能形成一个大小为 \(k\) 的团，那我们假设它确实在团中，那我们暴力枚举其出边，验证是否在团中，即验证是否所有点两两都有连边。这的复杂度为 $O(k^2B) $ ，其中 \(B\) 是判断两个点是否有连边的复杂度，可以将所有点出边排序然后二分查找，也可以哈希一下（但 CF 哈希可能会被 hack )。如果它在团中直接输出即可，否则把这个点类似地删去。不断重复此过程，最终若还有点剩余，说明这些点的度数至少为 \(k\) ，输出即可，否则无解。

对于时间复杂度，度数大于等于 \(k-1\) 的点的个数是 \(\frac{m}{k}\) ，枚举团时满足 \(k\le\sqrt{m}\) ，所以总时间复杂度为 \(O(m\sqrt{m})\) 。

CF191D Metro Scheme

​ 给定一个 \(n\) 个点 \(m\) 条边的仙人掌（满足每个点至多属于一个简单环），要求用简单路径和简单环恰好覆盖所有边，求数目的最小值和最大值。

​ \(n\le10^5 \;\,m\le3\times 10^5\)

容易发现用简单路径覆盖一定比简单环不劣（前提是整个图不是一个简单环）。因为每个环至少有一条出边，把环断开然后连向出边必然不劣。然后我们就可以考虑 tarjan 边双缩点找出所有的环，剩下的就是森林。对于这些点，其答案为 \(\sum^{n}_{i=1} {d_i \bmod 2}\)，其中 \(d_i\) 为点 \(i\) 的度数。然后再考虑那些环上的点，如果一个环的出边大于等于 \(2\) ，那么它肯定可以从一条边进入，再从一条边出去，恰好将环覆盖，不需要新的边。否则我们还需要单独用一条边才能将其覆盖。

注意边双大小为 \(1\) 以及 \(m=0\) 的情况，时间复杂度 \(O(N+M)\) 。

[BalkanOI2011]最小乘积生成树

​ 给定一个 \(n\) 个点 \(m\) 条边的无向图，每条边有两个权值 \(a,b\) 。求该图的一个生成树 \(T\) ，使得 \((\sum_{e \in T} {a_e}) \times (\sum_{e \in T} {b_e})\) 最小，输出 \(\sum_{e \in T} {a_e}\) 和 \(\sum_{e \in T} {b_e}\) ，若有多解则输出 \(\sum_{e \in T} {a_e}\) 最小的那个。

​ \(1\le n\le 200 \;\; 1\le m \le 10000 \;\; 0\le a_i,b_i \le 255\)

**前置知识：向量的叉乘运算。令 \(\alpha \;=\;<\vec{a},\vec{b}>\) ，则\(|\vec{a} \times \vec{b}| =|\vec{a}| \cdot |\vec{b}|\cdot sin\alpha\)，结果是一个向量，若 \(\vec{a}\) 到 \(\vec{b}\) 需要逆时针旋转，模结果为负，否则为正。对于其坐标运算，设 \(\vec{a}=(x_1,y_1),\vec{b}=(x_2,y_2)\) ，则 \(|\vec{a} \times \vec{b}|= x_1 \cdot y_2-x_2 \cdot y_1\) **

我们令 \(\sum_{e \in T} {a_e}\) 为 \(x\) ，\(\sum_{e \in T} {b_e}\) 为 \(y\)，那么我们就是要在二维平面内找一个 \(x\times y\) 最小的点。容易发现这样的点在一个下凸壳上，我们先分别求出 \(x\) 和 \(y\) 的最小值，只需要分别以 \(a_i\) 和 \(b_i\) 为边权做一遍最小生成树即可。此时对应的两个点分别为 \(A\) 和 \(B\) ，然后我们要找到一个在 \(AB\) 的下方且离 \(AB\) 最远的点 \(C\) ，我们发现这等价于 \(S_{△ABC}\) 最大，我们考虑 \(S_{△ABC} = -\frac{1}{2} \vec{AB} \times \vec{AC}\) 。

$\vec{AB} \times \vec{AC} = (x_B-x_A)(y_C-y_A) -(x_C-x_A)(y_B-y_A) $

​ \(\,\,=(x_B-x_A)y_C+(y_A-y_B)x_C-(x_B-x_A)y_A+(y_B-y_A)x_A\)

容易发现后两项与 \(C\) 无关，所以我们需要最小化前两项。所以我们又可以将边权设为 \((y_A-y_B)a+(x_B-x_A)b\) ，跑一遍最小生成树就能得到对应的点 \(C\) 坐标。然后我们又可以递归求解 \(AC\) 和 \(BC\) ，当求出来的点不在 \(AB\) 下方时结束递归，我们只需要算一下 \(\vec{AB} \times \vec{AC}\) ，若结果为负，说明 \(C\) 在 \(AB\) 下方。这样我们就可以得到所有的决策点，每次在求最小生成树的时候更新答案即可。

因为我们要做凸包上的点数次最小生成树，所以时间复杂度为 \(O(Bmlogm)\) ，其中 \(B\) 为凸包上的点数。

CF1513F Swapping Problem

​ 给定 \(n\) 和两个长度为 \(n\) 的序列 \(a,b\) ，可以交换一次 \(b\) 中的两个位置的值。最小化 \(\sum_{i=1}^n|a_i-b_i|\) 。

​ \(n\le 2\times 10^5\)

我们考虑将 \(a,b\) 序列形象化表示，将 \(a_i,b_i\) 看作一段区间，那么 \(|a_i-b_i|\) 就是区间的长度，我们可以交换两个区间的 \(b\) 端使得原长度减去新长度的值最大。

我们可以先对两端区间的位置进行讨论，看看什么时候交换可以使答案变小。

• 当两个区间没有交点

容易发现无论怎么交换长度都是会变大

• 当两个区间相包含

不妨设大的区间 \(a_i<b_i\) ，若小的区间 \(a_j<b_j\) ，容易发现答案不会改变。相反当 \(a_j>b_j\) 时，答案会减少。

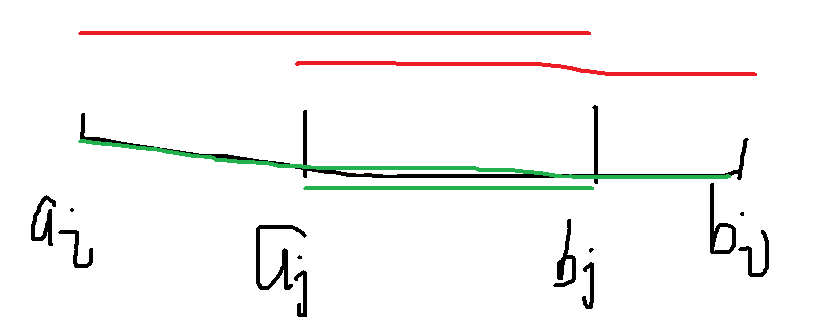
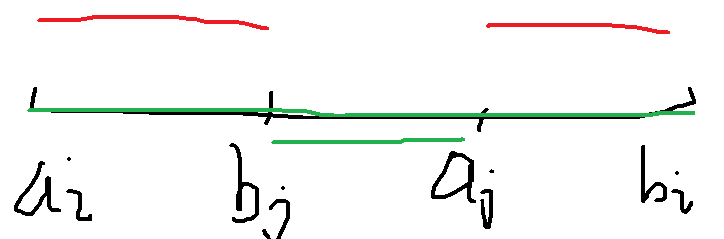
• 当两个区间相交

不妨设左边的区间 \(a_i<b_i\) ，若另一个区间 \(a_j<b_j\) ，容易发现答案不会改变。相反当 \(a_j>b_j\) ，答案会减少。

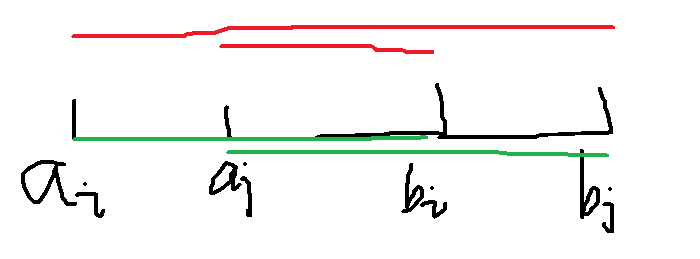
综上，我们可以得到：若交换 \(b\) 可以产生贡献，那么 \((a_i-b_i)(a_j-b_j)<0\) ，且减少的答案为两个区间的交集的长度乘 \(2\) 。

至此我们对所有区间按照 \(a_i\) 是否小于 \(b_i\) 分类，然后全修改为 \(a_i<b_i\) 再按 \(b_i\) 从大到小排序。对于每个类型我们维护已经查询过的最小的 \(a\) 值，而对于每个 \(i\) ，我们查询与它类别不同的区间中最小的 \(a\) 值是多少，并与自己的 \(a\) 值取 \(min\) 再与自己的 \(b\) 值做差就得到了长度最长的交区间，再不断取 \(max\) ，最终用原来的总长度减去两倍的它即可。时间复杂度为 \(O(n\log n)\) 。

CF819E Mister B and Flight to the Moon

​ 给定 \(n\) ，问能否用总共不超过 \(n^2\) 个三元环和四元环覆盖 \(n\) 个点的完全图并使得每条边被恰好覆盖两次。若不能输出 -1 ，否则输出方案。

​ \(3\le n\le 300\)

考虑归纳构造法，假设我们已经知道 \(n-2\) 个点的方案。我们在其中加入两个点 \(n-1\) 和 \(n\) ，容易发现多出了以下边：

• \(\forall 1\le i\le n-2\) ，多出了一条 \(i\) 到 \(n-1\) 的边。

• \(\forall 1\le i\le n-2\) ，多出了一条 \(i\) 到 \(n\) 的边。

• 还多了一条 \(n-1\) 到 \(n\) 的边。

我们考虑如何覆盖上这些边两次。

• 当 \(n\) 为奇数时

我们对于 \(\forall 2\le i\le n-2,i=i+2\) ，我们用两个 \(i,n-1,i+1,n\) 的四元环。最后再用两个 \(1,n-1,n\) 的三元环即可。

• 当 \(n\) 为偶数时

我们对于 \(\forall 3\le i\le n-2,i=i+2\) ，我们用两个 \(i,n-1,i+1,n\) 的四元环。最后再用四元环 \(1,n-1,2,n\) ，三元环 \(1,n-1,n\) 和三元环 \(2,n-1,n\) 即可。

时间复杂度为 \(O(n^2)\) 。

CF1572B Xor of 3

​ 给定一个长度为 \(n\) 的 \(01\) 序列 \(a\) ，一次操作可以选择连续的三个数并把它们都变成原来三个数的异或和。问能否在 \(n\) 次操作内全变成 \(0\) 。

​ \(n\le 2\times 10^5\)

容易发现，每次操作后所有数异或和是不会改变的。我们设 \(s_x=\bigoplus_{i=1}^{x}a_i\) ，那么有解的一个条件是 \(s_n=0\) 。当我们对位置 \(i,i+1,i+2\) 进行操作后，容易发现 \(s_1,s_2,\cdots,s_{i-1},s_{i+2},\cdots,s_n\) 都不会改变，也就是只有 \(s_i,s_{i+1}\) 会改变，我们考虑如何改变。不妨设这三个数都变成了 \(x\) ，那么 \(s_{i+1}=s_{i-1},s_{i+2}=s_i\) （异或了两次所以不变）。

所以我们可以把操作全转化到 \(s\) 上，即给定序列 \(s_0,s_1,\cdots s_n\) ，每次可以选择一个位置 \(i\in[1,n-2]\) ，使得 \(s_{i+1}=s_{i-1},s_{i}=s_{i+2}\) ，要求最终全变成 \(0\) 。

容易发现每次修改都是在奇偶的相邻位置上，偶数位最后肯定能变成 \(0\) 因为 \(s_0=0\) ，所以我们考虑奇数位。我们需要在奇数位上找到一个 \(0\) 即可，也就是说，如果奇数位没有 \(0\) ，那么就无解。然后将奇数位全修改为 \(0\) ，最后将偶数位全修改成 \(0\) 即可。时间复杂度为 \(O(n)\) 。

CF444E DZY Loves Planting

​ 给定一棵 \(n\) 个点的带边权树和长度为 \(n\) 序列 \(a\) ，定义 \(g(x,y)\) 表示 \(x\) 到 \(y\) 的路径上权值的最大值。对于一个长度为 \(n\) 的序列 \(p\) ，我们定义 \(f(p)=\min_{i=1}^{n}g(i,p_i)\) 。若序列 \(p\) 合法，则序列 \(p\) 中元素 \(x\) 出现的次数不超过 \(a_x\) 次，求所有合法序列 \(p\) 中 \(f(p)\) 的最大值。

​ 原题： \(n\le 3000\;\;1\le a_i\le n\) 事实上可以：\(n\le 5\times 10^5\)

原题可以通过二分答案加网络流判定的方法通过。事实上这道题有更优秀的做法。

容易发现题目就是给每个点都分配另外一个点，并且每个点的出现次数都不超过 \(a_x\) 次。我们考虑将边权从小到大排序并进行枚举，然后判断这条边能否成为答案。考虑如何判断，对于一条边连接的两个联通块，我们合并成一个大联通块之后，若大联通块里的点无法与剩下的点配对，那么这条边的权值就是答案了，换句话说，假设大联通块的大小为 \(size\) ，\(\sum_{i=1}^{n}a_i=sum\) ，大联通块里的点的 \(a\) 之和为 \(p\) ，那么当 \(siz>sum-p\) ，这条边就是答案，直接退出即可。\(sum-p\) 表示可以选择联通块外的点的数量，由于边权是从小到大排序枚举，那么联通块里的点要到达外面的点，一定会经过比现在枚举的边权更大的边，并且若 \(siz\le sum-p\) ，那么联通块里的点都一定能分配到一个联通块外的点，那么 \(f(p)\) 一定会大于这条边的边权，否则一定会剩下联通块里的点不能和外面的点匹配，此时只能联通块和联通块里的点进行匹配，那么 \(g\) 肯定就 \(\le\) 当前的边权了，此时 \(f(p)\) 最大就只能是当前的边权了。容易发现这个过程直接用并查集维护即可。时间复杂度为 \(O(n\log n)\) 。

CF1239E Turtle

​ 有一个 \(2\times n\) 的网格，从左上角走到右下角，只能往下或往右，每个格上都有权值。现给定 \(2n\) 个数 \(x\) ，将它们分配到每个格子上，使得所有方案中路径经过的格子上的数字之和的最大值最小。输出方案。

​ \(n\le 25\;\;0<x\le 5\times 10^4\)

容易发现路径一定是先从 \((1,1)\) 走到 \((1,pos)\) ，再走到 \((2,pos)\) ，最终走到 \((2,n)\) ，其中 \(1\le pos\le n\) 。我们可以先找一些性质。

• 第一行的数一定单调不降，第二行的数一定单调不升。

假设第一行存在 \(i<j\) ，\(a_i>a_j\) ，那么当 \(i\le pos<j\) 时，交换 \(a_i,a_j\) 一定更优，因为此时 \(i\) 对权值和的贡献从 \(a_i\) 变为了 \(a_j\) ，答案一定更小。同理可以得出第二行一定要单调不升。

• 最小的数一定填在 \((1,1)\) ，次小的数一定填在 \((2,n)\) 。

由于第一行单调不降，那么 \((1,1)\) 为第一行最小。由于第二行单调不升，那么 \((2,n)\) 为第二行最小。不妨设最小的在 \((1,1)\) ，我们考虑次小的应该放在 \((1,2)\) 还是 \((2,n)\) 。容易发现，当 \(pos=1\) 时，次小的放在 \((2,n)\) 更优，因为放在 \((1,2)\) 起不到贡献；而当 \(pos>1\) 时，无论放哪都会起贡献。所以我们直接让它放在 \((2,n)\) 即可。

• 数字和最大的时候， \(pos\) 一定为 \(1\) 或 \(n\) 。

假设数字和最大的时候，\(1<pos<n\) 。那么 \(pos-1\) 的位置向下走更小，我们可以得到 \((1,pos)\) 的值大于 \((2,pos-1)\) 的值。同理 \(pos+1\) 的位置向下走更小，我们可以得到 \((1,pos+1)\) 的值小于 \((2,pos)\) 的值。写在一起就是，\((1,pos)>(2,pos-1)>(2,pos)>(1,pos+1)\) ，\((1,pos) >(1,pos+1)\) 与第一行单调不降矛盾，所以数字和最大的时候 \(pos\) 只能为 \(1\) 或 \(n\) 。

容易发现，当 \(pos=1\) ，就是 \((1,1)\) 加上 \((2,n)\) 再加上 \((2,1)\) 到 \((2,n-1)\) 的数字和。当 \(pos=n\) ，就是 \((1,1)\) 加上 \((2,n)\) 再加上 \((1,2)\) 到 \((1,n)\) 的数字和。至此，我们发现这道题的本质就是，你将 \(2n-2\) 个数分为两组，每组 \(n-1\) 个数，使得两组的数字和的最大值最小。这个问题显然可以直接背包，设 \(f_{i,j,k}\) 表示前 \(i\) 个数放 \(j\) 个数在第一组中，第一组的和能否为 \(k\) 。转移显然 \(f_{i,j,k}=f_{i-1,j,k}|f_{i-1,j-1,k-a_i}\) ，答案就是 \(\min_{i=0,f_{2n,n-1,i}=1}^{sum}max(i,sum-i)\) ，此时时间复杂度为 \(O(n^3a)\) 。容易发现 \(f\) 是布尔数组，所以我们可以用 \(bitset\) 去优化转移。时间复杂度为 \(O(\frac{n^3a}{w})\) 。对于输出方案，我们直接利用答案去寻找每个数被放在了哪一组即可。由于数可能为 \(0\) ，实现时可以先将所有数加 \(1\) 最后再减去。

CF1375F Integer Game

​ 交互题。给定三个数 \(a,b,c\) ，先手每次给出一个正整数 \(x\) ，后手需要给这三个数中的某个数加上 \(x\) ，要求不能和上一轮加的数相同，然后告诉先手加的是第几个数。若存在两个数相同先手胜利，若轮数超过 \(1000\) 后手胜利。

​ \(a,b,c\le 10^9\;\;k\le 10^{12}\)

神仙构造题。我们当先手，考虑一个等差数列，我们给后手一个公差，那么如果它最大的那个数不能操作，后手就输了。所以我们考虑如何构造出一个等差数列。我们先令 \(a<b<c\) ，后手给 \(a\) 加上一个数，并使得让 \(a\) 成为最大值，变成 \(b,c,a+x\) ，容易得到要加的数是 \(x=2c-a-b\) ；同理若给 \(b\) 加上 \(2c-a-b\) 也可以。但是若给 \(c\) 加上了，那就不一定了。这启示我们进行一步操作，使后手让一个数变成最大值，这样我们再按照上面的操作，由于后手不能再操作那个最大值了，所以它就能变成一个等差数列了。那我们怎么做呢，很简单，我们直接给一个极大值，例如 \(10^{10}\) ，这样后手无论给谁加上那个数都会变成最大值，然后我们再给一个 \(2c-a-b\) ，它无论给次小值还是最小值，最终都能得到一个等差数列，然后再给一个公差即可。先手仅操作了 \(3\) 次。

AGC010F Tree Game

​ 给定一棵 \(n\) 个点的树，节点 \(i\) 上有 \(a_i\) 个石子。先手会选一个节点并在上面放一个棋子，然后从先手开始，轮流进行操作：从当前棋子所在点上移除一个石子，并将其移到任意一个相邻的节点。若轮到某个人操作时棋子所在的节点上没有石头，那么他输。求出所有可以让先手胜利的初始点。

​ \(n\le 3000\)

考虑初始点 \(u\) ，若相邻节点 \(v\) 满足 \(a_v\ge a_u\) 那么 \(u\) 走到 \(v\) 一定是不优的，因为后手可以从 \(v\) 再移回 \(u\) ，并消耗了 \(u\) 上的石子，一直这么走下去先手就输了，所以他只能去 \(a_v<a_u\) 的节点。而对于后手也同理，它肯定也会去石子个数更少的节点，然后一直走下去直到走到叶子节点而结束。所以我们只需要 \(dfs\) 遍历所有点，求出每个点是必胜态还是必败态即可。实现的好时间复杂度可以为 \(O(n)\) 。（可能给个代码更容易理解 \(dfs\) 的过程）

int a[N];
bool vis[N],f[N];
bool dfs(int u)
{
    if(vis[u]==true) return f[u];
    vis[u]=true;
    for(int i=head[u];i;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(a[v]<a[u])
            if(dfs(v)==false) f[u]=true;
    }
    return f[u];
}

CF1076G Array Game

​ 有 \(n\) 个格子，每个格子上都有一个数 \(a_i\) 。有两种操作，一是将区间 \([l,r]\) 中每个位置上的数加上 \(x\) ，二是查询在区间 \([l,r]\) 游戏的结果。

​ 对于区间 \([l,r]\) 的游戏，起初有一个棋子在 \(l\) 处，并且 \(l\) 处的数减 \(1\) ，双方轮流操作，假设棋子在位置 \(pos\) ，那么一次操作可以将棋子移到 \([pos,pos+m]\) 并且数字大于 \(0\) 的一个位置，再将这个位置上的数减 \(1\) 。最后不能操作的人输。

​ \(n,q\le 2\times 10^5\;\;m\le 5\;\;x,a_i\le 10^{12}\)

先考虑这个游戏，容易发现对于 \(a_i\) 我们只关心它的奇偶性，因为如果先手呆在这个点不动，那么后手显然也可以呆在这个点不动，直到 \(a_i<2\) ，所以我们直接将所有的 \(a_i\) 先模个 \(2\) 。我们考虑什么时候会获胜，我们定义 \(f_{i,0/1}\) 表示位置 \(i\) 分别为 \(0/1\) 时的输赢状态，\(0\) 表示先手输，\(1\) 表示先手赢。若 \(f_{i,j}=1\) ，那么一定存在某个位置 \(k\in[i+1,min(i+m,n)]\) 使得 \(f_{k,a_k}=0\) ，或者 \(j=1\) 并且 \(f_{i,0}=0\) ，通过我们可以呆在原地不动一次即可。剩下的情况 \(f\) 值均为 \(0\) 。至此我们可以得到一个暴力的 \(dp\) 做法。

考虑优化，首先此题涉及到区间操作，我们可以利用线段树，同时我们发现 \(m\) 非常小。我们重新设一个东西，我们对于每个线段树上的区间 \([l,r]\) 设 \(f_{i}\) 表示 \([r+1,r+m]\) 中第一个必败态的位置为 \(r+i\) 时，\([l,l+m-1]\) 中第一个必败态的位置为 \(l-1+f_i\) ，正常范围为 \([1,m]\) ，若为 \(m+1\) 则表示不存在必败态。容易发现这个区间信息很容易维护，假设左区间为 \(fl\) ，右区间为 \(fr\) ，合并完为 \(f\) ，那么 \(f_i=fl_{fr_i}\) ，\(fl_{fr_i}\) 表示 \([r+1,r+m]\) 中第一个必败态的位置为 \(r+i\) ，\([mid+1,mid+m]\) 中第一个必败态的位置为 \(fr_i\) ，那么对于区间 \([l,mid]\) ，\(fl_{fr_i}\) 为 \([l,l+m-1]\) 中第一个必败态的位置，合并完毕。由于与数的奇偶性有关，每次区间加 \(x\) ，当 \(x\) 为偶数时奇偶性不发生改变，奇数时改变，所以我们还要维护一个翻转后的 \(f\) 和一个翻转的懒标记。

然后说一些细节 ，对于单个位置 \(pos\) ，容易得到初始时 \(f_i=i+1\) ，对于 \(a\) 值为奇数和偶数的 \(f\) 要分开处理。对于查询操作，我们区间查询时得到的 \(f\) ，我们只需要判断 \(f_{m+1}\) 是否为 \(1\) 即可，因为 \(f_{m+1}\) 表示 \(r\) 后面没有必输态，也就相当于不存在后面的位置，如果是 \(1\) 那么 \(l\) 就是必输态，否则不是。时间复杂度为 \(O(qm\log n)\) 。

CF1149E Election Promises

​ 有一个 \(n\) 个点 \(m\) 条边的有向无环图，初始每个点有一个值 \(a_i\) 。先后手轮流操作，每次可以选一个点，将这个点的值减少为一个非负整数，然后可以任意改变和这个点直接相连的点上的值，要求改之后还是非负整数，无法进行操作的人输，保证游戏会结束。若两人都使用最优策略，问先手胜还是后手胜，若先手胜还要输出先手第一次操作后每个点上的值。

​ \(n,m\le 2\times 10^5\)

我们先给每个点定义一个权值 \(val\) ，设 \(val_u=mex\lbrace val_v\rbrace\) ，要求存在有向边 \(u\) 到 \(v\) 。

• Lemma 1 ：对于任意一条 \(u\) 到 \(v\) 的边，\(val_u\ne val_v\) 。

根据 \(val\) 的定义显然可以得到。

• Lemma 2：我们设 \(F(x)\) 表示所有 \(val_u=x\) 的节点 \(u\) 的值的异或和。那么若对于所有 \(x\) 均满足 \(F(x)=0\) ，那么在操作一次后，一定存在一个值 \(p\) 满足 \(F(p)\ne 0\) 。

我们设操作的点为 \(u\) ，根据 Lemma 1 \(F(val_u)\) 的值只会被点 \(u\) 所影响，因为直接相连的点的 \(val\) 均不等于 \(val_u\) ，所以 \(a_u\) 减少后，\(F(val_u)\) 一定就不为 \(0\) 了。

• Lemma 3：若存在一个 \(p\) 满足 \(F(p)\ne 0\) ，那么一定存在一种操作使得操作后所有的 \(x\) 均满足 \(F(x)=0\) 。

我们假设 \(y\) 为所有满足 \(F(y)\ne0\) 中最大的一个数。我们考虑 \(val_u=y\) 的点 \(u\) ，若我们想让 \(F(y)=0\) ，我们要将 \(a_u\) 修改为 \(F(y)\bigoplus a_u\) ，那我们现在又需要证明，一定存在一个点 \(u\) 使得 \(val_u=y\) 且 \((F(y)\bigoplus a_u)<a_u\) 。

我们考虑 \(F(y)\) 的二进制位下最高的那个 \(1\) ，由于 \(F(y)\) 是所有 \(val_u=y\) 的节点 \(u\) 的 \(a_u\) 的异或和。那么一定存在一个 \(u\) 满足 \(a_u\) 的那一位也是 \(1\) ，我们让这个 \(a_u\) 异或上 \(F(y)\) 得到新的 \(a_u\) ，新的 \(a_u\) 那一位一定是 \(0\) ，且那一位的前几位也一定不会变化，因为找的是 \(F(y)\) 二进制下最高位的那个 \(1\) ，那么 \(F(y)\) 最高位前面的那几位肯定都是 \(0\) ，异或完不会改变。所以新的 \(a_u\) 就一定会小于原来的 \(a_u\) ，证毕。

那么我们已经将 \(F(y)\) 修改为 \(0\) ，而根据 \(val\) 的定义，那么对于所有小于 \(y\) 的数 \(z\) ，满足 \(val_u=y\) 的节点 \(u\) 一定会有直接相连的点 \(v\) 满足 \(val_v=z\) 。由于我们可以任意修改与 \(u\) 直接相连的节点 \(v\) ，那么我们将 \(a_v\) 修改为 \(F(val_v)\bigoplus a_v\) 即可，这样所有的 \(F\) 值就能变成 \(0\) 了，证毕。

• Lemma 4：先手胜利当且仅当存在一个 \(x\) 满足 \(F(x)\ne 0\) 。

若一开始存在 \(x\) 满足 \(F(x)\ne 0\) ，那么根据 Lemma 3 先手可以一次操作把所有 \(F\) 值变为 \(0\) 。而根据 Lemma 2 后手操作完后一定会存在一个 \(x\) 满足 \(F(x)\ne 0\) 。所以先手操作完一定是 \(F\) 值都是 \(0\) 的局面，后手操作完一定是存在 \(F(x)\ne 0\) 的局面。由于结束局面是所有节点的值都是 \(0\) ，那么结束局面显然就是所有的 \(F\) 值都是 \(0\) ，是先手操作完得到的，那么此时后手就无法操作了，先手胜利。相反后手胜利。

我们 \(dfs\) 一遍容易求出所有点的 \(val\) ，进而求出初始所有的 \(F\) 值，就可以判断先手胜利还是后手胜利了。对于先手胜利，我们按照 Lemma 3 从大到小枚举找到第一个 \(F\) 值不为 \(0\) 的，然后根据上面所说的直接模拟即可。时间复杂度为 \(O(n)\) 。

CF1110G Tree-Tac-Toe

​ 给定一棵 \(n\) 个点的树，初始时有的节点是白色，有的节点没有颜色。有两个人在树上游戏，先手每轮可以将一个没有颜色的点染成白点，后手每轮可以将一个没有颜色的点染成黑点。若某人染色后，树上存在三个点 \(u,v,z\) 满足 \(u\) 到 \(v\) ，\(v\) 到 \(z\) 均有边，并且 \(u,v,z\) 三个点都有颜色且颜色相同，那么该颜色对应的人获胜。假设两人都很聪明，问游戏结果。

​ \(n\le 5\times 10^5\)

我们先考虑初始树上所有点都没有颜色的情况。显然后手是不可能胜利的，因为他的胜利策略肯定会先被先手走到。所以我们考虑什么时候先手是可以获胜的。

注意到若所有点的度数都 \(\le 2\) ，那么这颗树是一条链，显然是平局。所以我们只考虑度数大于 \(2\) 的点的情况。

• 存在某个节点的度数 \(\ge 4\)

先手只需要占到那个点即可，剩下四个点先手可以占两个，先手获得胜利。

• 存在度数为 \(3\) 的点，并且它至少有两个儿子度数 \(\ge 2\)

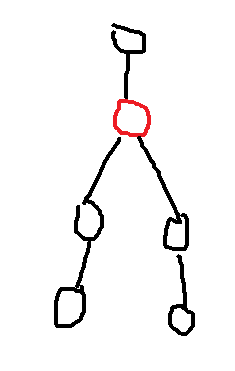
假设只有一个儿子度数大于 \(2\) ，先手占到那个点后，后手一定会把这个度数 \(\ge2\) 的儿子占掉，此时这个点只剩两个儿子，并且度数都是 \(1\) ，也就是没有连其它的点，那么先手占掉一个后手再占掉一个先手就无法胜利。

若至少两个儿子度数 \(\ge 2\) ，后手只能占到一个，先手占到另一个即可，这样无论后手占哪个都会留下点给先手，从而先手获得胜利。

• 存在两个度数为 \(3\) 的点，之间的路径长度为偶数

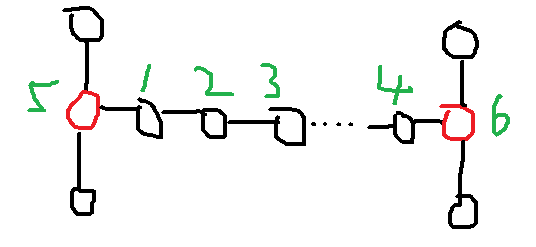
先手先占 \(1\) 号点，后手肯定会占 \(5\) 号点，然后先手不断去占距离上次的点距离为 \(2\) 的点（图中是 \(3\) 号点），后手就会占中间夹得那个点（图中是 \(2\) 号点），不断这么做下去，最后先手可能占到 \(4\) 号点也可能占到 \(6\) 号点。若占到 \(4\) 号点，后手就会去占 \(4\) 号点左边的点，先手占 \(6\) 号点即可获胜。若占到 \(6\) 号点，那么先手占 \(4\) 号点，先手无法获胜。容易发现若两点距离为偶数是先手获胜。

• 度数为 \(3\) 的节点数量大于 \(2\)

若数量大于 \(2\) ，我们从中找 \(3\) 个点，一定会满足一点在另外两个点的路径上，设两点距离分别为 \(x,y,z\) ，那么 \(x+y=z\) ，容易得出这三个数中一定有偶数，那么它就会满足上一种情况，所以先手会胜利。

以上就是没有初始颜色时的情况，我们考虑如何处理初始的那几个白色节点。我们可以考虑转化为一般的情况，我们对于初始为白色的点，我们可以把它看成原来空的一个节点，然后先手占了它，而后手下在了原图之外的点，也就是我们对这个点进行拆点，让后手一定要下在拆出的点上，我们考虑如何拆点能让后手一定能占在拆出的点上。很简单，我们只要如下图所示。

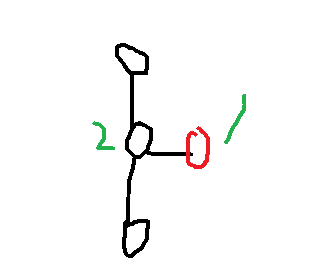
我们令 \(1\) 号点为初始颜色是白色的点，我们这样拆点后，后手一定会占 \(2\) 号点。由于下面三个点是新加出来的点，所以它们不会影响到原来树上的点，此时就相当于 \(1\) 号点原先就是白色的。所以我们拆完点之后就可以按照上述判断方法去判断是先手胜利还是平局了。时间复杂度为 \(O(n)\) 。

AGC010E Rearranging

​ 给定一个长度为 \(n\) 的序列 \(a\) ，先手可以将序列任意排列，后手可以任意次交换两个相邻位置的互质的数。先手想要最终序列的字典序尽量小，后手想要最终序列的字典序尽量大。求最终的序列。

​ \(n\le 2000\;\;a_i\le 10^{18}\)

容易发现后手无法改变两个不互质的数之间的相对位置。我们不妨对 \(i<j\) 且 \(gcd(a_i,a_j)\ne 1\) 的 \(i\) 和 \(j\) 之间连一条无向边，这样会得到若干个连通块。由于先手可以任意排列，就相当于对这些连通块中的边定向，\(i\) 到 \(j\) 的有向边就表示 \(a_i\) 在 \(a_j\) 前面，从而使得每一个连通块都形成 \(DAG\) ，并且还要求字典序最小。我们可以将原序列从小到大排序，方便我们操作。我们从 \(1\) 到 \(n\) 去枚举点 \(u\) ，然后 \(dfs\) ，每次我们从 \(1\) 到 \(n\) 去枚举与 \(u\) 有边的点 \(v\) ，若 \(v\) 没遍历过我们就可以贪心地连一条从 \(u\) 到 \(v\) 的有向边。这样我们就可以得到先手操作后的最优序列。

我们再考虑后手的操作，如果他想得到任意一个满足要求的序列，只需要对先手定完向的图进行拓扑排序即可。若后手想要字典序最大，很简单，只需要将拓扑排序的一般队列换成大根堆即可。时间复杂度为 \(O(n^2\log a)\) 。

CF294C Shaass and Lights

​ 有 \(n\) 盏灯，有 \(m\) 盏已经点亮，并给出这 \(m\) 盏灯的编号。每次只能点亮一盏与已经点亮的灯相邻的灯，求点亮所有灯的方案数对 \(10^9+7\) 取模的结果。

​ 原题：\(1\le m\le n\le 10^3\) 事实上可以：\(1\le m\le n\le 10^6\)

考虑如何转化题意。我们可以以原先已经点亮的灯为分界线，这样序列就会分成 \(m+1\) 段，我们设第 \(i\) 段的长度为 \(l_i\) 。每次我们只能一段中最左边的灯或最右边的灯，注意第 \(1\) 段只能点亮最右边，第 \(m+1\) 段只能点亮最左边。我们考虑将其转化成操作序列的计数，假如我们先不考虑左右方向，容易得出这是一个多重集排列数，方案数为：

我们再考虑上方向，对于 \(2\) 到 \(m\) 的每一段，总共点亮 \(l_i\) 次。而除了最后一次点亮，其它都有两种操作方式，即点亮左边或点亮右边。综合上面可以得到最终的答案式子：

预处理 \(2\) 的幂次以及阶乘的逆元，时间复杂度为 \(O(n)\) 。

AGC020C Median Sum

​ 给定一个长度为 \(n\) 的序列 \(a\) ，求它的所有非空子序列的和的中位数。

​ \(n,a_i\le 2000\)

巧妙题。我们不妨设 \(sum=\sum_{i=1}^{n}a_i\) ，假如我们考虑上空序列，那么任意一个和为 \(x\) 的子序列，都会有一个和为 \(sum-x\) 的子序列与其对应，同时 \(x\) 和 \(sum-x\) 中，一定有一个 \(\le \frac{sum}{2}\) ，另一个 \(\ge \frac{sum}{2}\) 。此时再去掉空序列的和 \(0\) 并从小到大排序后，容易发现中位数就是所有数中第一个 \(\ge \lceil\frac{sum}{2}\rceil\) 的数。

这样我们就可以想到一个 \(dp\) ，设 \(f_{i,j}\) 表示前 \(i\) 个数能否组成数字 \(j\) ，转移显然：\(f_{i,j}=f_{i-1,j}|f_{i-1,j-a_i}\) 。最后我们直接从 \(\lceil\frac{sum}{2}\rceil\) 枚举答案即可。去掉第一维并使用 \(bitset\) 优化，时间复杂度为 \(O(\frac{n^2a}{w})\) 。

ARC112E Cigar Box

​ 给定一个 \(1\) 到 \(n\) 的排列 \(p\) 。要求进行 \(m\) 次操作，每次操作可以将排列中的任意一个数移到第一位或最后一位，求将序列 \(1,2,3\cdots ,n\) 变成排列 \(p\) 的操作方案数对 \(998244353\) 取模后的结果。

​ \(2\le n\le 3000\;\;1\le m\le 3000\)

考虑最终一个数的位置，只会与这个数的最后一次操作有关。我们定义每个数的最后一次操作为有用操作。我们不妨设有 \(l\) 个有用操作是将数移到第一位，\(r\) 个操作是将数移到最后一位，我们容易发现 \(l+1\) 到 \(n-r\) 这段位置上的数的相对大小是没有改变的，换句话说，\(l+1\) 到 \(n-r\) 位置上的数最后一定是单调递增的，这是一个很重要的性质。此时我们考虑如何对操作序列计数，容易想到我们设 \(f_{i,l,r}\) 表示当前共进行了 \(i\) 次操作，\(l\) 次有用操作是将数移到第一位，\(r\) 次有效操作是将数移到最后一位。这个 \(dp\) 其实是按照时间顺序从后往前填充操作序列的。转移时我们考虑对第 \(i+1\) 次操作进行分类：

• 第 \(i\) 次操作为无效操作，它可以放在任意一次有效操作的前面或后面，那么有 \(f_{i+1,l,r}+=f_{i,l,r}\times 2\times (l+r)\)
• 第 \(i\) 次操作为有效操作，按照移到第一位还是最后一位分类可以得到，\(f_{i+1,l+1,r}+=f_{i,l,r}\) ，\(f_{i+1,l,r+1}+=f_{i,l,r}\)

但此时时间复杂度为 \(O(n^3)\) 。我们考虑如何优化转移。容易发现转移中对 \(l,r\) 的具体值我们并没有太关心，我们只关心 \((l+r)\) 的值，所以我们不妨将状态改为：设 \(f_{i,j}\) 表示当前共进行了 \(i\) 次操作，共 \(j\) 次有效操作。转移显然页变为：\(f_{i+1,j}+=f_{i,j}\times 2\times j\) ，\(f_{i+1,j+1}+=f_{i,j}\) 。此时转移时间复杂度已经成为 \(O(n^2)\) 。

最后我们考虑答案的统计，我们先从小到大枚举 \(l\) ，再从 \(n-l\) 到 \(0\) 枚举 \(r\) 。还记得前面说的那个性质吗，我们还需要判断是否单调递增，其实就是当 \(a_{n-r-1}>a_{n-r}\) 就 \(break\) 即可。我们再考虑 \(f_{i,j}\) 对操作序列数量的贡献系数，就相当于确定这 \(j=l+r\) 次操作的顺序，那么其实就是 \(\binom{l+r}{l}\) 。直接预处理组合数，总时间复杂度为 \(O(n^2)\) 。

AGC021F Trinity

​ 有一个 \(n\) 行 \(m\) 列的表格，每个格子只能为黑色或白色。对于一个 \(n\times m\) 的表格，我们生成长度为 \(n\) 的序列 \(A\) 以及长度为 \(m\) 的序列 \(B,C\) 。其中 \(A_i\) 表示第 \(i\) 行第一个黑色格子的列编号，若没有则为 \(m+1\) ；\(B_i\) 表示第 \(i\) 列第一个黑色格子的行编号，若不存在则为 \(n+1\) ；\(C_i\) 表示第 \(i\) 列第一个黑色格子的行编号，若不存在则为 \(0\) 。求出所有 \(2^{nm}\) 种表格中，不同的数列三元组 \((A,B,C)\) 对 \(998244353\) 取模后的结果。

​ \(1\le n\le 8\times 10^3\;\;1\le m\le 200\)

神仙计数题。我们考虑设 \(f_{i,j}\) 表示当前 \(dp\) 到第 \(j\) 列，前 \(j\) 列恰好有 \(i\) 行满足至少有一个黑色格子时，数列三元组 \((A,B,C)\) 的数量。转移时考虑枚举前 \(j-1\) 列中恰好满足至少有一个黑色格子的行数 \(k\) ，此时要对 \(k\) 分个类。

• \(k=i\)

由于 \(A\) 序列记录的是第一个黑色格子的位置，那么容易发现新增第 \(j\) 列后 \(A\) 序列是不会改变的。我们再考虑第 \(j\) 列第一个黑色格子和最后一个黑色格子的位置。若第 \(j\) 列没有黑色格子，此时为单独一种情况；若有黑色格子，显然有 \(B_j\le C_j\) （其中 \(B_j=C_j\) 表示这一列只有一个黑色格子），并且只有 \(i\) 行可以为黑色格子，容易得出方案数为 \(B_j=C_j\) 的 \(i\) 种加上 \(B_j<C_j\) 的 \(\binom{i}{2}\) 种。

• \(k<i\)

此时会有 \(i-k\) 行在第 \(j\) 列上新出现了黑色格子，原来 \(k\) 行任意。此时这 \(i-k\) 行的 \(A\) 值就均变成了 \(j\) ，而其它行仍没有变，所以 序列 \(A\) 对方案数仍然没有影响。我们主要考虑 \(B,C\) 的数量，有一个比较显然的想法就是选择黑色格子的方案数 \(\binom{i}{i-k}\) ，但显然它是错误的，因为 \(B_j,C_j\) 也与原来 \(k\) 行在第 \(j\) 列是否为黑色格子有关。我们不妨换一个角度统计，考虑第一个黑色格子前面的白色格子即第 \(B_j-1\) 行，以及最后一个黑色格子的后面的白色格子即第 \(C_j+1\) 行，再加上中间 \(i\) 行，总共是 \(i+2\) 行。我们要从中选出 \(i-k+2\) 行，来作为出现黑色格子的 \(i-k\) 行以及作为 \(B_j-1,C_j+1\) 的两行，方案数即为 \(\binom{i+2}{i-k+2}\) 。

两种情况综合起来我们就可以得到转移：\(f_{i,j}=f_{i,j-1}\times (1+i+\binom{i}{2})+\sum_{k=0}^{i-1}f_{k,j-1}\times \binom{i+2}{i-k+2}\) 。此时时间复杂度为 \(O(n^2m)\) ，我们还需要优化。

我们单独拿出来后面那个转移，\(\sum_{k=0}^{i-1}f_{k,j-1}\times \binom{i+2}{i-k+2}=(i+2)!\sum_{k=0}^{i-1}f_{k,j-1}\frac{1}{(i-k+2)!k!}=(i+2)!\sum_{k=0}^{i-1}\frac{f_{k,j-1}}{k!}\frac{1}{(i-k+2)!}\) 容易发现这竟然是和卷积形式，直接 \(NTT\) 卷一下即可，时间复杂度降为 \(O(nm\log n)\) 。

答案统计也很简单，只需要考虑选出那 \(i\) 行的方案数即可，即 \(ans=\sum_{i=0}^{n}\binom{n}{i}f_{i,m}\) 。

CF1152F1&F2 Neko Rules the Catniverse

​ 给定 \(n,m,k\) ，求满足以下条件的长度为 \(k\) 的序列的个数对 \(10^9+7\) 取模后的结果。

• 任意两个位置的数不同
• 每个位置上的数 \(\ge 1\) 且 \(\le n\)
• 对于所有 \(2\le i\le n\) 满足 \(a_i\le a_{i-1}+m\)

​ \(1\le k\le min(n,12)\;\; 1\le m\le 4\) F1：\(1\le n\le10^5\) F2：\(1\le n\le 10^9\)

我们可以先套路性地设 \(f_{i,j}\) 表示值域 \([1,n]\) 中前 \(i\) 个数中选择 \(j\) 个数放入序列的方案数。如果不选 \(i\) 很好转移，但如果选择 \(i\) ，由于有第三条限制，此时并不容易转移。但我们又可以发现只有值在 \([i-m+1,i]\) 中的位置的后一位才可能放 \(i\) 并参与方案数的统计，并且 \(m\) 很小，我们不妨直接状压并新增一维 \(S\) 表示 \([i-m+1,i]\) 的选择情况为 \(S\) ，\(S\) 是一个长度为 \(m\) 的二进制数，若这个数已经用过用 \(1\) 表示否则用 \(0\) 。此时转移方程就很显然了，若我们不选择 \(i\) 这个数，我们从 \(i-1\) 的状态 \(S\) ，要先乘 \(2\) 来多记录数 \(i\) 的状态，同时为了保持长度为 \(m\) ，我们还要删去第一位的状态，其实就是：

同理若选 \(i\) ，由于我们可以将 \(i\) 放在值在 \([i-m+1,i]\) 中的位置的后一位，那么方案数就是 \(S\) 二进制下 \(1\) 的个数，并且它可以放在最前面，所以总放置 \(i\) 的方案数就是 \(popcount_S+1\) ，而转移后 \(S\) 的变化与上面类似，整理得到：

答案就是枚举状态 \(S\) 将 \(f_{n,k,S}\) 加起来即可，此时时间复杂度为 \(O(nk2^m)\) ，可以通过 F1 。

容易发现每次是由 \(f_{i-1}\) 转移到 \(f_i\) ，所以我们直接上矩阵快速幂优化转移即可，将两维 \(j,S\) 压成一维直接跑即可，此时矩阵边长为 \(k\times 2^m\) ，时间复杂度为 \(O(k^38^m\log n)\) ，可以通过 F2 。

CF660E Different Subsets For All Tuples

​ 求出：长度为 \(n\) 且每个位置上的值在 \([1,m]\) 范围内的每个序列中本质不同的子序列个数对 \(10^9+7\) 取模后的结果。

​ \(n,m\le 10^6\)

我们先单独考虑空子序列的个数 \(m^n\) 。我们考虑枚举子序列的长度 \(i\) ，这样的子序列有 \(m^i\) 种。我们考虑在子序列种插入一些数来还原得到长度为 \(n\) 的序列，同时为了不重复计算，我们钦定该子序列在所有与它本质相同的子序列中出现下标的字典序最小。此时假设我们的子序列在原序列中的下标分别为 \(pos_1,pos_2,\cdots ,pos_i\) ，值分别为 \(v_1,v_2,\cdots v_i\) ，那么 \(pos_1\) 前面不能出现与 \(v_1\) 相等的数字，\(pos_1+1\) 到 \(pos_2-1\) 之间不能出现与 \(v_2\) 相等的数字，依次类推。最终到 \(pos_i\) 后面就可以随便填那 \(m\) 种数字了。事实上到这里我们就可以得出式子了：

其中 \(i\) 是枚举子序列的长度，\(m^i\) 是子序列的数量，\(j\) 是枚举的 \(pos_i\) 的值，而 \(pos_1\) 到 \(pos_{i-1}\) 的值可以在 \(1\) 到 \(pos_i-1=j-1\) 之间任选，方案数就是 \(\binom{j-1}{i-1}\) 。然后 \(1\) 到 \(pos_i-1\) 这些位置中，除了 \(pos_1,pos_2,\cdots pos_{i-1}\) 这 \(i-1\) 个位置的值确定了，其它 \(j-1-(i-1)=j-i\) 个位置的值，都要满足上面与对应的 \(v\) 不同的哪个限制，也就是能取到的值都只有 \(m-1\) 种，所以这一段方案数为 \((m-1)^{j-i}\) ，而 \(pos_i+1\) 到 \(n\) 的这 \(n-j\) 个位置都可以有 \(m\) 种取值，方案数为 \(m^{n-j}\) 。乘起来就可以得到上面的式子。我们接下来考虑化简。

预处理 \(m\) 和 \(2m-1\) 的幂次，时间复杂度为 \(O(n)\) 。答案别忘了加上空子序列的 \(m^n\) 。

[PKUSC2018] 最大前缀和

​ 给定一个长度为 \(n\) 的序列 \(a\) ，现将序列随机打乱，求打乱后的序列的最大前缀和的期望值乘上 \(n!\) 对 \(998244353\) 取模后的结果。

​ \(1\le n\le 20\;\;\sum |a_i|\le 10^9\)

我们不妨去考虑最大前缀和的性质。我们假设 \(\sum_{i=1}^{p}a_i\) 为最大前缀和，那么它需要满足：

• 不存在 \(1< x\le p\) 满足 \(\sum_{i=x}^{p}a_i\) 小于 \(0\) ，否则我们直接删去这一段后缀答案更大。
• 不存在 \(p<x\le n\) 满足 \(\sum_{i=p+1}^{x}a_i\) 大于 \(0\) ，否则我们再选上这一段前缀答案更大。

容易发现两个条件正好被 \(p\) 所分开，所以我们分别进行 \(dp\) 。我们先设 \(f_S\) 表示集合 \(S\) 是最大前缀和时集合 \(S\) 的序列满足第一个条件的方案数，全集为 \(U\) ，\(g_{U-S}\) 表示集合 \(S\) 是最大前缀和时集合 \(U-S\) 的序列满足第二个条件的方案数（\(U-S\) 其实就是 \(S\) 的补集），\(sum_S\) 表示集合 \(S\) 中所有元素之和。

我们让 \(g\) 是从前面往后面加数，那么显然我们枚举不在 \(S\) 中的元素 \(x\) ，设 \(x\) 加入集合 \(S\) 后变成集合 \(T\) ，由于是从前往后加数，那么只需判断前缀和是否小于 \(0\) 。其实就是若 \(sum_T<0\) 我们就有 \(g_T+=g_S\) 。

同理我们让 \(f\) 是从后面往前面填数，但如果单纯按照 \(g\) 的转移事实上是有问题的。因为在条件一中，我们有 \(x\ne 1\) ，也就是说这个后缀不能是它本身。所以直接那么做会有一些问题，那么我们不妨再记一维 \(0/1\) ，\(0\) 表示 \(sum_S<0\) 并满足条件一的情况，\(1\) 表示 \(sum_S\ge 0\) 并满足条件一的情况。将 \(x\) 加入集合后，为了满足条件一，那么 \(f_{T}\) 就只能从 \(f_{S,1}\) 转移过来了。而至于是 \(f_{T,0}\) 还是 \(f_{T,1}\) 直接看 \(sum_T\) 与 \(0\) 的大小关系即可。

此时我们就完成了转移，答案显然就是 \(\sum_{S\subset U}(f_{S,0}+f_{S,1})\times g_{U-S}\times sum_S\) 。时间复杂度为 \(O(2^nn)\) 。

CF1716F Bags with Balls

​ 有 \(n\) 个有标号袋子，每个袋子里有标号为 \(1\) 到 \(m\) 的球各一个。需要从每个袋子里选一个球，设最终标号为奇数的球的数量为 \(x\) 。求出所有取球方案的 \(x^k\) 之和对 \(998244353\) 取模后的结果。

​ \(1\le T\le 5000\;\;n,m\le 998244352\;\;k\le 2000\)

显然是枚举最终标号为奇数的球的数量为 \(i\) ，然后计算有多少种取球方式可以得到，我们先假设 \(1\) 到 \(m\) 中奇数的个数为 \(x\) 。显然会有 \(i\) 个袋子取出标号为奇数的球，方案数为 \(\binom{n}{i}\) 。对于这 \(i\) 个袋子，每个袋子都有 \(x\) 种取出奇数的方案，方案数为 \(x^i\) 。同理对于剩下 \(n-i\) 个袋子每个袋子都有 \(m-x\) 种取出偶数的方案，方案数为 \((m-x)^{n-i}\) 。合并在一起可以得到答案式子：

我们大力化简式子：

直接 \(O(k^2)\) 预处理第二类斯特林数即可，单次计算时间复杂度为 \(O(k)\) 。总时间复杂度为 \(O(k^2+Tk)\) 。

[HNOI2012] 集合选数

​ 给定 \(n\) ，求集合 \(\lbrace1,2,3,\cdots,n\rbrace\) 中满足以下条件的子集个数对 \(10^9+1\) 取模后的结果。

若元素 \(x\) 在子集中，那么 \(2x\) 和 \(3x\) 均不能在子集中。

​ \(n\le 10^5\)

考虑如何转化 \(2x\) 和 \(3x\) 不能在子集中的这个限制。我们考虑构造一个矩形，第一行第一列的元素为 \(1\) ，然后每一行后一个数均为前一个数的 \(2\) 倍，每一列后一个数都是前一个数的 \(3\) 倍。构造矩形完毕后，题意其实就变成在这个矩形中选出一些数，并且要求相邻的数不能同时选择的方案数。由于长为 \(log_2n\) 宽为 \(log_3n\) ，所以我们可以直接使用状压 \(dp\) 求解。

但是容易发现 \(1\) 到 \(n\) 中不是所有数都会出现在矩形中，所以我们对于没出现在矩形中的数（事实上就是既不是 \(2\) 的倍数又不是 \(3\) 的倍数的数），都拿它作为新矩形的左上角元素重新进行填充，并不断对新的矩形继续求解即可。根据乘法原理，答案就是所有矩形的答案乘在一起。时间复杂度不会计算，反正可以通过。

[省选联考 2021] 滚榜

​ 初始有 \(n\) 支队伍，每支队伍的过题数为 \(a_i\) 。排行榜上按照队伍的过题数从大到小排名，若题数相同则编号小的在前。同时每支队伍的新过题数为 \(b_i\) ，也就是说这支队伍的总过题数为 \(a_i+b_i\) 。现在按照 \(b_i\) 不降的顺序依次公布每支队伍的新过题数，并且每公布一支队伍，排行榜就会实时更新排名。并且满足每公布一支队伍的新过题数后，这支队伍都成为了新排行榜上的第一名。已知 \(\sum_{i=1}^{n}b_i=m\) ，求最终排行榜上队伍的排名情况可能有多少种。

​ \(n\le 13\;\;m\le 500\)

我们先考虑一个暴力，枚举最终的排名，排名从大到小排序就可以得到公布的顺序，然后检验其是否合法。显然我们可以贪心地分配给每支队伍最少的题使得它变成第一。具体地，若 \(a_i>a_{i-1}\) ，我们只需要满足 \(b\) 单调不降即可，有 \(b_i=b_{i-1}\) ；否则我们需要至少给 \(a_i\) 分配 \(a_{i-1}+b_{i-1}-a_i\) 才能使 \(i\) 变成第一。最终直接判断和是否超过 \(m\) 即可，时间复杂度为 \(O(n!\times n)\) 。

容易发现按照上面的策略，我们可以得到式子：\(\sum_{i=1}^{n}b_i=max(a_{i-1}-a_i,0)\times (n-i+1)\) 。只需考虑对后面的贡献次数就能得到，然后比较这个式子和 \(m\) 的大小即可。这个式子对正解有帮助。

看到 \(n\) 这么小，我们不妨考虑状压 \(dp\) 。考虑状态，肯定还要记录上一个公布的队伍是哪个，我们再记录上述式子的值。即设 \(f_{S,i,j}\) 表示已公布的状态为 \(S\) ，这一次公布的是第 \(i\) 支队伍，现在上述式子的值为 \(j\) 的方案数。转移只需考虑枚举这一次选择的队伍、下一次选的队伍以及上述式子的值即可。答案就是 \(\sum_{i=1}^{n}\sum_{j=0}^{m}f_{U,i,j}\) ，其中 \(U\) 表示全集。最终时间复杂度为 \(O(2^nn^2m)\) 。注意题数相同按照编号排序的规则，上述转移中自动忽略了。

[SNOI2017] 礼物

​ 有递推式：\(f_i=s_{i-1}+i^k,s_i=s_{i-1}+f_i\) ，求 \(f_n\) 的值，对 \(10^9+7\) 取模。

​ \(n\le 10^{18}\) ， \(1\le k\le 10\) 。

标算是矩阵快速幂，但已经爆标，可以做到 \(O(k^2)\) 或 \(O(k\log k)\) 。

显然这个递推式可以改写成：\(s_i=s_{i-1}+s_{i-1}+i^k=2s_{i-1}+i^k\) ，我们只需要求 \(f_n=s_{n-1}+n^{k}\) ，所以我们主要考虑如何求 \(s_{n-1}\) 。以下设 \(m=n-1\) 。

容易发现 \(s_m=\sum_{i=0}^{m}2^{m-i}i^k\) ，我们利用自然数幂转化成第二类斯特林数的套路进行化简。

我们设 \(g_j=\sum_{i=j}^{m}2^{m-i}\binom{i}{j}\) ，那么 \(s_m=\sum_{j=0}^{k}j! {k \brace j}g_j\) ，我们尝试寻找 \(g\) 的一个递推式。

初始化 \(g_0=\sum_{i=0}^{m}2^{m-i}=2^m+2^{m-1}+\cdots+2^0=2^{m+1}-1\) ，此时可以递推求出 \(g\) 的每一项。

此时时间复杂度为 \(O(k^2)\) 或 \(O(k\log k)\) ，取决于预处理第二类斯特林数的方法，由于只需要同一行的斯特林数，所以可以用多项式优化到 \(O(k\log k)\) 。