学习笔记——凸包
还没写完
今天上午去蹭楼下新高一多校联训的课,讲的计算几何,听到的。
顺带一提,楼下多校联训的讲课速度极度抽象
感觉就像不到两月AK NOI 知识点。
他们已经讲了相当一些我们没来得及学的东西了。
绷
先大概说说啥是计算几何
一句话就是用计算机解决几何问题
可能有的数学大神会觉得没必要,
但事实上,生活中的几何问题远比几个图形复杂,
所以对于这些复杂而抽象的问题,我们需要计算机。
于是,有了计算几何。
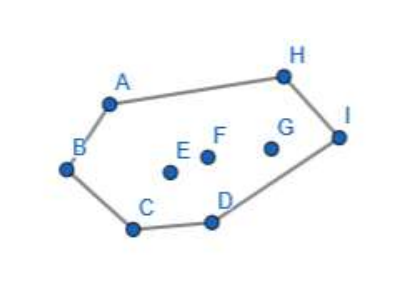
在平面上能包含所有给定点的最小凸多边形叫做凸包.
其定义为,对于给定集合 X所有包含 X 的凸集的交集 S 被称为 X 的凸包.
----OI Wiki
可以理解成,我们用一根橡皮筋把所有给定的点包住。
特别的,凸包一定是用最小的周长包住所有给定点。
如果凸包的形状是一个凹多边形,它的周长一定不是最优的,
因为我们一定可以不让凸包的边缘向内凹,形成一个凸多边形——这样才有最优的边长。
如图。
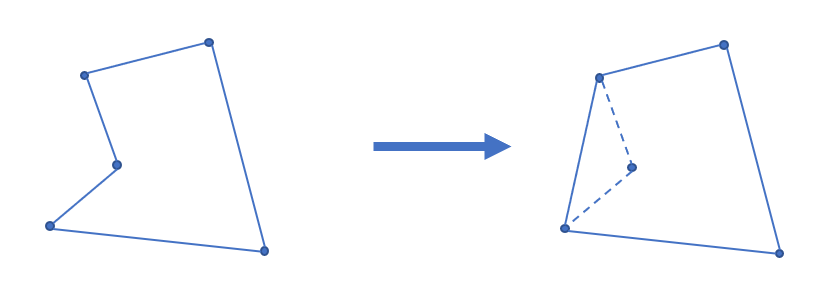
所以,我们可以用另一句话形容凸包:
覆盖平面上若干个点的周长最小的凸多边形。
但是显然啊,我们的计算机不会自己找这种特殊的凸多边形。它无法模拟橡皮筋的收缩过程。
于是有了下文。
求二维凸包
我们要维护一个凸壳。(可以感性理解为所求凸包最外圈的一部分)
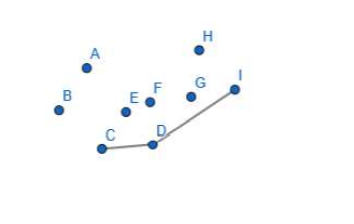
先找到左下角的那个点(优先考虑最下,保证纵坐标一定是最小的),记为P1
以P1为原点,对P2~Pn按横坐标排序
也可以按极角排序(可以感性理解为一个点与x轴的夹角)
但是不用把极角算出来(我不会),直接按叉积排序就行。
刚才强调P1是最左下的点,是因为这样的话其他的点都在以其为原点的坐标系的一二象限,从而保证P0在凸包上
(第二象限是左上角那个,应该不会有人像我一样突然搞混了吧)
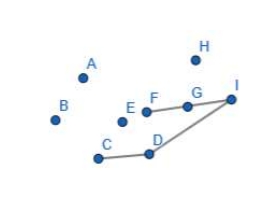
如图。先把C,D,I入栈。
然后按顺序枚举其他点。从G开始,观察D-I-G三个点,发现I点左拐到G于是G入栈。
加入I点向右,或不改变方向到G,则说明D,C,G会形成凸壳——此时将I弹出栈
观察向左拐还是向右拐可以用叉积。下文会提。
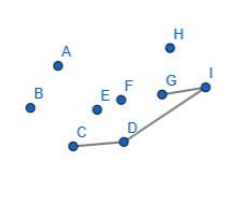
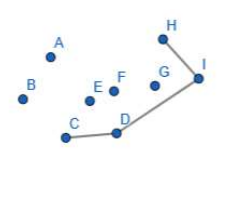
再考虑F。I-G-F不改变方向,于是弹G
D-I-G向左拐,不弹出
F入栈
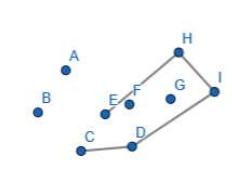
H入栈
考虑E。I-H-E向左拐,E入栈
H-E-A向右拐,弹出E
I-H-A向左拐,不弹,A入栈
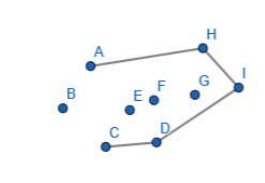
H-A-B向左拐,B入栈
求得凸包,结束。