[SIGMOD 2020]In-Memory Subgraph Matching An In-depth Study
In-Memory Subgraph Matching: An In-depth Study
一篇subgraph matching的survey
总结
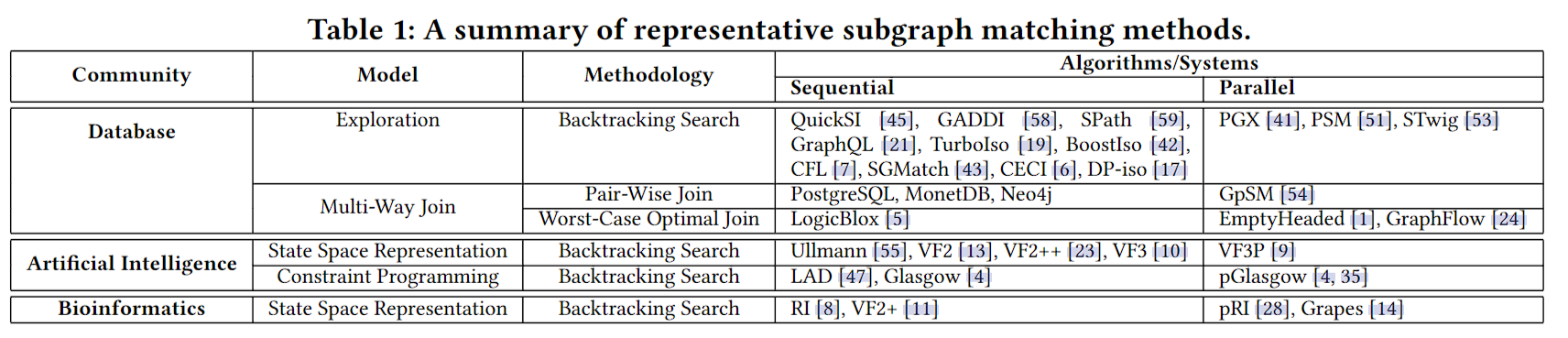
文章共分析了8中代表性的内存式子图匹配算法,在过滤、排序、扩展、优化四个方面做了对比。
定义
文中的重要符号表
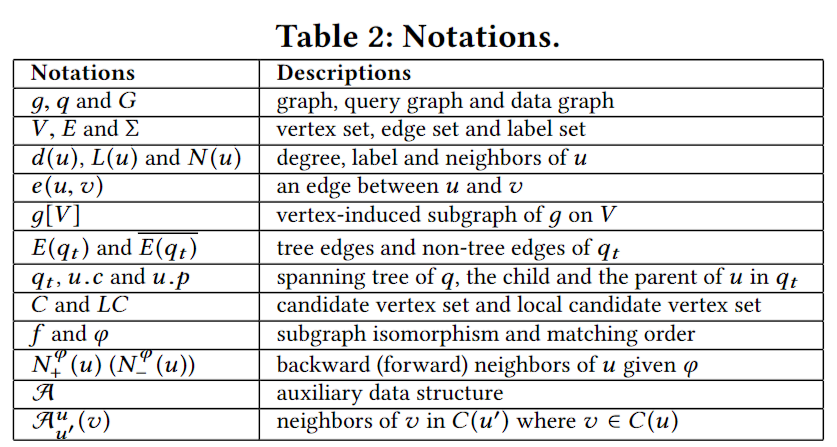
生成树的概念:生成树是一个连通图的最小连通子图
问题定义
子图同构问题是找一个单射函数,能把一张图的所有点和边映射到另一张图上。
子图匹配问题就是找到所有的子图同构。
这篇文章里的定义似乎有问题,根据他的定义,在一张图中删几条边可以算是子图,但实际上同构需要保证点和边都一一对应。
文章后面会统一将2-core内的点成为core点。说明候选集最小时,默认是候选集或者对应标签的点数/度数最小。
一般框架

第一行提取candidate,第二行确定order,第三行记录所有的点的映射,存在M里。如果当前M中的映射数量已经和order一样多了就代表已经找到了这些点的所有匹配,就可以输出了,否则就继续匹配。
第六行提取的u其实就是还没有M,且order里u点之前的所有点都有匹配了的点(order里下一个还没匹配的点)。
第七行的ComputeLC:
换句话说,在候选点集里挑出哪些已经匹配了的u的邻居点mapping后的点的邻居。说白了,邻居对应的点的邻居应该跟自己匹配。
取出这些lc后,用递归判断每个候选的点。
算法比较和分析
-
基本方法:
- 生成\(C(u)\)的方法通常是借助标签和度数(label and degree filtering, LDF):
\[C(u) = \{v \in V(G) | L(v) = L(u) \wedge d(v) \leq d(u)\} \]也就是标签相等,度数大于等于的点才有可能被匹配。
-
邻居标签频率过滤(neighbor label frequency filtering, NLF):对于查询图中的所有点\(u\),检测数据图中的所有点\(v\):
- 求出\(u\)的所有邻居标签集合\(L(N(u))={L(u')|u' \in N(u)}\)。
- 对于每个\(v\),检查对于\(L(N(u))\)中的每个标签\(l\):\(u\)的邻居中标签为\(l\)的点集\(N(u, l)\)和\(v\)的\(l\)标签的邻居\(N(v, l)\),满足后者比前者大,就继续判断下个label,否则就不是候选点。
关于完备候选集和的一个观察结果:
假设每个查询图q中的点u都生成了晚辈的候选集C(u),用\(S_{u'}\)表示C(u)中某个顶点v的邻居集合与u的邻居u'的C(u')的交集。如果(u, v)映射存在于一个匹配中,v就必须满足对于每个u'都有个不为空的\(S_{u'}\)。
说人话,我要是能和你配对,那我的邻居的候选点集里肯定有你的邻居。
该观察结果是CFL和CECI的理论基础。这个观察可以得到两个规则:
- 生成规则:u的候选点集是它的邻居的候选点集的邻居交集。
- 过滤规则:\(u\)的邻居的候选集和\(u\)的候选集的邻居交集非空,否则可以将该点可以从\(u\)的候选集删除。
此外,GraphQL中用到了第三个规则: - u的邻居的候选和u的候选的邻居的交集,每个邻居取它们各自交集中的一个点出来,能够保证不重复。
CFL,CECI和DP-iso使用1和2,而GraphQL用2和3
具体的算法实现过程

CFL的局部候选生成:根节点返回C(u)。如果u只有父节点是邻居,直接在A中取父节点的映射在C(u)中的邻居,否则对父节点的映射的邻居交集进行遍历检查过滤。
- CFL:
- 找出2-core的核心点,根据NLF生成初始候选集,选三个标签匹配/度数最小的点,再比较|C(u)|,选最小的点作为根节点构建BFS树
- 沿着BFS树,利用生成规则,不断取交集生成新的候选集,并利用非树边进行过滤。这一步的生成过程会记录下候选的邻居与父节点的候选之间的映射关系,从而生成辅助结构。沿着树再从下到上,继续使用非树边精炼候选集。
- 生成匹配顺序,策略是比较根到叶的所有路径的过滤效率(顺着这条路实现匹配的排列组合数量/非树边数量),效率最大的路径上的点优先添加。后面依次加入连接着已排序的点的最大效率序列。
- 使用精炼后的候选集和匹配顺序进行回溯搜索枚举匹配(算法1)。此外还会使用辅助结构直接获取局部候选集,因为已经构建了候选的邻居同父节点的候选之间的映射关系,可以根据父节点的映射的邻居获得局部候选(需要度和标签检查以及剪枝检查,保证符合已有的连通关系)。

CECI和DP-iso的局部候选生成:根节点返回C(u)。如果u只有一个已映射邻居u.p,直接从A中取u.p的映射在C(u)中的邻居,否则利用A计算每个已映射邻居的映射在C(u)中的邻居的交集。
-
CECI:
CECI的辅助结构是图结构,保留了查询图中的所有边。对每条边,辅助结构会记录两点候选集之间的邻接关系。- 建树、生成和过滤过程和CFL相同。BFS树生成过程中生成辅助结构。
- 直接使用BFS顺序作为匹配顺序。
- 利用辅助结构的候选关系进行交集运算,获取局部候选,再递归搜索扩展匹配(除了局部候选不同,其他和CFL相同)。
-
DP-iso:
动态排序,使用Failing set剪枝优化,候选生成使用多轮反复过滤。其他步骤同CECI。- 动态排序:预处理阶段生成一个静态序列(如用BFS顺序),搜索过程中计算所有可扩展点的局部候选集,选择最小的,如果存在候选集一样大则BFS顺序。
- Failing set剪枝:搜索过程中如果扩展某个点出现失败,且不是这个点本身造成的(也就是后面的匹配分支出现问题),就进行记录,下次碰到相同的必然失败的分支就直接剪枝。
- 多轮过滤:为了动态排序,进行多轮过滤,保证候选集的质量。

QuickSI和RI的局部候选生成:根节点返回C(u)。其他点u,遍历u的父节点在数据图中的映射的邻居集,对每个邻居w判断是否满足和u的标签和度的条件,以及能否和已经映射的u的其他邻居连通。
-
QuickSI:
- 使用基础的标签和度生成候选集
- 使用查询图边的频率生成匹配顺序
- 使用最基本的回溯搜索框架匹配扩展
- 通过检查数据图的边获取局部候选
整体来说,QuickSI非常简单轻量,所以搜索效率较差。
-
RI:
和QuickSI相比:- RI只在搜索时按需生成局部候选
- 排序标准基于顶点邻居关系
开始生成排序时,选择查询图中度最大的点加入顺序。之后不断重复:未加入的点中选择和已加入的点的共同邻居最多的点,如果并列则选未加入序列的共同邻居最多的,如果还并列就选择未加入序列的邻居数最多的
可以说RI是重在精简预处理,匹配时再想办法的算法

GraphQL的局部候选生成:如果是根节点,返回C(u),否则对每个候选V,检查u已映射的邻居在数据图中的连通情况。
-
GraphQL:
- 候选集的生成分为局部过滤和全局优化。
- 根据查询图的候选集大小生成排序
- 基础的回溯搜索来实现枚举,利用遍历候选集获得局部候选。
局部过滤:查询图的点u和它的r跳构成子图 profile u。如果数据图中有个点v的profile包含profile u,则该点是候选点,加入\(C(u)\)中
全局优化:对于每一个\(v \in C(u)\),构建uv间的二部图,两侧分别是u和v的邻居,如果v的邻居v'在u的邻居u'的\(C(u')\)中,则加边(u', v')。建立完成后,检查u的所有邻居是否都能匹配上,如果不行就把v从\(C(u)\)中删去。全局优化的优化次数由用户指定。
局部候选的获取方式检查候选是否是该点的邻居的映射点的邻居。
-
VF2++:
- 候选按需生成
- 排序基于查询顶点在数据图中的频率(看标签),频率最小的(能用标签匹配上的最少的)作为根节点,建造BFS树。每次在当前层的没进序列的点中选择一个拥有最多序列内的邻居的点。打破并列的两个规则:1. 度更大, 2. 标签匹配频率更小
- 基础的回溯搜索来枚举
- 检查数据图边生成局部候选
-
Glasgow:
该算法把子图匹配问题建模为约束满足问题,查询图的顶点和边分别对应变量和约束。- 候选利用邻居度数进行过滤
- 搜索过程中动态选择度最小的未匹配的点
- 回溯枚举
- 会优先搜索度数大的候选映射。
分析
-
候选生成和过滤:
-
基本方法有标签过滤、度过滤、频率过滤。
-
GraphQL使用局部拓扑结构的过滤效果不同数据集效果不同。
-
CFL、CECI、DP的过滤方法效果近似,优于GraphQL。
-
CFL使用生成规则和过滤规则的组合方法。
-
CECI融合BFS树与非树边进行多阶段过滤。
-
DP进行多轮过滤可显著提升效果。
-
过滤方法很依赖标签集大小,标签少时GraphQL效果好。
-
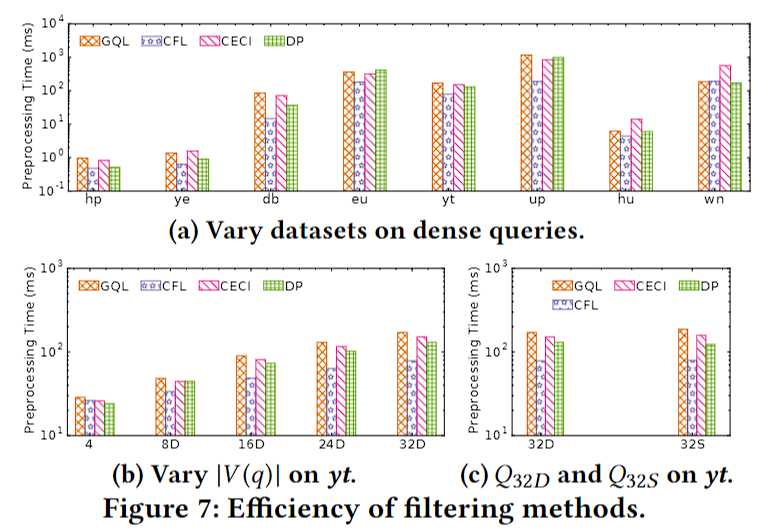
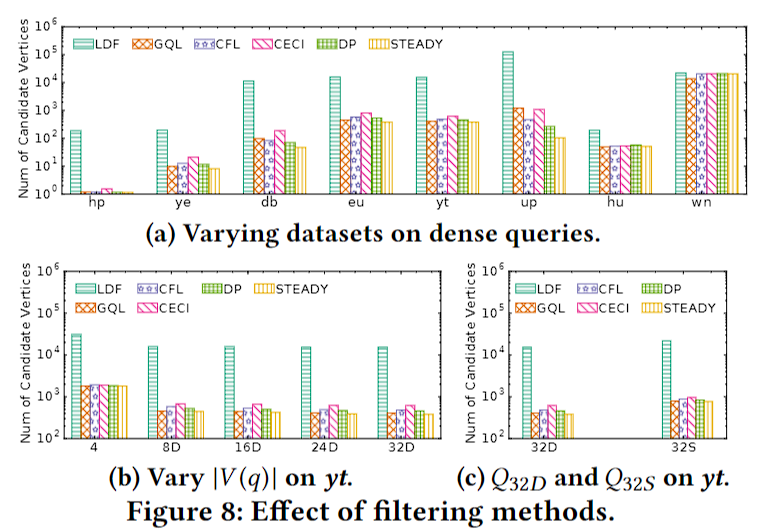
整体而言,CFL、CECI和DP的过滤方法优化效果相近。
-
时间和空间复杂度上CFL和DP较优于CECI。
-
-
局部候选生成:
-
QuickSI和RI直接访问原始图,复杂度与候选邻居相关。
-
GraphQL遍历完整候选集,复杂度与候选集大小线性相关。
-
CFL利用树结构,复杂度与候选交集相关。
-
CECI和DP利用集合交运算,复杂度与最小候选集相关。
-
维护候选集邻接辅助结构非常重要,可以显著减少复杂度。
-
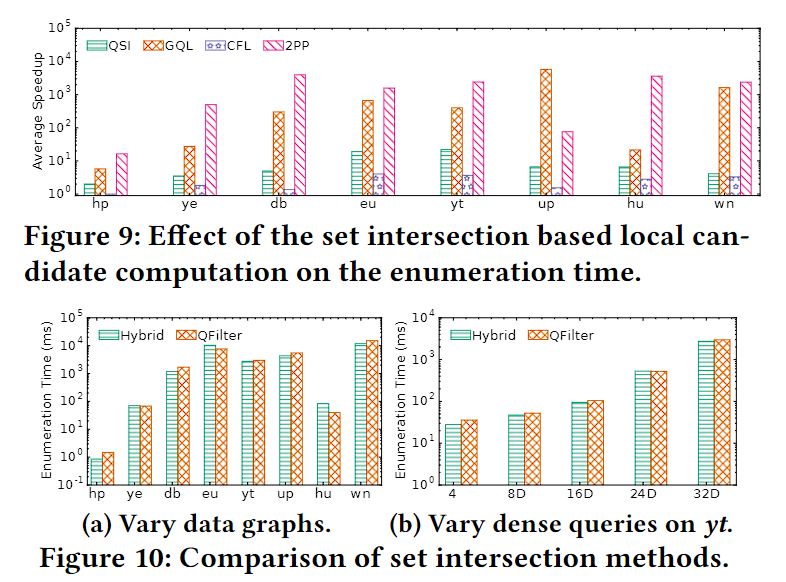
CECI和DP的集合交运算方法效率最高。
-
对超大图,交运算可以采用更优方法,如QFilter。
-
整体而言,CECI和DP的局部候选集生成算法优化效果最好。
-
实验
数据集
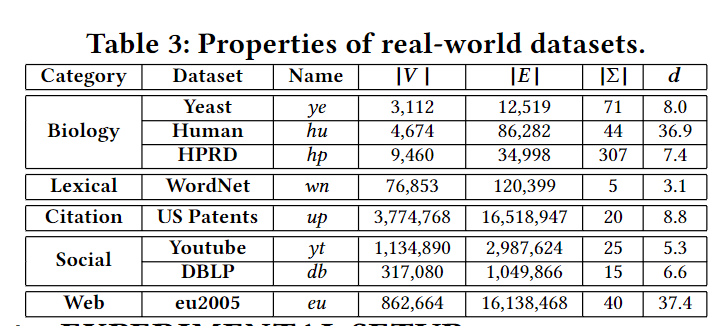
没标签的会随机选择标签集并分配给顶点。
每个数据集生成四个不同大小的数据图:点数为1M,4M,16M和64M;生成四个不同度数的数据图:8,12,16,20;生成四个标签数不同的数据图:8,12,16和20。
查询图是从数据图中采样出来的。对于每个数据集生成九组,每组包含点数相等的200个连通图。所有查询图的点数在4到32个之间。此外,还生成了四组稠密查询图和四组稀疏查询图。
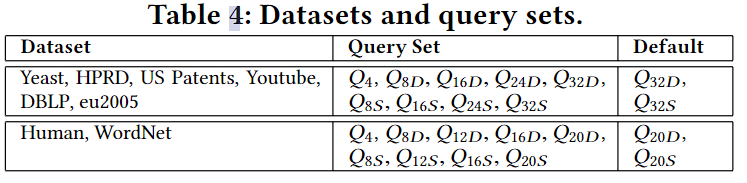
实验结果