平衡二叉查找树--splay
splay树,又称伸展树,是一种平衡二叉查找树,通过不断把每个节点旋转到根节点能够在O(logN)的时间内完成插入、查找以及删除的操作,并且能保持平衡不会退化成链
一、关于二叉查找树
首先,二叉查找树肯定是个二叉树(废话),每个节点的左子节点的值小于该节点的值小于右子节点的值。这个定义听起来十分耳熟 ,是的,堆就是一种二叉查找树
 这是卡比,卡比堆
这是卡比,卡比堆
一般二叉查找树的每个节点会带两种变量,一种是优先级,一种是该节点所代表的信息,以该节点的优先级建堆就可以得到一个二叉查找树
很显然二叉查找树找到一个节点所花费的时间与其深度成正比,最好情况下花费为O(log n),最坏情况下为O(n),即,树退化成了一条链
当花费为O(log n)时,树是一种类似完全二叉树的形态,这个时候我们称这棵树是平衡的,即这棵树是一个平衡查找二叉树(是的,这个名字就是如此的简单粗暴)
二、平衡树
如果一棵树的每一个节点的左子树和右子树的高度差最多为一,则称这个树是平衡的,一个合理的二叉搜索树即一个平衡查找二叉树的插入和查找时间可以缩短到O(log n)(这是显然的,因为当这棵树是平衡的时其深度会最小)
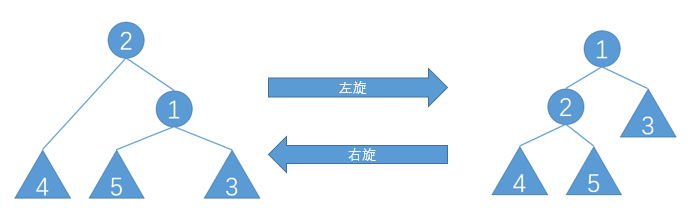
在插入和删除的过程中,二叉查找树可能会失衡,平衡树会通过“旋转”操作调整整棵二叉树的形态,其基本操作为左旋(zig)和右旋(zag),若要被旋转的点是其父节点的左子节点则进行右旋,反之左旋
为了使得这棵树的中序遍历不变,左旋内容如下:
一、使该节点的左子树成为该节点父节点的右子树
二、使该节点的父节点成为该节点的左子树
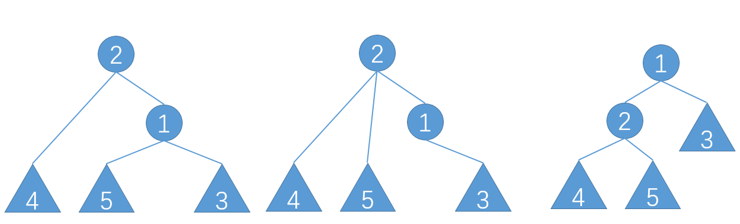
右旋同理
经过尝试,如果某个节点需要连续进行若干次(大于等于4次)的左旋或若干次右旋操作时,会有一种更优的旋转方法称为双旋
就比如下面这个例子,若我要把节点5旋转到根节点
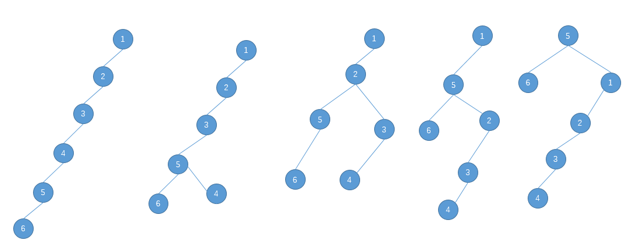
最终这棵树的深度是5
但如果每次旋转节点5之前我们先旋转其父节点,然后再旋转节点5,直到节点5成为根节点,最终会有不同的效果
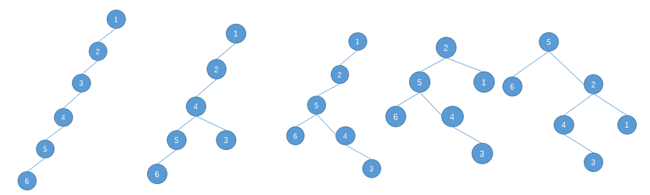
显然,第二种转法在转完后整棵树的深度比第一种转法整棵树的深度小一,根据前文提到的关于查找树的复杂度,第二种转法更优
这还只是五次右旋,如果连续旋转的次数更多,第二种转法与第一种的差距会越来越大,第二种转法就是所谓的双旋
看下代码
void rotate(int x)
{
int fa=f[x],grand=f[fa],son1=get(x),son2=(son1+1)%2;//f存储某节点的父节点编号 get是查找该节点是其父节点的左子节点还是右子节点 0为左 1为右
sons[fa][son1]=sons[x][son2];//将子节点挂到父节点上去
f[sons[fa][son1]]=fa;
sons[x][son2]=fa;
f[fa]=x;//更新关系
f[x]=grand;
if(grand)
{
sons[grand][sons[grand][1]==fa]=x;//如果有祖父节点要令祖父节点成为该节点的父节点
}
//upd(fa);
//upd(x);
}
void splay(int x)
{
for(int fa;fa=f[x];rotate(x))//旋转直到x成为根节点
{
if(f[fa]) rotate((get(x)==get(fa))?fa:x);//双旋
}
root=x;//更新根节点
}
在保持中序遍历不变的前提下,使用若干次“旋转”操作可以使这棵树平衡
三、伸展树splay
splay实际上不算是严格的平衡树,事实上很多情况下它都不咋平衡,但是却能够在均摊O(logn)时间内完成插入,查找和删除操作,并且不至于退化为链
至于为什么能够均摊O(logn)的时间……这个算起来挺复杂的,这里就不赘述了因为我不会
splay的主要功能包括高效的插入、删除、查询、修改
先来看看插入如何实现
1、如果根节点为空,非常显然的事,这根本不需要插入,因为原本就没有树!直接让该节点成为根节点
代码如下
if(!root)//如果根节点为空
{
whole_size++;//整棵树的大小增加一
sons[whole_size][0]=sons[whole_size][1]=f[whole_size]=0;//默认有一定BST基础,所以这是一个很显然的初始化
root=whole_size;//初始化根节点
sub_size[whole_size]=cnt[whole_size]++;//sub_size 指的是以某节点为根节点的子树的大小 cnt存储的是某数被插入的次数
val[whole_size]=x;//该节点的数值
return ;
}
2、如果根节点不为空,根据二叉查找树的性质,从根节点起,若该数小于当前节点往左子树走,反之则往右子树,如果等于,则当前节点的cnt++
如果走到了一个为空的子树,则直接添加该节点
然后,将新添加的节点或刚累加了cnt的节点旋转至根节点
例如,现在在已有的树上插入一个3一个6
第一次

第二次
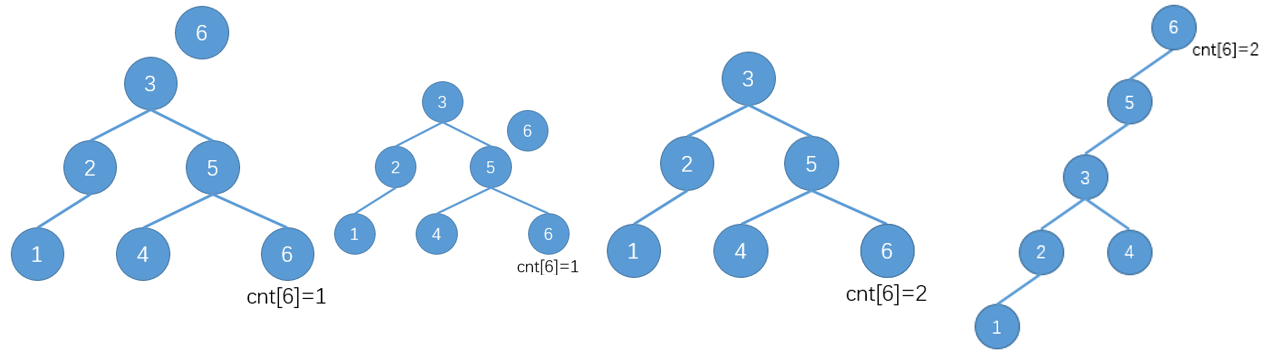
看看代码
void insert(int x)
{
if(!root)//如果根节点为空
{
whole_size++;//整棵树的大小增加一
sons[whole_size][0]=sons[whole_size][1]=f[whole_size]=0;//默认有一定BST基础,所以这是一个很显然的初始化
root=whole_size;//初始化根节点
sub_size[whole_size]=cnt[whole_size]++;//sub_size 指的是以某节点为根节点的子树的大小,以后会用到的 cnt存储的是某数被插入的次数
val[whole_size]=x;//该节点的数值
return ;
}
int now=root,fa=0;//从根节点开始走 now表示当前位置 fa表示父亲节点
while(1)
{
if(x==val[now])//如果找到了数值相等的点,则cnt[now]++
{
cnt[now]++;
upd(now);//以后会用到的
upd(fa);
splay(now);//转到根节点
break;
}
fa=now;
now=sons[now][val[now]<x];//若val[now]<x则会返回1,前往右子树,反之亦然
if(!now)//如果走到了空子树
{
whole_size++;//整个splay大小+1
sons[whole_size][0]=sons[whole_size][1]=0;//初始化左右儿子
f[whole_size]=fa;//设置父亲节点
sub_size[whole_size]=cnt[whole_size]=1;//初始化本子树大小
sons[fa][val[fa]<x]=whole_size;//与父节点连接
val[whole_size]=x;//设置该点数值
upd(fa);
splay(whole_size);//转到根节点
break;
}
}
}