2023.8.3模拟
T1 跑路
Description
定义“好矩阵”为存在一条从左上角到右下角曼哈顿距离最短的路径满足只经过\(0\)的\(01\)矩阵,可以进行一次操作对任意子矩阵取反,求最小的操作次数使给定的、大小为\(n \times m\)的矩阵变成“好矩阵”。
\(n, m \leq 1000\)
Solution
画两下不难发现一次操作可以使路径上连续的一段\(1\)变为\(0\),接下来就是板子般的\(dp\)了。
Code
#include<bits/stdc++.h>
using namespace std;
const int MaxN = 1010, INF = 1e9;
int n, m, a[MaxN][MaxN], f[MaxN][MaxN];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
scanf("%d", &a[i][j]), f[i][j] = INF;
f[1][1] = (a[1][1] == 0)?1:2;
for (int i = 2; i <= n; ++i)
f[i][1] = f[i-1][1]+((a[i][1] != a[i-1][1])?1:0);
for (int i = 2; i <= m; ++i)
f[1][i] = f[1][i-1]+((a[1][i] != a[1][i-1])?1:0);
for (int i = 2; i <= n; ++i)
for (int j = 2; j <= m; ++j) {
f[i][j] = min(f[i][j], f[i][j-1]+((a[i][j] != a[i][j-1])?1:0));
f[i][j] = min(f[i][j], f[i-1][j]+((a[i][j] != a[i-1][j])?1:0));
}
printf("%d", f[n][m]/2);
return 0;
}
T2 清扫([AGC010C]Cleaning)
link:https://atcoder.jp/contests/agc010/tasks/agc010_c
Description
给出一颗大小为\(n\)的树,树上每个点有权值\(a_{1 \sim n}\),每次可以选择两个叶子节点,使它们之间路径上的所有点权值\(-1\),问是否能使所有点的权值为零。
\(2 \leq n \leq 10^5, 0 \leq a_i \leq 10^9\)
Solution
观察到叶子节点的操作次数\(=\)叶子节点的权值,再通过这条性质推导非叶子节点的情况,发现情况无非两种:
- 叶子节点和同一子树内的点相连。
- 叶子节点与不同子树的点相连。
也可以参考这张图:
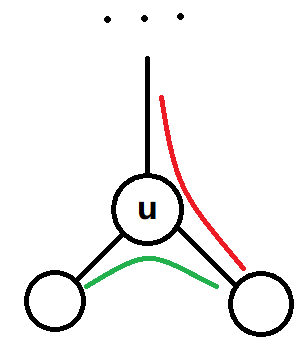
发现情况1对点\(u\)的贡献需要除以\(2\)(绿色路径),而情况二不用(红色路径),又因点\(u\)的权值是确定的,所以便可以计算出点\(u\)对上方节点的贡献。
实现代码是还需要注意下方节点最大值与下方节点总和对点\(u\)的总贡献范围限制, 因为如果有节点贡献大于总和的\(\frac{1}{2}\),就必须有部分红色路径。
选择一个非叶子节点为根\(dfs\)即可,时间复杂度\(O(n)\)
Code
#include<bits/stdc++.h>
using namespace std;
const int MaxN = 100010;
struct Blck
{int to, next;}e[MaxN<<1];
int ecnt, head[MaxN<<1];
void add(int u, int v)
{e[++ecnt].to = v; e[ecnt].next = head[u]; head[u] = ecnt;}
int deg[MaxN];
long long a[MaxN], f[MaxN];
bool flag;
void dfs(int x, int pre) {
if (deg[x] == 1) {f[x] = a[x]; return ;}
long long mx = 0;
int y;
for (int i = head[x]; i; i = e[i].next) {
y = e[i].to;
if (y != pre) dfs(y, x), f[x] += f[y], mx = max(mx, f[y]);
if (flag) return ;
}
long long res;
if (mx > f[x]-mx) res = f[x]-mx;
else res = f[x]>>1;
if (f[x]-res > a[x] || f[x] < a[x]) {
printf("NO\n");
flag = 1;
return ;
} f[x] -= 2ll*(f[x]-a[x]);
}
int t, n;
int main() {
int u, v, root;
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i < n; ++i) {
scanf("%d%d", &u, &v);
++deg[u]; ++deg[v];
add(u, v); add(v, u);
}
if (n == 1) {
printf("%s\n", (a[1] == 0)?"YES":"NO");
return 0;
}
if (n == 2) {
printf("%s\n", (a[1] == a[2])?"YES":"NO");
return 0;
}
for (int i = 1; i <= n; ++i) if (deg[i] != 1) root = i;
dfs(root, -1);
if (!flag) {
if (f[root]) printf("NO\n");
else printf("YES\n");
}
return 0;
}
T3 定向([ARC092F] Two Faced Edges)
link:https://atcoder.jp/contests/arc092/tasks/arc092_f
Description
有一个\(N\)个点\(M\)条边的有向图。保证图中不存在重边和自环。试判断将每条边反向,其他边不变的情况下,图中强连通分量的数量是否改变。若改变,输出 diff,否则输出 same。
\(1 \leq N \leq 10^3, 1 \leq M \leq 2 \times 10^5\)
Solution
改变一条边\(u \rightarrow v\)的方向会使强连通分量增加、减少或不变,对这三种情况讨论:
- 当强连通分量增加时,说明\(u, v\)在同一强连通分量中,且图中不存在一条从\(u\)到\(v\)的路径(不包含边\(u \rightarrow v\))。
- 当强连通分量减少时,说明\(u, v\)不在同一强连通分量中,且图中存在一条从\(u\)到\(v\)的路径(不包含边\(u \rightarrow v\))。
- 当强连通分量不变时,说明\(u, v\)不在同一强连通分量中,且图中不存在一条从\(u\)到\(v\)的路径(不包含边\(u \rightarrow v\));或\(u, v\)在同一强连通分量中,且图中存在一条从\(u\)到\(v\)的路径(不包含边\(u \rightarrow v\))。
记\(f(u, v)\)表示是否在同一强连通分量中,\(g(u, v)\)表示且图中是否存在一条从\(u\)到\(v\)的路径(不包含边\(u \rightarrow v\)),不难发现当\(f(u, v) \oplus g(u, v) = 1\)时,边\(u \rightarrow v\)的答案为same,否则答案为diff。
对于\(f(u, v)\),一次tarjan即可预处理,接下来考虑如何计算\(g(u, v)\)
发现可以通过翻转搜索时的边表顺序来确定是否存在边\(u \rightarrow v\),因此通过两次dfs,可以一次性预处理出所有的\(g(u, \_)\)
时间复杂度方面,每次dfs复杂度\(O(m)\),共搜索\(n\)次,总共\(O(n, m)\)
(听说还有一种bitset做法\(O(\frac{n^3}{w})\),鸽了)
Code
#include<bits/stdc++.h>
using namespace std;
const int MaxN = 1010, MaxM = 200010;
bool vis[MaxN];
int dfn[MaxN], low[MaxN], st[MaxN], c[MaxN], num, top, cnt;
vector<int> scc[MaxN], G[MaxN];
void tarjan(int x) {
dfn[x] = low[x] = ++num;
st[++top] = x; vis[x] = 1;
for (int i = 0; i < G[x].size(); ++i) {
int v = G[x][i];
if (!dfn[v]) {
tarjan(v);
low[x] = min(low[x], low[v]);
} else if(vis[v])
low[x] = min(low[x], dfn[v]);
}
if (dfn[x] == low[x]) {
++cnt;
int y;
do {
y = st[top--];
vis[y] = 0;
c[y] = cnt;
scc[cnt].push_back(y);
} while (x != y);
}
}
int de1[MaxN], de2[MaxN], vis1[MaxN], vis2[MaxN];
void dfs(int x, int dep, int pre) {
de1[x] = dep; vis1[x] = 1;
for (int i = 0; i < G[x].size(); ++i) {
int y = G[x][i];
if (y != pre && !vis1[y])
dfs(y, dep+1, x);
}
}
void dfs2(int x, int dep, int pre) {
de2[x] = dep; vis2[x] = 1;
for (int i = G[x].size()-1; ~i; --i) {
int y = G[x][i];
if (y != pre && !vis2[y])
dfs2(y, dep+1, x);
}
}
int n, m, u[MaxM], v[MaxM], f[MaxN][MaxN], g[MaxN][MaxN];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; ++i) {
scanf("%d%d", &u[i], &v[i]);
G[u[i]].push_back(v[i]);
}
for (int i = 1; i <= n; ++i) if (!dfn[i]) tarjan(i);
int sl;
for (int i = 1; i <= cnt; ++i) {
sl = scc[i].size();
for (int j = 0; j < sl-1; ++j)
for (int k = j+1; k < sl; ++k)
f[scc[i][j]][scc[i][k]] = f[scc[i][k]][scc[i][j]] = 1;
}
for (int i = 1; i <= n; ++i) {
memset(vis1, 0, sizeof(vis1));
memset(vis2, 0, sizeof(vis2));
dfs(i, 0, -1), dfs2(i, 0, -1);
for (int j = 1; j <= n; ++j)
if (j != i) g[i][j] = !(de1[j] == 1 && de2[j] == 1);
}
for (int i = 1; i <= m; ++i)
printf("%s\n", (g[u[i]][v[i]]^f[u[i]][v[i]])?"diff":"same");
return 0;
}
T4 染色([ARC089F]ColoringBalls)
link:https://atcoder.jp/contests/arc089/tasks/arc089_f
Description
有\(N\)个白色的小球排成一排,有一个长为\(K\)的字符串\(S\)。接下来进行\(K\)次操作。
第\(i\)个操作,选择一段连续的小球(可以为空),若\(S\)中第\(i\)个字符是\(r\),则将这些球染成红色;若是\(b\),则将它们染成蓝色。由于染料的特性,不能直接用蓝色来染白色。
求在进行完所有操作后,所有小球的颜色序列可以有多少种。
对\(10^9+7\)取模。
\(1 \leq N,K \leq 70, |s|=K\)
Solution
如Kubic老师所言:“看到这种形式题目的一般都先转化为考虑对于一种结果,是否存在方案满足要求”,判断后我们在考虑如何计数。
判断是否存在方案满足要求
发现段的长短并不影响方案,因此一段段考虑结果。
白色球是初始状态,因此考虑将白球段作为分割点,那么剩下两种段,一种纯红色,一种红蓝混合。
显然红色段只需要一个\(r\)即可。
对于蓝色段,创造出第一段蓝色需要一个“\(\{r,b\}\)”,然后每一个字符都可以使蓝色段数\(+1\)(在蓝色段中插入红色或在初始红色段上添加蓝色)。
记第\(i\)个\(\{r, b\}\)后未选择的字符数有\(t_i\)个,还需\(s_i\)个字符满足。
贪心地每次取最靠左的字符,那么充要条件便是
显然\(s\)降序排列时最有可能满足条件。
枚举有\(a\)个纯红色段,\(c\)个混合段,判断是否有方案后,接下来就可以计数了。
DP计数
先鸽一小下
Code
#include<bits/stdc++.h>
using namespace std;
const int MaxN = 80, MaxC = 210;
const long long mod = 1e9+7;
long long C[MaxC][MaxC];
void getC() {
for (int i = 0; i <= 200; ++i) {
C[i][0] = 1;
for (int j = 1; j <= i; ++j)
C[i][j] = (C[i-1][j-1]+C[i-1][j])%mod;
}
}
char str[MaxN];
bool vis[MaxN];
int st[MaxN], n, k;
bool check(int c, int a) { //判断状态是否合法(顺便处理所需杂色段rb位置)
int tot = 0, bpos; st[0] = 0;
for (int i = 1; i <= k; ++i) if (str[i] == 'r') {
if (tot < c) { //加入杂色段
++tot;
bpos = -1;
for (int j = i+1; j <= k; ++j)
if (str[j] == 'b' && !vis[j]) {bpos = j; break ;}
if (!(~bpos)) return false;
vis[i] = vis[bpos] = true;
st[++st[0]] = bpos;
} else {
if (tot < c+a) ++tot, vis[i] = true; //加入纯色段
else break ;
}
}
if (tot == a+c) return true ;
else return false;
}
long long dp[MaxN][50][50], sum[MaxN], w[MaxN];
long long solve (int c, int a) {
if (!c && !a) return 1;
memset(vis, 0, sizeof(vis));
if(!check(c, a)) return 0;
memset(dp, 0, sizeof(dp));
for (int i = k; i; --i) sum[i] = sum[i+1]+(!vis[i]);
for (int i = 1; i <= c; ++i) w[i] = sum[st[c-i+1]]+i;
long long s; dp[0][0][0] = 1;
for (int i = 0; i < c; ++i) for (int j = 0; j <= w[i] && (j+a)*2-1 <= n; ++j) //解决问题,还是只会仰仗dp
for (int p = 1, s = dp[i][j][0]; j+p <= w[i+1] && (j+p+a)*2-1 <= n; ++p) {
for (int l = 1; i+l <= c && j+p*l <= w[i+l] && (j+p*l+a)*2-1 <= n; ++l)
dp[i+l][j+p*l][p] = (dp[i+l][j+p*l][p]+1ll*s*C[i+l][l]%mod)%mod;
s = (s+dp[i][j][p])%mod;
}
int tmp1, tmp2; long long ans = 0;
for (int i = 0; i <= w[c] && (i+a)*2-1 <= n; ++i) {
s = 0, tmp1 = (i+a)*2-1, tmp2 = c*2+2;
for (int j = 0; j <= i; ++j) s = (s+dp[c][i][j])%mod;
ans = (ans+1ll*s*C[n+tmp2-1][tmp1+tmp2-1]%mod)%mod;
} ans = 1ll*ans*C[a+c][c]%mod; return ans;
}
int main() {
long long ans = 0;
getC();
scanf("%d%d%s", &n, &k, str+1);
for (int c = 0; 2*c <= k; ++c)
for (int a = 0; 2*c+a <= k; ++a)
ans = (ans+solve(c, a))%mod;
printf("%lld", ans);
return 0;
}
sumary
考场上只切了一道……t2的正解在考场上大概想出来了,为求保险还是没有去写。
写到t3时脑子已经不在了,直接暴力tarjan骗40分
还是有很多问题的吧:
- 码力还是太差了……
- 考场上有正解还是要冲一冲(万一冲对了呢
- 要充分转化题目使其变为好下手的
- 有时候要考虑拆分题目,一个个条件解决