23.8.7 NOIP模拟赛
纯菜,100+90+0+40。
T1

不会正解,发现每个位置 \(i\) 可以转到的位置 可以表示成 \(l,l+2,l+4...r\)。那么这些位置是奇偶的连续一段,相当于单点向区间连边,直接建两棵线段树优化建图即可,复杂度 \(O(n\log n)\)
code
#include<bits/stdc++.h>
#define psb push_back
typedef long long LL;
using namespace std;
const int N=1e5+5,M=2e6+5; vector<pair<int,int>> vt[M];
int n,k,m,S,gn,bd[N];
bool sp[N];
struct subT{
int bid[N<<2],fd[N];
void build(int p,int L,int R){
if(L==R) { fd[L]=bid[p]=++gn; return ;}
bid[p]=++gn; int mid=(L+R)/2;
build(p<<1,L,mid); build(p<<1|1,mid+1,R);
vt[bid[p]].psb({bid[p<<1],0}); vt[bid[p]].psb({bid[p<<1|1],0});
}
void Adde(int p,int L,int R,int lt,int rt,int s){
if(L>rt || R<lt || lt>rt) return ;
if(L>=lt && R<=rt) { vt[s].psb({bid[p],0}); return; }
int mid=(L+R)/2;
Adde(p<<1,L,mid,lt,rt,s); Adde(p<<1|1,mid+1,R,lt,rt,s);
}
} T[2];
int f[M];
void BFS(){
deque<int> q; q.psb(bd[S]);
memset(f,-1,sizeof(f)); f[bd[S]]=0;
while(!q.empty()){
int u=q.front(); q.pop_front();
for(auto i:vt[u]){
int v=i.first,w=i.second;
if(f[v]!=-1) continue;
f[v]=f[u]+w;
if(w==0) q.push_front(v);
else q.psb(v);
}
}
}
int main(){
scanf("%d%d%d%d",&n,&k,&m,&S);
for(int i=1,x;i<=m;i++){ scanf("%d",&x); sp[x]=1;}
T[0].build(1,1,n); T[1].build(1,1,n);
for(int i=1;i<=n;i++){
bd[i]=T[i%2].fd[i];
if(sp[i]) continue;
int p=++gn; vt[bd[i]].psb({p,1});
int lt=(i>=k)?i-(k-1):k-i+1;
int rt=(i<=n-k+1)?i+(k-1):n-k+(n-i+1);
T[(i%2) ^ (k%2==0)].Adde(1,1,n,lt,rt,p);
}
BFS();
for(int i=1;i<=n;i++){
if(sp[i]) f[bd[i]]=-1;
printf("%d ",f[bd[i]]);
}
return 0;
}
T2
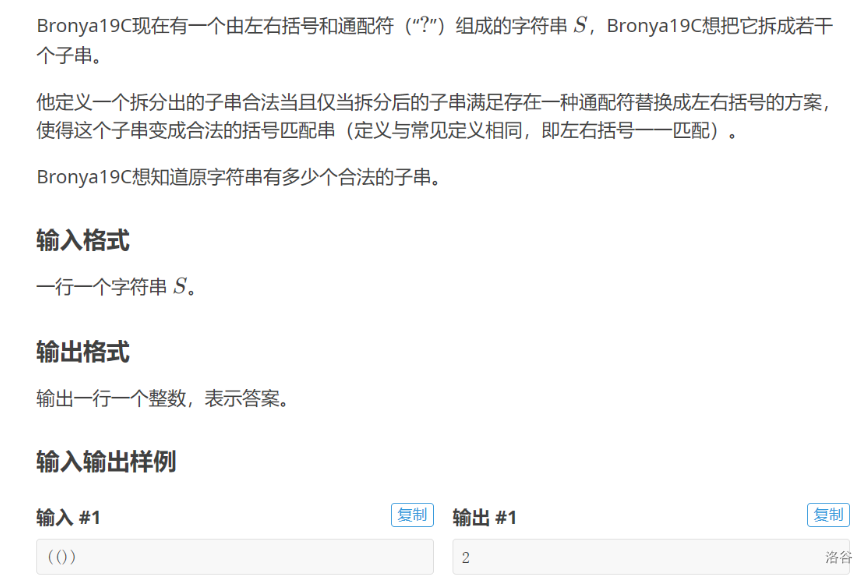
笔者很菜。赛时没有 AC。
关于括号序列我们有一个性质:
对于子串 \(S_{l..r}\) ,我们把 \("("\) 看作 \(1\),把 \(")"\) 看作 \(-1\)。
他是匹配括号串的充要条件是:这个子串的前缀和都 \(\ge 0\) 且整个的和为 \(0\) 。
我们进一步转化这个充要条件:
- 长度为偶数
- 把 \()\) 看作 \(-1\),其他看作 \(1\), 前缀和大于等于 \(0\)。
- 把 \((\) 看作 \(-1\),其他看作 \(1\),后缀和大于等于 \(0\)。
那么我们对于整个序列求一个前缀和 \(a\) 和后缀和 \(b\)。
对于合法区间 \([l,r]\) 他的充要条件是:
标算 \(O(n\log n)\) ,蒟蒻不会标算的二维数点,写了一个 \(CDQ\) 分治 \(O(n \log^2 n)\) 直接把这个 \(\min\) 拆成左边和右边的贡献,可以变成一个二维数点。见代码
code
#include<bits/stdc++.h>
typedef long long LL;
using namespace std;
const int N=1e6+5;
char ch[N];
int s1[N],s2[N],n;
struct date{
int a,b,id;
} q1[N],q2[N];
bool cmp(date x,date y){
return x.b>y.b;
}
struct Bit{
int fd[2*N];
inline void Addx(int x,int w){
x+=n+1;
for(int i=x;i<=2*n+2;i+=i & -i)
fd[i]+=w;
}
inline int Ask(int x){
x+=n+1; int y=0;
for(int i=x;i;i-=i & -i)
y+=fd[i];
return y;
}
inline void clr(int x){
x+=n+1;
for(int i=x;i<=2*n+2;i+=i & -i)
fd[i]=0;
}
} T[2];
LL ans=0;
void CDQ(int L,int R){
if(L==R) return ;
int mid=(L+R)/2;
int mn1=1e9,mn2=1e9,t1=0,t2=0;
for(int i=mid+1;i<=R;i++){
mn1=min(mn1,s1[i]); mn2=min(mn2,s2[i]);
if(mn2>=s2[i+1]) q1[++t1]=(date){mn1,s2[i+1],i};
}
mn1=1e9,mn2=1e9;
for(int i=mid;i>=L;i--){
mn1=min(mn1,s1[i]); mn2=min(mn2,s2[i]);
if(mn1>=s1[i-1]) q2[++t2]=(date){s1[i-1],mn2,i};
}
sort(q1+1,q1+t1+1,cmp); sort(q2+1,q2+t2+1,cmp);
for(int i=1,j=1;i<=t1;i++){
while(j<=t2 && q2[j].b>=q1[i].b) T[q2[j].id%2].Addx(q2[j].a,1) ,j++;
ans+= T[1-q1[i].id%2].Ask(q1[i].a);
}
for(int i=1;i<=t2;i++) T[q2[i].id%2].clr(q2[i].a);
CDQ(L,mid); CDQ(mid+1,R);
}
int main(){
scanf("%s",ch+1); n=strlen(ch+1);
for(int i=1;i<=n;i++) s1[i]=s1[i-1]+((ch[i]==')')?-1:1);
for(int i=n;i>=1;i--) s2[i]=s2[i+1]+((ch[i]=='(')?-1:1);
CDQ(1,n);
printf("%lld",ans);
return 0;
}
T3
link
赛时认为比 \(T4\) 难,没写爆 \(0\)。
看看回文串的性质,如果我们把 \(G\) 在串中的位置两两匹配,显然 \(H\) 也是匹配的。
那么我们把 \(G\) 的位置排序,贡献是