递归/搜索

RonChen / 2023-08-06 / 原文

递归

递归（Recursion）：函数在运行时调用自己

编写一个递归函数

这个递归函数的功能是什么，怎样调用这个函数，即设计好递归函数的返回值和参数列表
什么时候应该结束这个递归，它的边界条件（出口）是什么
在非边界情况时，怎样进行状态的转换

计算阶乘（factorial）

\[n! = \begin{cases} 1 & n=0 \\ n*(n-1)! & n>0 \end{cases} \]

int factorial(int n) {
	if (n == 0) return 1;
	return n * factorial(n - 1);
}
int ans = factorial(10); // 调用递归函数

计算最大公约数（辗转相除法）

gcd(12, 32) -> gcd(12, 8) -> gcd(8, 4) -> gcd(4, 0)

\[gcd(a,b) = \begin{cases} a & b = 0 \\ gcd(b, a\%b) & b \ne 0 \end{cases} \]

int gcd(int x, int y) {
	return y == 0 ? x : gcd(y, x % y);
}
int ans = gcd(12, 32);

例：P1028 [NOIP2001 普及组] 数的计算

比如说，数列中最开始只有一个元素8，在末尾加入一个新元素，列表就可以变成[8 4]、[8 3]、[8 2]、[8 1]，算上[8]一共有5种情况。如果之后还需要计算更长的数列的方案数，只需要按照上面这种方法，分别计算[4]、[3]、[2]、[1]按照这样的操作能有几种情况，然后累加统计即可。因为以4开头（3、2、1同理）的所有合法数列，都可以接续到8的后面
原本是要解决n=8的问题，现在分解成了4个规模更小（n=4,3,2,1）但本质上一样的子问题；如果要解决n=4的问题，基于同样的思想还可以分解成两个规模更小的（n=2,1）但本质上一样的子问题；当需要解决n=2的问题时，可以分解成n=1的问题（只有n=1的情况了）；直到n=1时，没法继续分解，此时可以直接返回只有唯一一种数列，即[1]。然后返回上一层（n=2）接收到所有小规模问题的答案，合并统计处理获得这个规模下的答案，再继续返回上一层（n=4），…… 直到求得问题的解

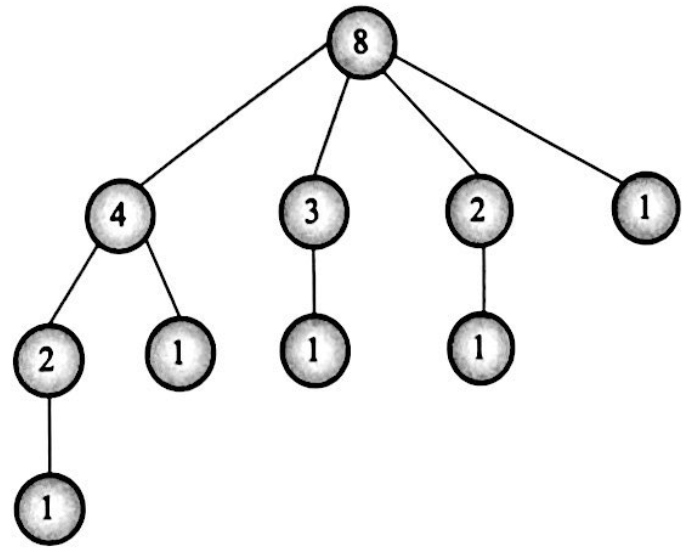
于是可以写出这样的程序：

#include <cstdio>
int solve(int n) {
    if (n == 1) return 1;
    int ret = 1;
    for (int i = 1; i <= n / 2; i++) ret += solve(i);
    return ret;
}
int main()
{
    int n;
    scanf("%d", &n);
    printf("%d\n", solve(n));
    return 0;
}

这个程序正确性上并没有问题，但是不能AC，运行效率低导致程序超时。这是因为做了很多无用功，比如 solve(2) 可能由 solve(4) 调用，也有可能被 solve(8) 调用，但是 solve(2) 本身的结果是固定不变的，在这里却重复执行了多次造成浪费
为了解决这个问题，可以定义一个数组 f，其每一项 f[i] 表示当问题规模为 i 时的结果。首先将数组全部初始化为 -1，表示 f[i] 还没有被计算过。依然使用同样的方法去求解，只是如果发现是已经计算过的问题，就直接返回 f[i] 而不必进行接下来的计算了，否则还是按照刚才的递归方式计算，然后将结果存入数组中以便之后再次调用。改进后的代码如下：

#include <cstdio>
const int MAXN = 1005;
int f[MAXN];
int solve(int n) {
    int ret = 1;
    if (f[n] != -1) return f[n];
    for (int i = 1; i <= n / 2; i++) ret += solve(i);
    return f[n] = ret;
}
int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) f[i] = -1;
    printf("%d\n", solve(n));
    return 0;
}

这样，每个数字最多只计算一次，因为一旦计算完成就会被存下来，便于日后使用。这样的思想称为“记忆化搜索”

深度优先搜索（DFS）

例：P1605 迷宫

存储迷宫
二维数组 b[x][y] 存储迷宫信息，兼职判重
dx[] dy[] 数组存方向偏移量
深搜与回溯
从起点开始，往四个方向尝试，能走就打上标记，锁定现场，然后走过去；到达目的地则更新答案；走投无路则返回，返回后要去除标记，恢复现场；继续尝试，直到尝遍所有可能，最终从入口退出。
深搜实际上对应一棵DFS树

#include <cstdio>
int n, m, t, ans;
int sx, sy, fx, fy;
int b[10][10];
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
void dfs(int x, int y) {
    if (x == fx && y == fy) {
        ++ans;
        return;
    }
    for (int i = 0; i < 4; ++i) {
        int xx = x + dx[i];
        int yy = y + dy[i];
        if (xx >= 1 && xx <= n && yy >= 1 && yy <= m && b[xx][yy] == 0) {
            b[xx][yy] = 1; // (xx,yy)被走过
            dfs(xx, yy);
            b[xx][yy] = 0; // 复原
        }
    }
}
int main()
{
    scanf("%d%d%d%d%d%d%d", &n, &m, &t, &sx, &sy, &fx, &fy);
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j) 
            b[i][j] = 0;
    for (int i = 0; i < t; ++i) {
        int x, y;
        scanf("%d%d", &x, &y);
        b[x][y] = 2;
    }
    b[sx][sy] = 1;
    dfs(sx, sy);
    printf("%d\n", ans);
    return 0;
}

例：P1644 跳马问题

用 dx[] dy[] 数组存方向偏移量
DFS搜索方案
从起点开始，向右边的四个点尝试，能走就走过去，一直到走投无路返回；到达目的地则更新答案；一直尝试，直到穷尽所有可能
由于本题限制了跳转方向，每个点不会往回走，所以不需要判重
深搜会生成DFS树

#include <cstdio>
const int MAXN = 20;
int n, m, ans;
int dx[4] = {2, 1, -1, -2};
int dy[4] = {1, 2, 2, 1};
void dfs(int x, int y) {
    if (x == n && y == m) {
        ans++;
        return;
    }
    for (int i = 0; i < 4; i++) {
        int xx = x + dx[i], yy = y + dy[i];
        if (xx >= 0 && xx <= n && yy <= m) dfs(xx, yy);
    }
}
int main()
{
    scanf("%d%d", &n, &m);
    dfs(0, 0);
    printf("%d\n", ans);
    return 0;
}

例：P1219 [USACO1.5] 八皇后

存储数据
ans数组记录各行放的位置
c数组标记某一列是否放置了棋子
d1数组标记副对角线，用到的下标范围是行+列 2,3,4,...,2n
d2数组标记主对角线，用到的下标范围是行-列+n（因为下标不能是负数，统一加n做偏移） 1,2,3,...,2n-1
DFS搜索方案
2.1 从第1行开始放，然后尝试放第2~n行
2.2 对于某一行，依次枚举每一列，如果某一列能放下，则记住放置位置，宣布占领该位置的辐射区域，然后继续搜索下一行
2.3 如果某一行的每一列都不能放下，则退回前一行，恢复现场，尝试前一行的下一列
2.4 如果能放满n行，说明找到了一种合法方案，则方案数+1，打印方案，接着返回上一行，继续搜索其他的合法方案，直到搜完所有的可能方案
2.5 因为是逐行逐列搜的，先搜到的方案字典序一定更小

#include <cstdio>
const int MAXN = 30;
int n, cnt;
int ans[MAXN], c[MAXN], d1[MAXN], d2[MAXN];
void dfs(int i) {
    if (i > n) {
        cnt++;
        if (cnt <= 3) {
            for (int j = 1; j <= n; j++) printf("%d ", ans[j]);
            printf("\n");
        }
        return;
    }
    for (int j = 1; j <= n; j++) {
        if (!c[j] && !d1[i + j] && !d2[i - j + n]) {
            ans[i] = j; // 记录第i行的皇后放在了第j列
            c[j] = d1[i + j] = d2[i - j + n] = 1; // 标记
            dfs(i + 1);
            c[j] = d1[i + j] = d2[i - j + n] = 0; // 复原
        }
    }
}
int main()
{
    scanf("%d", &n);
    dfs(1);
    printf("%d\n", cnt);
    return 0;
}

宽度优先搜索（BFS）

宽搜的过程
从起点开始，向下逐层扩展，逐层访问
宽搜的实现
宽搜是通过队列实现的，用 queue 创建一个队列，在搜索过程中通过队列来维护序列的状态空间，入队就排队等待，出队就扩展后续状态入队

例：[USACO07OPEN] Catch That Cow S

5-1=4; 4*2=8; 8*2=16; 16+1=17

暴力搜索当前位置的三种移动方式
要求最小步数，应该用BFS
从起始位置x开始搜索，ans数组存储移动步数，当x==y时，ans[y]即答案

边界约束 \((1 \le x \le 10^5)\) 与去重
x*2,x-1,x-1 不如 x-1,x*2 更优，所以上界：\(x \le 10^5\)
减到 0 或负以后再加也不会更优，所以下界：\(x \ge 1\)

#include <cstdio>
#include <queue>
using namespace std;
const int MAXN = 100005;
int ans[MAXN];
int main()
{
    int t;
    scanf("%d", &t);
    while (t--) {
        for (int i = 0; i < MAXN; i++) ans[i] = -1;
        int x, y;
        scanf("%d%d", &x, &y);
        queue<int> q;
        q.push(x); ans[x] = 0;
        while (!q.empty()) {
            int cur = q.front(); q.pop();
            if (cur == y) break;
            if (cur + 1 < MAXN && ans[cur + 1] == -1) {
                ans[cur + 1] = ans[cur] + 1; q.push(cur + 1); // 前进一步
            }
            if (cur - 1 > 0 && ans[cur - 1] == -1) {
                ans[cur - 1] = ans[cur] + 1; q.push(cur - 1); // 后退一步
            }
            if (cur * 2 < MAXN && ans[cur * 2] == -1) {
                ans[cur * 2] = ans[cur] + 1; q.push(cur * 2); // 走到2倍位置
            }
        }
        printf("%d\n", ans[y]);
    }
    return 0;
}

洪水填充（flood fill）

判断连通性和统计连通块个数的问题

例：P1596 [USACO10OCT] Lake Counting S

存储网格图
f[x][y] 存储网格图
dx[8] dy[8] 存储方向偏移量
搜索
枚举单元格，判断是否可以进入
如果可以进入，则水坑数量+1，并且将该单元格所属水坑的其他单元格全都进入一遍（这里DFS和BFS都可实现）
为避免重复搜索，对走过的单元格进行标记

DFS实现

#include <cstdio>
char f[105][105];
int n, m;
int dx[8] = {-1, -1, -1, 0, 0, 1, 1, 1};
int dy[8] = {-1, 0, 1, -1, 1, -1, 0, 1};
void dfs(int x, int y) {
    f[x][y] = '.';
    for (int i = 0; i < 8; i++) {
        int xx = x + dx[i];
        int yy = y + dy[i];
        if (xx >= 0 && xx < n && yy >= 0 && yy < m && f[xx][yy] == 'W') {
            dfs(xx, yy);
        }
    }
}
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; i++) scanf("%s", f[i]);
    int lake = 0;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++) 
            if (f[i][j] == 'W') {
                lake++;
                dfs(i, j);
            }
    printf("%d\n", lake);
    return 0;
}

BFS实现

#include <cstdio>
#include <queue>
using namespace std;
char f[105][105];
int n, m;
int dx[8] = {-1, -1, -1, 0, 0, 1, 1, 1};
int dy[8] = {-1, 0, 1, -1, 1, -1, 0, 1};
struct Node {
    int x, y;
};
void bfs(int x, int y) {
    f[x][y] = '.';
    queue<Node> q;
    q.push({x, y});
    while (!q.empty()) {
        Node t = q.front(); q.pop();
        for (int i = 0; i < 8; i++) {
            int xx = t.x + dx[i], yy = t.y + dy[i];
            if (xx >= 0 && xx < n && yy >= 0 && yy < m && f[xx][yy] == 'W') {
                f[xx][yy] = '.';
                q.push({xx, yy});
            }
        }
    }
}
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; i++) scanf("%s", f[i]);
    int lake = 0;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++) 
            if (f[i][j] == 'W') {
                lake++;
                bfs(i, j);
            }
    printf("%d\n", lake);
    return 0;
}