题面

题目描述

Farmer John 计划建造 \(N\)（\(1 \leq N \leq 10^5\)）个农场，用 \(N−1\) 条道路连接，构成一棵树（也就是说，所有农场之间都互相可以到达，并且没有环）。每个农场有一头奶牛，品种为更赛牛或荷斯坦牛之一。

Farmer John 的 \(M\) 个朋友（\(1 \leq M \leq 10^5\)）经常前来拜访他。在朋友 \(i\) 拜访之时，Farmer John 会与他的朋友沿着从农场 \(A_i\) 到农场 \(B_i\) 之间的唯一路径行走（可能有 \(A_i=B_i\)）。除此之外，他们还可以品尝他们经过的路径上任意一头奶牛的牛奶。由于 Farmer John 的朋友们大多数也是农场主，他们对牛奶有着极强的偏好。他的有些朋友只喝更赛牛的牛奶，其余的只喝荷斯坦牛的牛奶。任何 Farmer John 的朋友只有在他们访问时能喝到他们偏好的牛奶才会高兴。

请求出每个朋友在拜访过后是否会高兴。

输入

输入的第一行包含两个整数 \(N\) 和 \(M\)。

第二行包含一个长为 \(N\) 的字符串。如果第 \(i\) 个农场中的奶牛是更赛牛，则字符串中第 \(i\) 个字符为 G，如果第 \(i\) 个农场中的奶牛是荷斯坦牛则为 H。

以下 \(N−1\) 行，每行包含两个不同的整数 \(X\) 和 \(Y\)（\(1 \leq X,Y \leq N\)），表示农场 \(X\) 与 \(Y\) 之间有一条道路。

以下 \(M\) 行，每行包含整数 \(A_i，B_i\)，以及一个字符 \(C_i\)。\(A_i\) 和 \(B_i\) 表示朋友 \(i\) 拜访时行走的路径的端点，\(C_i\) 是 G 或 H 之一，表示第 \(i\) 个朋友喜欢更赛牛的牛奶或是荷斯坦牛的牛奶。

输出

输出一个长为 \(M\) 的二进制字符串。如果第 \(i\) 个朋友会感到高兴，则字符串的第 \(i\) 个字符为 1，否则为 0。

样例输入输出

输入：

5 5
HHGHG
1 2
2 3
2 4
1 5
1 4 H
1 4 G
1 3 G
1 3 H
5 5 H

输出：

10110

这是笔者今天考试时的一道题，并非常蒟蒻地得了 \(56pts\)。

老师讲完后顿有所悟，故作此篇。

\(P.S.\) 复制题面+改 \(\LaTeX\) 好烦。

思考

1. 考试时思路

考试时脑子一抽，觉得要用什么高大上的算法，估摸估摸有了个 LCA。

当时的想法是，记录某个节点到根节点的“长度”，这里长度指的是把更赛牛看做 1，把荷斯坦牛看做 0，从某节点到根节点的所有节点的权值之和。然后询问时先看路径上有几个点，再看路径长度多少（LCA），然后比较一下。

最后，就得到了 \(56pts\) 的代码：（代码已丢失啊啊啊啊啊）

2. 老师讲思路

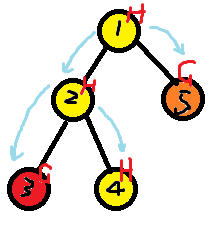
就……标色法，DFS，碰到不同种类的牛就换种颜色继续标……踢死就是所有想通的同种类的牛标记为同一种颜色（哇我好蒻居然没有想到）

于是，我兴冲冲地提交了第一份代码：

#include <bits/stdc++.h>
using namespace std;
 
const int MS=100005;
int n,m,col[MS];
int head[MS],nxt[MS*2],vet[MS*2],edgenum;
char s[MS];
void addedge(int u,int v) {
    vet[++edgenum]=v;
    nxt[edgenum]=head[u];
    head[u]=edgenum;
    return ;
}
void dfs(int u,int fa) {
    int p=0;
    for(int e=head[u];e;e=nxt[e]) {
        int v=vet[e];
        if(v==fa) continue;
        if(s[u]==s[v]) col[v]=col[u];
        else col[v]=col[u]+(++p);
        dfs(v,u);
    }
    return ;
}
char ans[MS];
 
int main() {
    scanf("%d%d%s",&n,&m,s+1);
    int x,y;
    for(int i=1;i<n;i++) {
        scanf("%d%d",&x,&y);
        addedge(x,y),addedge(y,x);
    }
    dfs(1,0);
    char ch;
    for(int i=0;i<m;i++) {
        scanf("%d%d",&x,&y);
        cin>>ch;
        if(col[x]!=col[y]||s[x]==ch) ans[i]='1';
        else ans[i]='0';
    }
    printf("%s\n",ans);
    return 0;
}

嗯嗯？为什么 \(31pts\)？其实很简单~

3. 进一步思考

首先！我发现了一个问题：当上面的程序遇到如下样例时，就会出 BUG 。

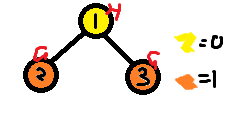
询问：2 3 H？显然，从 2 到 3 的路径上是有 H 牛的（1）。但是为什么输出 0 呢？

观察一下，发现其实 2 和 3 两点不应同为 1。为什么？因为它们并不相连。于是，我们对以上代码进行优化，添加随机数，使两个节点颜色相同的概率大大降低。

以下是代码：

#include <bits/stdc++.h>
using namespace std;

const int MS=100005;
typedef long long ll;
int n,m;
ll col[MS];
int head[MS],nxt[MS*2],vet[MS*2],edgenum;
char s[MS];
mt19937 rng(1234567);
void addedge(int u,int v) {
	vet[++edgenum]=v;
	nxt[edgenum]=head[u];
	head[u]=edgenum;
	return ;
}
void dfs(int u,int fa) {
	for(int e=head[u];e;e=nxt[e]) {
		int v=vet[e];
		if(v==fa) continue;
		if(s[u]==s[v]) col[v]=col[u];
		else col[v]=col[u]+rng();
		dfs(v,u);
	}
	return ;
}
char ans[MS];

int main() {
	scanf("%d%d%s",&n,&m,s+1);
	int x,y;
	for(int i=1;i<n;i++) {
		scanf("%d%d",&x,&y);
		addedge(x,y),addedge(y,x);
	}
	dfs(1,0);
	char ch;
	for(int i=0;i<m;i++) {
		scanf("%d%d",&x,&y);
		cin>>ch;
		if(col[x]!=col[y]||s[x]==ch) ans[i]='1';
		else ans[i]='0';
	}
	printf("%s\n",ans);
	return 0;
}

（\(max 156ms\)）

完！