Tarjan(scc)
Tarjan 算法之一是一个强连通分量算法,可以找出所有的强连通分量,时间复杂度线性。
算法中对于搜索树(如下图)作了如下定义:
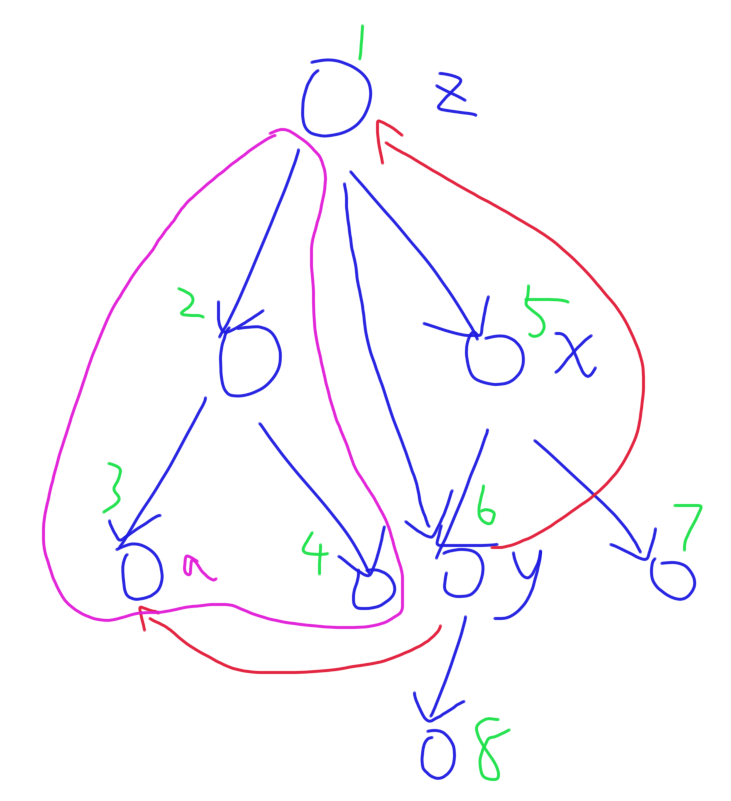
- 树枝边,即父亲与孩子的边,如 \((x,y)\)。
- 前向边,即祖先到孩子的边,如 \((z,y)\)。(树枝边属于特殊的前向边)
- 后向边,即孩子到祖先的边,如 \((y,z)\)。(与前向边相反)
- 横叉边,当前点到已经结束的搜索分支,如 \((y,a)\)。(紫色部分表示已经结束的分支)
然后一个点在某个强连通分量内的情况:
- 走了一条后向边。
- 走了一条横叉边,再走了一条后向边。
我们定义 \(dfn_u\) 表示 \(u\) 的 \(dfs\) 序,\(low_u\) 表示其子树内向上走后向边/横叉边能到达的最小 \(dfn\)。
二者的体现就是就在于走的边 \((u,v)\) 满足 \(dfn_v<dfn_u\)。
直观的感性理解:对于 \(low_u==dfn_u\),它无法向上走到任何点,说明它就是所在强连通分量的顶端,此时我们可以弹栈获取这个强连通分量(直到栈顶等于当前点 \(u\))。
栈中存储的是目前还没有完全找出的强连通分量。
void tarjan(int x){
dfn[x]=low[x]=++now;
in[x]=1;//表示在栈中
stk[++top]=x;
Ed{
int j=e[i];
if(!dfn[j]){
tarjan(j);
low[x]=min(low[x],low[j]);//由于是子节点,那么属于子树的范畴
}
else if(in[j])low[x]=min(low[x],dfn[j]);//由于是后向边/横叉边,所以不能再走,只能走到dfn(实际上写low好像也是对的)
}
if(low[x]==dfn[x]){//完整的强连通分量出现
++scc_cnt;
int y;
do{
y=stk[top--];
in[y]=0;
id[y]=scc_cnt;//表示每个点属于哪个强连通分量
}while(y!=x);
}
}
int main(){
E(i, n)
if(!dfn[i])
tarjan(i);//注意图可能不连通
}
经典例题:P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G
考虑先求强连通分量,这样一个强连通分量内的点就是两两喜欢,那么它们就同呼吸、共命运,要么都是明星,要么都不是。
我们定义缩点为一个强连通分量内的点视作一个点(原来再两个强连通分量之间的边保留,在一个强连通分量的边删去,并保留新点中有几个原点)。
此时若存在明星,必定证明只有一个点没有出边(如果超过 \(1\) 个,那么它们几个之间必然没有边,那么就不满足所有人都喜欢)。
所以我们不需要建图,只需要检查出度为 \(0\) 的点数即可。