匝谭旋替
CF1603D Artistic Partition
先解决\(c(l,r)\)
\(c(l,r)=\sum\limits_{i=l}^r\sum\limits_{j=i}^r[gcd(i,j)\ge l]=\sum\limits_{k=l}^r\sum\limits_{i=l}^r\sum\limits_{j=i}^r[gcd(i,j)=k]=\)
\(\sum\limits_{k=l}^r\sum\limits_{i=l,k|i}^r\sum\limits_{j=i,k|j}^r[gcd(\dfrac{i}{k},\dfrac{j}{k})=1]=\sum\limits_{k=l}^r\sum\limits_{i=\frac{l}{k}}^{\frac{r}{k}}\sum\limits_{j=i}^{\frac{r}{k}}[gcd(i,j)=1]\)
\(=\sum\limits_{k=l}^{r}\sum\limits_{j=1}^{\frac{r}{k}}\phi(j)\)
设\(S(n)=\sum\limits_{i=1}^n\phi(i)\)
\(c(l,r)=\sum\limits_{k=l}^rS({\dfrac{r}{k}})\)
如果固定左端点,移动\(r\)
对于\(\dfrac{r+1}{k}\),改变的就是\(r+1\)的因数会\(+1\)
同时注意到,对于\(k>log_2(n)\)的,可以用\(c(l,2l-1)=l\)来保证答案为\(r-l+1\),可以发现这时能取到的最小值,所以只用考虑\(k\le log_2(n)\)
直接\(dp\),线段树优化即可,我们这里因为要枚举因数所以时间复杂度是\(O(n\ln(n)\log^2(n))\)
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+5;
vector<int>D[MAXN];
int prime[MAXN];
int cnt_prime;
int phi[MAXN];
int vis[MAXN];
void Euler(int X)
{
vis[0]=vis[1]=1;
phi[1]=1;
for(int i=2;i<=X;i++)
{
if(!vis[i])
{
prime[++cnt_prime]=i;
phi[i]=i-1;
}
for(int j=1;j<=cnt_prime&&prime[j]*i<=X;j++)
{
vis[i*prime[j]]=1;
if(i%prime[j]==0)
{
phi[i*prime[j]]=(prime[j]*phi[i]);
break;
}
else
{
phi[i*prime[j]]=(prime[j]-1)*phi[i];
}
}
}
}
int n,k,t;
struct Seg{
int l,r;
long long lazy;
long long date;
}Tree[MAXN*4];
long long dp[MAXN][25];
int p;
void Build(int k)
{
p=1;
while(p<n+2)
{
p*=2;
}
for(int i=1;i<=p+n+1;i++)
{
Tree[i].date=1e15;
Tree[i].lazy=0;
}
for(int i=p+1;i<=p+n+1;i++)
{
Tree[i].date=dp[i-p-1][k];
}
for(int i=p+1+n;i>=1;i--)
{
Tree[i>>1].date=min(Tree[i>>1].date,Tree[i].date);
}
}
void Update(int l,int r,int val)
{
int Ls=p+l-1;
int Rs=p+r+1;
for(;(Ls^Rs)!=1;Ls>>=1,Rs>>=1)
{
if(!(Ls&1))
{
Tree[Ls^1].date+=val;
Tree[Ls^1].lazy+=val;
}
if((Rs&1))
{
Tree[Rs^1].date+=val;
Tree[Rs^1].lazy+=val;
}
Tree[Ls>>1].date=min(Tree[Ls].date,Tree[Ls^1].date)+(Tree[Ls>>1].lazy);
Tree[Rs>>1].date=min(Tree[Rs].date,Tree[Rs^1].date)+(Tree[Rs>>1].lazy);
}
for(;Ls!=1;Ls>>=1)
{
Tree[Ls>>1].date=min(Tree[Ls].date,Tree[Ls^1].date)+(Tree[Ls>>1].lazy);
//printf("%d %d???\n",Tree[1].date,val);
}
return;
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
Euler(MAXN-5);
for(int i=1;i<=MAXN-5;i++)
{
for(int j=i;j<=MAXN-5;j+=i)
{
D[j].push_back(i);
}
}
n=1e5;
for(int i=1;i<=n;i++)
{
dp[i][0]=1e15;
}
dp[0][0]=0;
for(int px=1;px<=20;px++)
{
Build(px-1);
for(int i=1;i<=n;i++)
{
for(int j=0;j<D[i].size();j++)
{
int v=D[i][j];
Update(1,v,phi[i/v]);
}
dp[i][px]=Tree[1].date;
}
}
scanf("%d",&t);
while(t--)
{
scanf("%d %d",&n,&k);
if(k>log2(n))
{
printf("%d\n",n);
}
else
{
printf("%lld\n",dp[n][k]);
}
}
}
「EC Final 2018」异国情调的……古城 / Exotic … Ancient City
一个很有趣的题
一个很直觉的思路,每次增加的层所要的贡献是一定的,不过好像是错的,大概是因为每次增加的层的上一层已经有一定的连通性,所以上一层的方案复制过来可能初始状态不同
这启示我们关注上一层的联通性
如果加边肯定是从大到小加,这里加边层与层之间要重新加
由于边权只有\(30\),考虑计算边权\(\le w\)的使用情况,这里让他们没差别全用上,这样就可得到\(>w\)的使用情况
现在我们加边,先处理第一层的连边,对于第二层,我们先复制第一层的连边情况,再考虑,左侧的点已经有一部分是联通的,我们可以考虑记录上一层右侧点的联通情况并作为新加的边,来判断是否需要这条边,差分一下即可
时间复杂度好像不会证,不过新加的边貌似每次减少的很快,感觉是只会跑\(\log(n)\)次,不过是不是说明其实只用暴力\(\log(n)\)然后直接沿用错误做法即可?
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+5;
int n,M,m;
int x,y,z;
struct Edge{
int u,v;
};
int fa[MAXN*2];
int find(int x)
{
if(fa[x]==x)
{
return fa[x];
}
fa[x]=find(fa[x]);
return fa[x];
}
vector<Edge>edge[31];
long long s[MAXN];
long long Ans[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d %d",&n,&M,&m);
for(int i=1;i<=m;i++)
{
scanf("%d %d %d",&x,&y,&z);
for(int j=z;j<=30;j++)
{
edge[j].push_back((Edge){x,y+n});
}
}
vector<Edge>Avil,Tmp;
for(int w=0;w<=30;w++)
{
for(int i=1;i<=2*n;i++)
{
fa[i]=i;
}
for(int i=1;i<=M;i++)
{
s[i]=0;
}
Avil.clear();
Tmp.clear();
for(int i=0;i<edge[w].size();i++)
{
int u=find(edge[w][i].u);
int v=find(edge[w][i].v);
if(u>v)
{
swap(u,v);
}
if(u!=v)
{
fa[u]=v;
s[1]++;
if((u>n)&&(v>n))
{
Avil.push_back((Edge){u-n,v-n});
}
}
}
for(int d=2;d<=M;d++)
{
Tmp.clear();
for(int i=0;i<Avil.size();i++)
{
int u=find(Avil[i].u);
int v=find(Avil[i].v);
if(u>v)
{
swap(u,v);
}
if(u!=v)
{
fa[u]=v;
if((u>n)&&(v>n))
{
Tmp.push_back((Edge){u-n,v-n});
}
}
else
{
s[d]--;
}
}
Avil=Tmp;
}
for(int i=1;i<=M;i++)
{
s[i]+=s[i-1];
}
for(int i=1;i<=M;i++)
{
s[i]+=s[i-1];
}
for(int i=1;i<=M;i++)
{
Ans[i]=Ans[i]+((long long)i+1)*n-1-s[i];
}
}
for(int i=1;i<=M;i++)
{
printf("%lld\n",Ans[i]);
}
}
[CEOI2014] The Wall
可以说是道结论题\(?\)
先给结论,围墙的方案一定包含最左上角到每个村的左上角的最短路
考虑如果不包含,考虑两种情况,相交和完全包含
完全包含肯定选最短路更优
如果是相交,那我们可以在用最短路替换一部分原有路径
可以发现替换的和上面村的位置有关,具体的我们要保留贴着上面一个村的路径
但这样替换后方案就会包含这个最短路
模拟这个过程你会发现其实最后的方案就是要包含整个最短路树,所以我们的路径贴着它就可以了,而且你会发现这样就是合法的
但这样还是不好做,考虑再把每个点拆成四个点,这四个点不能穿过最短路树,如果这样跑最小环,其实就是在贴着最短路树跑
Show Code
#include<bits/stdc++.h>
#define INF 1e16
using namespace std;
const int MAXN=505;
int n,m;
int a[MAXN][MAXN];
int A[MAXN][MAXN];
int valx[MAXN][MAXN];
int valy[MAXN][MAXN];
struct Edgex{
int vx,vy;
int val;
};
vector<Edgex>G[MAXN][MAXN];
struct nodex{
int x,y;
long long val;
bool operator<(const nodex p)const{
return val>p.val;
}
};
long long dpx[MAXN][MAXN];
int visx[MAXN][MAXN];
int zfx[5]={0,0,1,-1};
int zfy[5]={1,-1,0,0};
void dijkstrax(int x,int y)
{
for(int i=1;i<=n+1;i++)
{
for(int j=1;j<=m+1;j++)
{
dpx[i][j]=INF;
visx[i][j]=0;
}
}
dpx[x][y]=0;
priority_queue<nodex>q;
q.push((nodex){x,y,0});
while(q.size())
{
nodex temp=q.top();
q.pop();
if(visx[temp.x][temp.y])
{
continue;
}
visx[temp.x][temp.y]=1;
for(int i=0;i<G[temp.x][temp.y].size();i++)
{
int vx=G[temp.x][temp.y][i].vx;
int vy=G[temp.x][temp.y][i].vy;
int w=G[temp.x][temp.y][i].val;
if(dpx[vx][vy]>dpx[temp.x][temp.y]+w)
{
dpx[vx][vy]=dpx[temp.x][temp.y]+w;
q.push((nodex){vx,vy,dpx[vx][vy]});
}
}
}
}
vector<Edgex>Rg[MAXN][MAXN];
int Rd[MAXN][MAXN];
int Clor[MAXN][MAXN][2][2];
int Cnt_id;
int Id[MAXN][MAXN][2][2];
struct Edge{
int v,val;
};
long long dp[MAXN*MAXN*5];
int vis[MAXN*MAXN*5];
vector<Edge>g[MAXN*MAXN*5];
struct node{
int u;
long long val;
bool operator<(const node x)const{
return val>x.val;
}
};
void dijkstra(int s)
{
for(int i=1;i<=Cnt_id;i++)
{
dp[i]=INF;
vis[i]=0;
}
priority_queue<node>q;
q.push((node){s,0});
dp[s]=0;
while(q.size())
{
node temp=q.top();
q.pop();
if(vis[temp.u])
{
continue;
}
//printf("%d %d %d %d %d?????\n",dp[temp.u],Rec[temp.u].first.first,Rec[temp.u].first.second,Rec[temp.u].second.first,Rec[temp.u].second.second);
vis[temp.u]=1;
for(int i=0;i<g[temp.u].size();i++)
{
int v=g[temp.u][i].v;
int w=g[temp.u][i].val;
//printf("%d %d %d %d---uf\n",Rec[v].first.first,Rec[v].first.second,Rec[v].second.first,Rec[v].second.second);
if(dp[v]>dp[temp.u]+w)
{
dp[v]=dp[temp.u]+w;
q.push((node){v,dp[v]});
}
}
}
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
int Cnt=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
A[i][j]=a[i][j];
++Cnt;
}
}
//printf("%d??\n",Cnt);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m+1;j++)
{
scanf("%d",&valx[i][j]);
}
}
for(int i=1;i<=n+1;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&valy[i][j]);
}
}
for(int i=1;i<=n+1;i++)
{
for(int j=1;j<=m+1;j++)
{
if(i+1<=n+1)
{
G[i][j].push_back((Edgex){i+1,j,valx[i][j]});
G[i+1][j].push_back((Edgex){i,j,valx[i][j]});
}
if((j+1)<=m+1)
{
G[i][j].push_back((Edgex){i,j+1,valy[i][j]});
G[i][j+1].push_back((Edgex){i,j,valy[i][j]});
}
}
}
dijkstrax(1,1);
for(int i=1;i<=n+1;i++)
{
for(int j=1;j<=m+1;j++)
{
for(int k=0;k<G[i][j].size();k++)
{
int vx=G[i][j][k].vx;
int vy=G[i][j][k].vy;
int w=G[i][j][k].val;
if(dpx[vx][vy]==dpx[i][j]+w)
{
Rd[i][j]++;
Rg[vx][vy].push_back((Edgex){i,j,0});
}
}
}
}
queue<pair<int,int> >q;
for(int i=1;i<=n+1;i++)
{
for(int j=1;j<=m+1;j++)
{
if(Rd[i][j]==0)
{
q.push(make_pair(i,j));
}
}
}
while(q.size())
{
pair<int,int>temp=q.front();
q.pop();
for(int i=0;i<Rg[temp.first][temp.second].size();i++)
{
int vx=Rg[temp.first][temp.second][i].vx;
int vy=Rg[temp.first][temp.second][i].vy;
Rd[vx][vy]--;
if(!Rd[vx][vy])
{
q.push(make_pair(vx,vy));
}
if(A[temp.first][temp.second])
{
int Dir=((temp.first!=vx));
int Tox;
if(Dir)
{
Tox=(temp.first<vx);
}
else
{
Tox=(temp.second<vy);
}
// printf("%d %d %d %d??\n",temp.first,temp.second,Tox,Dir);
// printf("%d %d %d %d??\n",vx,vy,Tox^1,Dir);
Clor[temp.first][temp.second][Tox][Dir]=1;
Clor[vx][vy][Tox^1][Dir]=1;
A[vx][vy]=1;
}
}
}
Cnt_id=0;
for(int i=1;i<=n+1;i++)
{
for(int j=1;j<=m+1;j++)
{
Id[i][j][0][0]=++Cnt_id;
Id[i][j][1][0]=++Cnt_id;
Id[i][j][0][1]=++Cnt_id;
Id[i][j][1][1]=++Cnt_id;
}
}
for(int i=1;i<=n+1;i++)
{
for(int j=1;j<=m+1;j++)
{
if(i+1<=n+1)
{
g[Id[i][j][1][0]].push_back((Edge){Id[i+1][j][0][0],valx[i][j]});
g[Id[i+1][j][0][0]].push_back((Edge){Id[i][j][1][0],valx[i][j]});
g[Id[i][j][1][1]].push_back((Edge){Id[i+1][j][0][1],valx[i][j]});
g[Id[i+1][j][0][1]].push_back((Edge){Id[i][j][1][1],valx[i][j]});
}
if(j+1<=m+1)
{
g[Id[i][j][0][1]].push_back((Edge){Id[i][j+1][0][0],valy[i][j]});
// printf("%d %d???\n",Id[i][j][0][1],Id[i][j+1][0][0]);
g[Id[i][j+1][0][0]].push_back((Edge){Id[i][j][0][1],valy[i][j]});
g[Id[i][j][1][1]].push_back((Edge){Id[i][j+1][1][0],valy[i][j]});
g[Id[i][j+1][1][0]].push_back((Edge){Id[i][j][1][1],valy[i][j]});
}
if((!Clor[i][j][0][1])&&(!a[i-1][j])&&(!a[i-1][j-1])&&(!(i==1&&j==1)))
{
g[Id[i][j][0][0]].push_back((Edge){Id[i][j][0][1],0});
g[Id[i][j][0][1]].push_back((Edge){Id[i][j][0][0],0});
}
if((!Clor[i][j][1][0])&&(!a[i][j])&&(!a[i-1][j]))
{
// if(i==1&&j==4)
// {
// printf("ufc???\n");
// }
g[Id[i][j][1][1]].push_back((Edge){Id[i][j][0][1],0});
g[Id[i][j][0][1]].push_back((Edge){Id[i][j][1][1],0});
}
if((!Clor[i][j][1][1])&&(!a[i][j])&&(!a[i][j-1]))
{
g[Id[i][j][1][1]].push_back((Edge){Id[i][j][1][0],0});
g[Id[i][j][1][0]].push_back((Edge){Id[i][j][1][1],0});
}
// if(i==3&&j==2)
// {
// printf("%d %d %dfuckufkc\n",(!Clor[i][j][0][0]),(!a[i-1][j-1]),(!a[i][j-1]));
// }
if((!Clor[i][j][0][0])&&(!a[i-1][j-1])&&(!a[i][j-1])&&(!(i==1&&j==1)))
{
// if(i==3&&j==2)
// {
// printf("fuckufkc\n");
// }
g[Id[i][j][0][0]].push_back((Edge){Id[i][j][1][0],0});
g[Id[i][j][1][0]].push_back((Edge){Id[i][j][0][0],0});
}
}
}
dijkstra(Id[1][1][0][1]);
printf("%lld\n",dp[Id[1][1][1][0]]);
}
[ICPC2014 WF] Baggage
当草稿了,最开始想用\(n=3\)构造全部方案的,结果\(n=3\)就是要特殊构造的/kk
实际上是递归构造
Show Code
#include<bits/stdc++.h>
using namespace std;
int n;
void Print(int x,int y)
{
printf("%d to %d\n",x,y);
return;
}
void solve(int l,int r)
{
if((r-l+1)<=4)
{
return;
}
if(r-l+1==10)
{
Print(r-2,l-2);
Print(l+2,r-2);
Print(r-4,l+2);
Print(l-1,r-4);
Print(r-1,l-1);
return ;
}
if(r-l+1==12)
{
Print(r-2,l-2);
Print(r-5,r-2);
Print(l+1,r-5);
Print(r-6,l+1);
Print(l-1,r-6);
Print(r-1,l-1);
return ;
}
if(r-l+1==14)
{
Print(l+7,l-2);
Print(l+4,l+7);
Print(l+11,l+4);
Print(l+2,l+11);
Print(l+8,l+2);
Print(l-1,l+8);
Print(l+12,l-1);
return ;
}
Print(r-2,l-2);
Print(l+2,r-2);
solve(l+4,r-4);
Print(l-1,r-5);
Print(r-1,l-1);
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
if(n==3)
{
Print(2,-1);
Print(5,2);
Print(3,-3);
return 0;
}
solve(1,2*n);
}
[省选联考 2023] 城市建造
一个质量非常高的题
首先肯定和联通性有关
然后你会发现一个点双内的点要么全选,要么只能选一个
为什么边双不行?
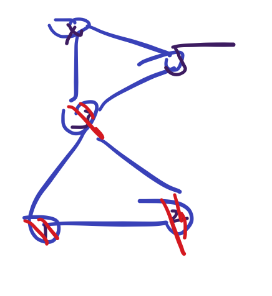
)
如图,\(1,2,3\)选了,\(4,5\)就不和\(1,2,3\)联通了
然后建圆方树
注意到选的点必须是联通的,不然就会有选的点依旧联通
这里有结论,重心一定会被选择,证明就不会了/kk
这里我们可以发现选择一个点双,就是选择一个方点断掉和它连边
这里我们钦定圆点为根,然后选择一个方点他的所有祖先都要选
考虑如果\(k=0\),枚举联通块大小\(x\),可以发现如果当前方点\(u\)子树内的圆点数\(Siz_u>x\),那一定会断\(u\),然后\(u\)的祖先也必须全断
然后\(Siz_u<x\)也一定不能断
如果\(Siz_u=x\),必须讨论一下,如果\(u\)的儿子数大于\(1\),\(u\)就一定不能断,实际上就说明无解了
如果刚好为\(1\),说明\(u\)必须断
这里可以考虑用并查集维护,枚举\(x\),因此连边即可
如果\(k=1\),这里可以容斥一下,算一下大小为\(x,x+1\)的方案数
其实也差不多,\(Siz_u>x\)直接断就好了,因为对于\(x+1\)不断一定无解
最后要特殊考虑\(Siz_u=x\)的情况,因为儿子数等于\(1\)的情况不一定必须断,方案数比较多也是由此
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
const int MOD=998244353;
int n,m,k;
int x,y;
vector<int>g[MAXN];
int dfn[MAXN];
int low[MAXN];
int cnt_dfn;
int cnt_node;
stack<int>st;
vector<int>G[MAXN];
void dfs(int x,int f)
{
dfn[x]=++cnt_dfn;
low[x]=dfn[x];
st.push(x);
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
if(v==f)
{
continue;
}
if(dfn[v])
{
low[x]=min(low[x],dfn[v]);
}
else
{
dfs(v,x);
low[x]=min(low[x],low[v]);
if(dfn[x]<=low[v])
{
++cnt_node;
G[cnt_node].push_back(x);
G[x].push_back(cnt_node);
while(st.size())
{
G[cnt_node].push_back(st.top());
G[st.top()].push_back(cnt_node);
if(st.top()==v)
{
st.pop();
break;
}
st.pop();
}
}
}
}
}
int Siz[MAXN];
int Heart;
int Mini=0x3f3f3f3f;
int Sum;
int Fa[MAXN];
void Find_Heart(int x,int f)
{
Siz[x]=(x<=n);
int Maxs=0;
Fa[x]=f;
for(int i=0;i<G[x].size();i++)
{
int v=G[x][i];
if(v==f)
{
continue;
}
Find_Heart(v,x);
Siz[x]+=Siz[v];
Maxs=max(Maxs,Siz[v]);
}
Maxs=max(Maxs,Sum-Siz[x]);
if(Mini>Maxs)
{
Mini=Maxs;
Heart=x;
}
}
vector<int>Rec[MAXN];
int fa[MAXN];
int siz[MAXN];
int Cntx[MAXN];
int find(int x)
{
if(fa[x]==x)
{
return x;
}
fa[x]=find(fa[x]);
return fa[x];
}
void unionn(int i,int j){
int ex=find(i);
int ey=find(j);
if(ex!=ey)
{
Cntx[siz[ex]]--;
Cntx[siz[ey]]--;
fa[ex]=ey;
siz[ey]+=siz[ex];
Cntx[siz[ey]]++;
siz[ex]=0;
}
}
int Res1[MAXN];
int Res2[MAXN];
int Tot[MAXN];
int Vis[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d %d",&n,&m,&k);
for(int i=1;i<=m;i++)
{
scanf("%d %d",&x,&y);
g[x].push_back(y);
g[y].push_back(x);
}
cnt_node=n;
dfs(1,0);
Sum=n;
Find_Heart(1,0);
if(Heart>n)
{
Heart=G[Heart][0];
}
Mini=0;
Find_Heart(Heart,0);
for(int i=n+1;i<=cnt_node;i++)
{
Rec[Siz[i]].push_back(i);
}
for(int i=1;i<=n;i++)
{
fa[i]=i;
siz[i]=1;
Cntx[siz[i]]++;
}
for(int i=1;i<n;i++)
{
//printf("%d???\n",Cntx[1]);
for(int j=0;j<Rec[i].size();j++)
{
int v=Rec[i][j];
if(G[v].size()>2)
{
for(int k=1;k<G[v].size();k++)
{
unionn(G[v][k],G[v][k-1]);
}
}
}
Res1[i]=(Cntx[i]*i==n);
vector<int>V;
for(int j=0;j<Rec[i].size();j++)
{
int v=Rec[i][j];
if(G[v].size()==2)
{
if(siz[Fa[v]]==1)
{
V.push_back(Fa[v]);
Vis[v]=1;
for(int k=1;k<G[v].size();k++)
{
unionn(G[v][k],G[v][k-1]);
}
++Tot[Fa[v]];
}
else if(Tot[Fa[v]])
{
++Tot[Fa[v]];
}
}
}
if(Cntx[i]*i+Cntx[i+1]*(i+1)==n)
{
Res2[i]=1;
for(int j=0;j<V.size();j++)
{
Res2[i]=((long long)Res2[i]*(Tot[V[j]]+(i==1)))%MOD;
}
}
V.clear();
for(int j=0;j<Rec[i].size();j++)
{
int v=Rec[i][j];
if(G[v].size()==2&&(!Vis[v]))
{
for(int k=1;k<G[v].size();k++)
{
unionn(G[v][k],G[v][k-1]);
}
}
}
}
int Res=0;
if(k==0)
{
for(int i=1;i<n;i++)
{
Res+=Res1[i];
}
printf("%d\n",Res);
}
else
{
for(int i=1;i<n;i++)
{
Res=((long long)Res+Res2[i])%MOD;
}
for(int i=1;i<n;i++)
{
Res=((long long)Res-Res1[i]+MOD)%MOD;
}
printf("%d\n",Res);
}
}
CF1852D Miriany and Matchstick
\(S\)本身就有的我们先剔除,只用考虑\(T\)之间左右相邻的和\(S,T\)之间上下相邻
\(O(n^2)\)的暴力\(dp\)似乎很显,这里当然也可以\(bitset\)优化一下
具体的就是\(dp_{i,j,0}\)为第\(i\)位填\(0\)时有\(j\)对不同的是否可行,\(dp_{i,j,1}\)同理
我们这里可以考虑探究一下固定\(i\),\(j\)之间是否有性质
我们设\(dp_{i,0}\)为满足的\(j\)构成的集合
结论:\(dp_{i,0}\)和\(dp_{i,1}\)均是一个区间但有可能中间被挖去一个值\(v\)
这个可以打表找出来吧。。
注意到\(dp_{i,0},dp_{i,1}\)是一直重叠的
考虑归纳证明,边界就不管了,\(i=2\)的情况可以下去自己手算一下,\(i=1\)的情况可以先不管
对于\(i\),这里我们可以先观察一下转移,可以发现区间取并时只用关注\(0/1\)的相对位置,随便一个平移一下就行了,抽象为
\(dp_{i,0}=dp_{i-1,0}\cup(dp_{i-1,1}+1)\)
\(dp_{i,1}=dp_{i-1,1}\cup(dp_{i-1,0}+1)+(\pm1)\)
这里就只先解决这种情况,其他的同理,\(0/1\)整体平移一下即可
首先对于\(x\in dp_{i-1,0},dp_{i-1,1}\)
可以发现\(dp_{i,0}\)产生的是\(\{x,x+1\}\),\(dp_{i,1}\)产生的是\(\{x+1,x+2\}\)或者\(\{x,x-1\}\)依旧有重叠部分
所以\(0/1\)始终有重叠
那这里缺的位置是只有原有区间来产生,不会因为并产生空
可以假定这里缺的位置不能是端点,因为是端点一定能被填上或者可以忽略
那么对于缺的位置还有一个更强的结论,对于一个\(0\)缺的位置\(v\),\(v+1\)或\(v-1\)一定会出现在\(1\)中
当然换一下也是成立的
这里同样归纳证明
如果\(v+1\)出现在\((i-1,1)\)中,那\((0,i)\)就缺\(v\),\((1,i)\)什么都不缺
如果\(v-1\)出现在\((i-1,1)\)中,那\((0,i)\)什么都不缺,\((1,i)\)缺\(v/v+2\),但\(v+2\)还是\(v\)在\((0,i)\)中都有\(v+1\)相邻
由此,如果\(i=2\)只有一个缺口,每次操作后最多也只会有一个缺口
最后直接\(O(n)\)转移即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int t;
int n,k;
char s[MAXN];
struct Node{
int l,r,p;
}dp[MAXN][2];
bool Contain(Node t,int x)
{
if(t.l<=x&&t.r>=x&&x!=t.p)
{
return 1;
}
return 0;
}
Node operator+(const Node x,const Node y)
{
Node Tx;
Tx.l=min(x.l,y.l);
Tx.r=max(x.r,y.r);
Tx.p=0;
if(x.p&&(!Contain(y,x.p)))
{
Tx.p=x.p;
}
if(y.p&&(!Contain(x,y.p)))
{
Tx.p=y.p;
}
if(x.r>y.r)
{
if(y.r+2==x.l)
{
Tx.p=y.r+1;
}
}
else
{
if(x.r+2==y.l)
{
Tx.p=x.r+1;
}
}
return Tx;
}
Node Shift(Node t,int x)
{
return (Node){t.l+x,t.r+x,(t.p)?(t.p+x):0};
}
int Ans[MAXN];
void Print(int i,int k,int op)
{
Ans[i]=op;
if(i==1)
{
return;
}
if(s[i]=='A')
{
if(op==0)
{
if(Contain(dp[i-1][0],k))
{
Print(i-1,k,0);
}
else if(Contain(Shift(dp[i-1][1],1),k))
{
Print(i-1,k-1,1);
}
}
else
{
if(Contain(Shift(dp[i-1][0],2),k))
{
Print(i-1,k-2,0);
}
else if(Contain(Shift(dp[i-1][1],1),k))
{
Print(i-1,k-1,1);
}
}
}
else
{
if(op==0)
{
if(Contain(Shift(dp[i-1][0],1),k))
{
Print(i-1,k-1,0);
}
else if(Contain(Shift(dp[i-1][1],2),k))
{
Print(i-1,k-2,1);
}
}
else
{
if(Contain(Shift(dp[i-1][0],1),k))
{
Print(i-1,k-1,0);
}
else if(Contain(dp[i-1][1],k))
{
Print(i-1,k,1);
}
}
}
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&t);
while(t--)
{
scanf("%d %d",&n,&k);
scanf("%s",s+1);
for(int i=1;i<n;i++)
{
if(s[i]!=s[i+1])
{
k--;
}
}
if(k<0)
{
printf("NO\n");
continue;
}
dp[1][0]=(Node){(s[1]=='B'),(s[1]=='B'),-1};
dp[1][1]=(Node){(s[1]=='A'),(s[1]=='A'),-1};
for(int i=2;i<=n;i++)
{
if(s[i]=='A')
{
dp[i][0]=dp[i-1][0]+Shift(dp[i-1][1],1);
dp[i][1]=Shift(dp[i-1][0],2)+Shift(dp[i-1][1],1);
}
else
{
dp[i][0]=Shift(dp[i-1][0],1)+Shift(dp[i-1][1],2);
dp[i][1]=Shift(dp[i-1][0],1)+dp[i-1][1];
}
}
if(Contain(dp[n][0],k))
{
printf("YES\n");
Print(n,k,0);
for(int i=1;i<=n;i++)
{
if(Ans[i])
{
printf("B");
}
else
{
printf("A");
}
}
printf("\n");
}
else if(Contain(dp[n][1],k))
{
printf("YES\n");
Print(n,k,1);
for(int i=1;i<=n;i++)
{
if(Ans[i])
{
printf("B");
}
else
{
printf("A");
}
}
printf("\n");
}
else
{
printf("NO\n");
}
}
}
[ARC100F] Colorful Sequences
分析一下问题,可以发现瓶颈在于限制牛仔序列
前\(20pts\)似乎直接状压+子序列DP即可
\(sub3\)是个很好的启发,由于\(A\)就是牛仔序列,我们只需要统计每个\(A\)的贡献
直接枚举\(A\)的位置算方案数,答案是\((n-m+1)k^{n-m}\)
\(sub4\)我们先剔除\(m=n\)的情况
剩下的,考虑容斥,先计算所有\(A\)可能的贡献\((n-m+1)k^{n-m}\),最后减去没有牛仔序列的序列中\(A\)的贡献
注意到没有牛仔序列等价于不存在连续的长度为\(K\)元素不同的段
同样考虑子序列\(dp\)
设\(dp_{i,j}\)表示填前\(i\)个数后末尾有长度为\(j\)连续的元素不同的段的方案数
转移的话考虑
\(j\rightarrow j+1\),即填上前面\(j\)个没出现的数,转移系数为\(k-j\)
\(j\rightarrow p,(p\le j)\),即填上前面出现的数,根据与末尾的位置决定\(p\)
这里直接后缀和优化即可,这里我们只需限制\(j<k\)即可保证无牛仔序列
注意这里计算的是牛度,我们可以发现每个元素均是等价的,所以我们可以计算所有长度为\(m\)元素不同的段的贡献最后除\(\dfrac{fac_k}{fac_{k-m}}\),对于这个的计算,可以记录一个辅助数组表示牛度,转移是一样的,就是最后\(j\ge m\)时要算上自己的贡献
其实这里离正解就不远了,可以发现就只剩一种情况:\(A\)中有相同元素
如果\(A\)有相同元素,一个合法的牛仔序列一定不会横跨\(A\),因此我们可以考虑直接枚举\(A\)的匹配位置算方案数
可以发现这个可以借助上面的\(dp\)的定义和转移,唯一的区别在于初值不同
时间复杂度\(O(nk)\)
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MOD=1e9+7;
const int MAXN=25005;
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int inv(int a,int p)
{
return Pow(a,p-2,p);
}
int n,K,m;
int A[MAXN];
int Vis[405];
int fac[MAXN];
int f[MAXN][405];
int g[MAXN][405];
int Sf[MAXN][405];
int Sg[MAXN][405];
int Pf[MAXN][405];
int Pg[MAXN][405];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
fac[0]=1;
for(int i=1;i<=MAXN-5;i++)
{
fac[i]=((long long)fac[i-1]*i)%MOD;
}
scanf("%d %d %d",&n,&K,&m);
if(K>n)
{
printf("0");
return 0;
}
for(int i=1;i<=m;i++)
{
scanf("%d",&A[i]);
}
bool found=0;
int Res=((long long)(n-m+1)*Pow(K,n-m,MOD))%MOD;
for(int i=1;i<=m;i++)
{
if(Vis[A[i]])
{
found=1;
}
Vis[A[i]]=1;
}
for(int i=1;i<=K;i++)
{
Vis[i]=0;
}
bool gpg=0;
for(int i=1;i<=m;i++)
{
if(i+K-1<=m)
{
bool pg=1;
for(int j=i;j<=i+K-1;j++)
{
if(Vis[A[j]])
{
pg=0;
break;
}
Vis[A[j]]=1;
}
if(pg)
{
gpg=1;
}
for(int j=i;j<=i+K-1;j++)
{
Vis[A[j]]=0;
}
}
}
if(gpg)
{
printf("%d\n",Res);
return 0;
}
for(int i=1;i<=K;i++)
{
Vis[i]=0;
}
if(found)
{
int L=0;
for(int i=1;i<=m;i++)
{
if(Vis[A[i]])
{
break;
}
++L;
Vis[A[i]]=1;
}
int R=0;
for(int i=1;i<=K;i++)
{
Vis[i]=0;
}
for(int i=m;i>=1;i--)
{
if(Vis[A[i]])
{
break;
}
++R;
Vis[A[i]]=1;
}
f[0][L]=1;
for(int i=1;i<=L;i++)
{
Sf[0][i]=1;
}
for(int i=L;i<K;i++)
{
Pf[0][i]=1;
}
g[0][R]=1;
for(int i=1;i<=R;i++)
{
Sg[0][i]=1;
}
for(int i=R;i<K;i++)
{
Pg[0][i]=1;
}
//printf("%d %d????\n",L,R);
for(int i=1;i<=n;i++)
{
for(int j=1;j<K;j++)
{
f[i][j]=((long long)f[i][j]+((long long)f[i-1][j-1]*(K-(j-1)))%MOD)%MOD;
f[i][j]=((long long)f[i][j]+Sf[i-1][j])%MOD;
g[i][j]=((long long)g[i][j]+((long long)g[i-1][j-1]*(K-(j-1)))%MOD)%MOD;
g[i][j]=((long long)g[i][j]+Sg[i-1][j])%MOD;
Pf[i][j]=((long long)Pf[i][j-1]+f[i][j])%MOD;
Pg[i][j]=((long long)Pg[i][j-1]+g[i][j])%MOD;
}
for(int j=K-1;j>=1;j--)
{
Sf[i][j]=((long long)Sf[i][j+1]+f[i][j])%MOD;
Sg[i][j]=((long long)Sg[i][j+1]+g[i][j])%MOD;
}
}
for(int i=1;i<=n-m+1;i++)
{
int l=i;
int r=l+m-1;
int Rsl=Pf[l-1][K-1];
int Rsr=Pg[n-r][K-1];
//printf("%d %d %d??\n",i,Rsl,Rsr);
Rsl=((long long)Rsl*Rsr)%MOD;
Res=((long long)Res-Rsl+MOD)%MOD;
}
printf("%d",Res);
}
else
{
f[0][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<K;j++)
{
f[i][j]=((long long)f[i][j]+((long long)f[i-1][j-1]*(K-(j-1)))%MOD)%MOD;
g[i][j]=((long long)g[i][j]+((long long)g[i-1][j-1]*(K-(j-1)))%MOD)%MOD;
f[i][j]=((long long)f[i][j]+Sf[i-1][j])%MOD;
g[i][j]=((long long)g[i][j]+Sg[i-1][j])%MOD;
if(j>=m)
{
g[i][j]=((long long)g[i][j]+f[i][j])%MOD;
}
Pf[i][j]=((long long)Pf[i][j-1]+f[i][j])%MOD;
}
for(int j=K-1;j>=1;j--)
{
Sf[i][j]=((long long)Sf[i][j+1]+f[i][j])%MOD;
Sg[i][j]=((long long)Sg[i][j+1]+g[i][j])%MOD;
}
}
int Tot=0;//////
for(int i=1;i<K;i++)
{
Tot=((long long)Tot+g[n][i])%MOD;
}
int Tkg=((long long)fac[K]*inv(fac[K-m],MOD))%MOD;
Tot=((long long)Tot*inv(Tkg,MOD))%MOD;
Res=((long long)Res-Tot+MOD)%MOD;
printf("%d",Res);
}
}