【垫底模拟】CSP-12
一场比赛题解好像必须需要一张头图:
T1 随
不会球教。
T2 便
首先明确:
-
子串是连续的
-
子序列是不连续的,可以去掉其中的任意几个元素。
如:子串\(hellloworld\) 中子序列 \(helloworld\) 出现了 \(3\) 次。
设 \(f_{i,j}\) 是表示 \(S\) 的 子串 \([1,i]\) 中匹配到目标串 \(helloworld\) 的第 \(j\) 位的 子序列 数的期望数量,有:
-
当 \(S_i\) 已经确定了,如果 \(S_i\) 没有和第 \(j\) 位匹配,这一位对于匹配到 \(j\) 位的方案数量是不变的,即 \(f_{i,j}=f{i-1,j}\)。
-
当 \(S_i\) 已经确定了,如果 \(S_i\) 和 第 \(j\) 位匹配了,那么这一位可以与第 \(j\) 位置匹配,由 \(j-1\) 的状态转移过来,即 \(f_{i,j}=f_{i-1,j}+f_{i-1,j-1}\)。
-
如果 \(S_i\) 不确定,那么这一位有可能是匹配的,也可能是不匹配的 即 \(f_{i,j}=f_{i-1,j}+p_j\times f_{i-1,j-1}\)
设 \(S\) 是子串,\(P\) 是目标串,\(p_j\) 是匹配的概率,有:
然后因为我们的目标串是 \(11\) 位,所以复杂度应该是 \(O(11\times n)\),因为我们 \(q\) 次询问次次边定与不定,所以总时间复杂度应是 \(O(11\times n\times q)\) 约为 \(10^11\)。
所以考虑转化矩阵进行优化。
因为我们的答案要在 \(j==11\) 上查询,其他状态只是用来转移,可以用矩阵代替,即:
设 \(f_i\) 是一个行数为 \(11\) 的列数为 \(1\) 的列向量,而 \(11\times 11\) 大小的矩阵 \(A_i\) 表示转换关系,设 \(f_i=f_{i-1}\times A_i\)。
或者这样理解:
众所周知,\(n\times m\) 的矩阵 \(A\) 乘上 \(m\times k\) 的矩阵 \(B\) 等于 \(n\times k\) 的矩阵 \(C\)。
那么 \(1\times 11\) 的列向量 \(f_i\) 乘上 \(11\times 11\) 的矩阵 \(B\) 可以得到最终矩阵 \(1\times 11\) 表示最终状态。
而我们的矩阵乘法是 \(C[i][j]=A[i][0] \times B[0][j]+A[i][1] \times B[1][j]+\) …… \(+A[i][m-1] \times B[m-1][j]\),即 \(A\) 的一行乘 \(B\) 的一列。
于是有列向量运算:
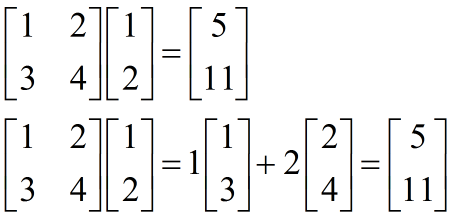
有关矩阵与向量乘积
重复一遍:设 \(f_i\) 是一个行数为 \(11\) 的列数为 \(1\) 的列向量,而 \(11\times 11\) 大小的矩阵 \(A_i\) 表示转换关系,设 \(f_i=f_{i-1}\times A_i\)。
首先,无论 \(S_i\) 是否确定,\(A_{j,j}=1\) 。
为什么?返回上面最开始的公式:
无论到底定不定,\(f_{i,j}=f_{i-1,j}+k\),根据列向量乘矩阵法则,\(A_{j,j}\) 一定是 \(1\)。(自己手模一遍吧)
然后类比去处理 \(k\) 的问题:
-
当 \(S_i\) 确定时,\(A_{j-1,j}=(S_i==T_j)\)。
-
当 \(S_i\) 不定时,\(A_{j-1,j}=p_j\)。
其余的位置都是 \(0\),它是一个三角矩阵。
用线段树维护矩阵,每次查询都是单点修改与区间查询,整挺好。
然后时间复杂度就成了 \(O(好像不能过)\)。
(\(O(11^3(n+q\times log_2^{n}\)))
最后我们再继续优化:
因为是三角矩阵,所以可以酱紫:
然后我们的测评机子由于非常寄,所以还需要继续卡时间复杂度,首先矩阵乘法要用 unsigned long long,最后再取模一次,反正就是少模几次。
其次我们的 register,inline,read之流都要上阵,但是 fread 不行,因为我们要读入字符,但是 fread 好像是一口气读入。
最后是我们的火车头(
还有一些小点,比如说 inline 在递归函数不要用会拖慢效率,mid不要写在函数开头因为可能这次不会继续向下递推,简单卡卡就能过了。
卡时间过程
(还需要一点点运气。)
下面的代码应该是稳过的,不用卡运气,(但是你运气很差也没办法)。
Miku's Code
%:pragma GCC optimize(3)
%:pragma GCC optimize("Ofast")
%:pragma GCC optimize("inline")
%:pragma GCC optimize("-fgcse")
%:pragma GCC optimize("-fgcse-lm")
%:pragma GCC optimize("-fipa-sra")
%:pragma GCC optimize("-ftree-pre")
%:pragma GCC optimize("-ftree-vrp")
%:pragma GCC optimize("-fpeephole2")
%:pragma GCC optimize("-ffast-math")
%:pragma GCC optimize("-fsched-spec")
%:pragma GCC optimize("unroll-loops")
%:pragma GCC optimize("-falign-jumps")
%:pragma GCC optimize("-falign-loops")
%:pragma GCC optimize("-falign-labels")
%:pragma GCC optimize("-fdevirtualize")
%:pragma GCC optimize("-fcaller-saves")
%:pragma GCC optimize("-fcrossjumping")
%:pragma GCC optimize("-fthread-jumps")
%:pragma GCC optimize("-funroll-loops")
%:pragma GCC optimize("-fwhole-program")
%:pragma GCC optimize("-freorder-blocks")
%:pragma GCC optimize("-fschedule-insns")
%:pragma GCC optimize("inline-functions")
%:pragma GCC optimize("-ftree-tail-merge")
%:pragma GCC optimize("-fschedule-insns2")
%:pragma GCC optimize("-fstrict-aliasing")
%:pragma GCC optimize("-fstrict-overflow")
%:pragma GCC optimize("-falign-functions")
%:pragma GCC optimize("-fcse-skip-blocks")
%:pragma GCC optimize("-fcse-follow-jumps")
%:pragma GCC optimize("-fsched-interblock")
%:pragma GCC optimize("-fpartial-inlining")
%:pragma GCC optimize("no-stack-protector")
%:pragma GCC optimize("-freorder-functions")
%:pragma GCC optimize("-findirect-inlining")
%:pragma GCC optimize("-fhoist-adjacent-loads")
%:pragma GCC optimize("-frerun-cse-after-loop")
%:pragma GCC optimize("inline-small-functions")
%:pragma GCC optimize("-finline-small-functions")
%:pragma GCC optimize("-ftree-switch-conversion")
%:pragma GCC optimize("-foptimize-sibling-calls")
%:pragma GCC optimize("-fexpensive-optimizations")
%:pragma GCC optimize("-funsafe-loop-optimizations")
%:pragma GCC optimize("inline-functions-called-once")
%:pragma GCC optimize("-fdelete-null-pointer-checks")
//火车头
#include<bits/stdc++.h>
using namespace std;
#define lid (id<<1)
#define rid (id<<1|1)
typedef unsigned long long intx;
//开ull少模几次
const int maxn=1e5+50;
const intx mod=1e9+7;
inline intx read(){
//快读
char c=getchar();
intx x=0,f=1;
while(c<48)<%if(c=='-')f=-1;c=getchar();%>
while(c>47)x=(x*10)+(c^48),c=getchar();
return x*f;
}
int T,n,q;
intx p[8],psum,pinv;
int v[12];
char P[12];
struct matrix{
intx a[12][12];
inline matrix operator*(const matrix x)const{
//矩阵乘法
matrix y;
for(register int i=0;i<=10;++i){
for(register int j=0;j<=10;++j){
y.a[i][j]=0;
for(register int k=i;k<=j;++k){
//三角矩阵
y.a[i][j]=(y.a[i][j]+a[i][k]*x.a[k][j])%mod;
}
}
}
return y;
}
};matrix mat,tr[maxn<<2],ans;
inline intx qpow(intx x,intx k){
//快速幂x^k
intx res=1;
while(k){
if(k&1) <% res=res*x%mod; %>
x=x*x%mod;
k=k>>1;
}
return res;
}
inline intx inv(intx x){
//费马小定理求逆元
return qpow(x,mod-2)%mod;
}
inline void push_up(int id){
tr[id]=tr[lid]*tr[rid];
}
void build_tree(int id,int l,int r){
if(l==r){
tr[id]=mat;
return;
}
int mid=(l+r)>>1;
build_tree(lid,l,mid);
build_tree(rid,mid+1,r);
push_up(id);
}
void update(int id,int l,int r,int pos,char c){
if(l==pos && l==r){
for(int i=0;i<=10;++i){
//确定了这个位置的字符
tr[id].a[i-1][i]=(c==P[i]);
}
return;
}
int mid=(l+r)>>1;
if(pos<=mid) update(lid,l,mid,pos,c);
else update(rid,mid+1,r,pos,c);
push_up(id);
}
void query(int id,int l,int r,int x,int y){
if(x<=l && r<=y){
ans=ans*tr[id];
return;
}
int mid=(l+r)>>1;
if(x<=mid) query(lid,l,mid,x,y);
if(y>mid) query(rid,mid+1,r,x,y);
}
inline void pre(){
P[1]='h';
P[2]='e';
P[3]=P[4]='l';
P[5]='o';
P[6]='w';
P[7]='o';
P[8]='r';
P[9]='l';
P[10]='d';
//拼出hello world目标串
v[1]=1;
v[2]=2;
v[3]=v[4]=3;
v[5]=4;
v[6]=5;
v[7]=4;
v[8]=6;
v[9]=3;
v[10]=7;
//如果说要确定为某个字符,对应转移方程中的pj
}
inline void clear(matrix &x){
//清空矩阵x并初始化矩阵,x[j,j]=1
for(register int i=0;i<=10;++i){
for(register int j=0;j<=10;++j){
x.a[i][j]=0;
}
x.a[i][i]=1;
}
}
void input(){
n=read();
for(register int i=1;i<=7;++i){
p[i]=read();
psum=psum+p[i];
}
}
int main(){
pre();
input();
pinv=inv(psum);
for(register int i=1;i<=7;++i){
//当你看到期望与概率取模或是整数的时候
p[i]=p[i]*pinv%mod;
}
clear(mat);
for(register int i=1;i<=10;++i){
//x[j-1,j]=pj
mat.a[i-1][i]=p[v[i]];
}
build_tree(1,1,n);
q=read();
int op,x,y;
char c;
while(q--){
op=read();
if(op==1){
x=read();
c=getchar();
while('a'>c) c=getchar();
update(1,1,n,x,c);
}
else{
clear(ans);
x=read();
y=read();
query(1,1,n,x,y);
printf("%lld\n",ans.a[0][10]);
}
}
return 0;
}