【自学笔记】贪婪算法解决时间安排问题(入门)
【自学笔记】贪婪算法解决时间安排问题(入门)
【前言】
笔者这几天在受学校Prolog作业折磨,在查找解决方案的时候发现了贪婪算法(Greedy Algorithm),大喜,遂尝试格物致知。本文会引用一道贪婪算法的经典例题,尝试让笔者这样的纯小白也能理解这种算法,走入精彩的“贪婪之门”。贪婪算法的教程在网上早已经星罗棋布了,不过如果你愿意,不妨花几分钟看看我的理解方法。
【定义】
贪婪算法(greedy algorithm)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解(它不能对所有问题都能得到整体最优解)。[1]
【例题】
现在有 i =11 个社团想要征用某间活动室,每个社团的活动都有不同的开始时间 si 和结束时间 fi。已知两个社团不能同时征用一个活动室,请通过代码计算出举办活动数量最大化的方法。
|
i
|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| s[i] | 1 | 3 | 0 | 5 | 3 | 5 | 6 | 8 | 8 | 2 | 12 |
| f[i] | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
【实现代码】
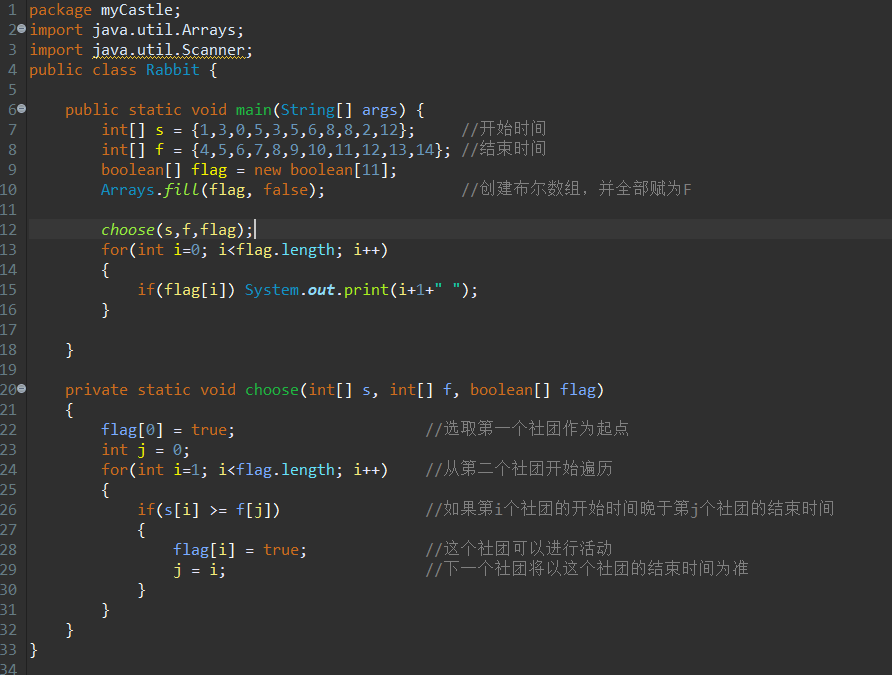
*原博主的代码为C语言,笔者在这里转换为了Java [2]
输出的结果为:1,4,8,11(恰好利用了1-14的完整的时间段)。
正在笔者愉悦地对代码进行注释的时候,发现了一行真的很难用语言形容的东西:(Line22: flag[0] = true;)。为什么一定要从第0个元素开始?前人没有留下他们的回答,但是我们不妨...
注意看,结束时间f[]是以正序排列的,从第0个元素开始恰好体现了贪婪算法的重要特征:鼠目寸光注重当下利益。面对还没有社团被批准的空空如也的社团,我们自然会认为应该把最早结束的社团活动放在最先考虑。上述代码还有可以优化的地方——如果数组f不是以正序排列呢?如果你有兴趣,不妨再加一个排序的方法来让你的程序更加完美。
参考资料
[1]贪心算法_百度百科 (baidu.com)
[2](7条消息) 贪心算法详解_lloil的博客-CSDN博客