迭代器

Iterator<Map.Entry<Integer, String>> iterator = map.entrySet().iterator();

while (iterator.hasNext()) {

Map.Entry<Integer, String> entry = iterator.next();

System.out.print(entry.getKey());

System.out.print(entry.getValue());

BFS和DFS

广度优先搜索算法（Breadth-First-Search，缩写为 BFS），是一种利用队列实现的搜索算法。简单来说，其搜索过程和 “湖面丢进一块石头激起层层涟漪” 类似。把符合条件的逐渐加到队列的后面，有点类似层序遍历的感觉。

深度优先搜索算法（Depth-First-Search，缩写为 DFS），是一种利用递归实现的搜索算法。简单来说，其搜索过程和 “不撞南墙不回头” 类似。一直往下走直到找不到符合条件的下一步为止。如果不用递归的话也可以用栈实现

把一个有向无环图转换为线性的排序叫做拓扑排序

有向图有入度和出度的概念，可以根据入度和出度来做一些方向上以及顺序上的判定。

200、岛屿数量

题目说明

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围

解题思路1：DFS

岛屿数量用res进行统计

对整个gird数组进行遍历，当遇到“陆地”（grid[i][j]==1）时，把他置为0，岛屿数量加一。并对其上下左右进行扩散直到这一块陆地全部被置为0。当grid数组遍历完时res即为岛屿的数量。

public void dfs(char[][] grid, int row, int col) {
    if(row < 0 || row >= grid.length || col < 0 || col >= grid[0].length || grid[row][col] == '0') {
        return;
    }
    grid[row][col] = '0';
    dfs(grid, row + 1, col);
    dfs(grid, row - 1, col);
    dfs(grid, row, col + 1);
    dfs(grid, row, col - 1);
}

解题思路2：BFS

虽然这个地方说是BFS，但是个人感觉还是DFS的思路，虽然写出来的形式跟BFS的形式是一样的。

同样对grid进行遍历。设置一个队列neighbors，用来记录岛屿，并且对其上下左右位置不断进行展开加入队列，并把这些节点置0。neighbors存储岛屿的坐标，坐标可以用二维数组的形式存储，也可以用row * length + col的形式存储。直到这一块岛屿结束之后（neighbors.isEmpty()），则退出遍历。

Queue<Integer> neighbors = new LinkedList<Integer>();
neighbors.offer(i * length + j);
while (!neighbors.isEmpty()) {
    int id = neighbors.poll();
    int row = id / length;
    int col = id % length;
    if (row - 1 >= 0 && grid[row - 1][col] == '1') {
        grid[row - 1][col] = '0';
        neighbors.offer((row - 1) * length + col);
    }
    if (col - 1 >= 0 && grid[row][col - 1] == '1') {
        grid[row][col - 1] = '0';
        neighbors.offer(row * length + col - 1);
    }
    if (row + 1 <= width - 1 && grid[row + 1][col] == '1') {
        grid[row + 1][col] = '0';
        neighbors.offer((row + 1) * length + col);
    }
    if (col + 1 <= length - 1 && grid[row][col + 1] == '1') {
        grid[row][col + 1] = '0';
        neighbors.offer(row * length + col + 1);
    }

994、腐烂的橘子

题目说明

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。
每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

解题思路：BFS

因为本题需要求没有新鲜橘子的最小分钟数。如果用dfs去求解的话，对每一个板块进行dfs都会获得一个时间，最终的结果（如果都会腐烂）则是最大的那个时间。这样不是很方便，所以本题采用BFS方法一层一层的遍历，用队列的方式来控制层数（有点类似二叉树的层序遍历那样），每一层代表一个

首先对grid进行遍历，目的是统计新鲜橘子的数量以及确定烂橘子的位置，此时时间为0分钟。依据类似层次遍历的方法，每次最多只会往上下左右的位置烂，每分钟只有原先队列中已经有的橘子能去扩散，直到队列中没有橘子可以扩散烂橘子为止。每当可以让一个橘子变烂时就让新橘子数量-1，最终结果依据新橘子数量是否为0去判定。

队列用于存储烂橘子的坐标，可以是一个数组，也可以是row * lenght + col。

while (goodOrange > 0 && !queue.isEmpty()) {
    int size = queue.size();
    time++;
    for (int i = 0; i < size; i++) {
        int id = queue.poll();
        int row = id / length;
        int col = id % length;
        if (row - 1 >= 0 && grid[row - 1][col] == 1) {
            goodOrange--;
            grid[row - 1][col] = 2;
            queue.offer((row - 1) * length + col);
        }
        if (row + 1 < width && grid[row + 1][col] == 1) {
            goodOrange--;
            grid[row + 1][col] = 2;
            queue.offer((row + 1) * length + col);
        }
        if (col - 1 >= 0 && grid[row][col - 1] == 1) {
            goodOrange--;
            grid[row][col - 1] = 2;
            queue.offer(row * length + col - 1);
        }
        if (col + 1 < length && grid[row][col + 1] == 1) {
            goodOrange--;
            grid[row][col + 1] = 2;
            queue.offer(row * length + col + 1);
        }
    }
}

207、课程表

题目说明

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

注意，一门课程可能有多门先修课程

解题思路1：BFS

采用两个map表分别记录以下信息：map1记录某一课程的当前先修课程数量，map2记录依赖于某一课程的课程（可能有多个，用list存储）（相当于一个邻接表），通过对prerequisites遍历之后对这两个map进行更新

用队列来存储可以直接修的课程（当前课程无先修课程或先修课程已经修完），直到队列为空，即无法再修新的课程了。初始化队列则对map1进行遍历，如果先修课程数量为0即可加入队列。最后对map1进行遍历，如果仍有课程的先修课程数量不为0则说明无法修完，反之说明所有课程都可以顺利修完。

解题思路2：DFS

此处DFS应用到了一个将有向无环图转换为线性的排序，也就是拓扑排序的思路，在此题中的体现可以理解为，不断的从任一一个节点进行DFS，只要他后面的课程不会到他自己（即不会成环），说明图中不存在环，一定可以将每个节点都遍历完（在不依赖他的子节点的情况下）

代码如下

visited = new int[numCourses]; // 用于存储节点的状态，0为未访问，1未访问中，2为访问过了
edges = new ArrayList<List<Integer>>();
for (int i = 0; i < numCourses; i++) {
    edges.add(new ArrayList<Integer>()); 
    // 记录依赖于该课程的后续课程（该课程为他们的先修课程）
}
for (int[] prerequisite : prerequisites) {
   edges.get(prerequisite[1]).add(prerequisite[0]);
}
for (int i = 0; i < numCourses && tag; i++) {
    if(visited[i] == 0) { // 为访问过则开始访问
        dfs(i);
    }
}

public void dfs(int u) {
    	//首先将当前节点置为访问中的状态
        visited[u] = 1; 
    	//对依赖该节点的后续节点依次进行访问
        List<Integer> edge = edges.get(u);
        for (Integer v : edge) {
            //还没访问过就访问
            if (visited[v] == 0) {
                dfs(v);
                if (!tag) {
                    // 如果成环则后面不用遍历了
                    return;
                }
                // 如果该节点正在被访问，说明图中成环
            } else if (visited[v] == 1) {
                //tag标记是否有环
                tag = false;
                return;
            }
        }
    	// 该节点及其后续路径访问结束，没有问题
        visited[u] = 2;
    }

208、实现 Trie (前缀树)

题目说明

请你实现 Trie 类：

1. Trie() 初始化前缀树对象。
2. void insert(String word) 向前缀树中插入字符串 word 。
3. boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
4. boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

解题思路

首先要知道前缀树是个什么东西（如下）

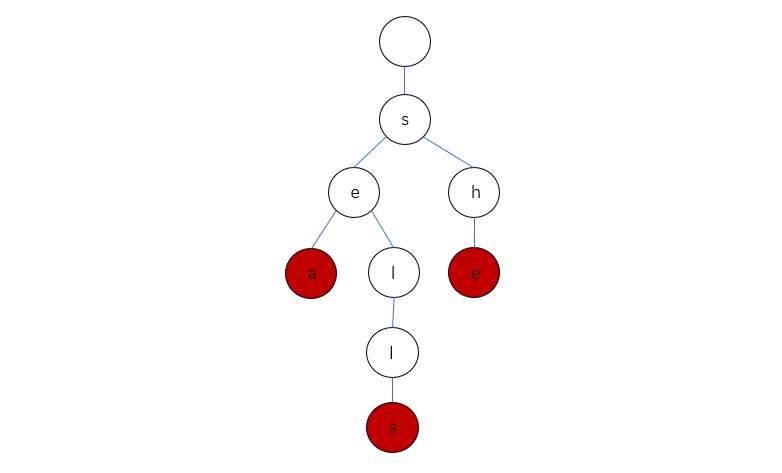
包含三个单词 "sea","sells","she" 的 Trie 会长啥样呢？

可以理解为是一个多叉树，每个字母对应一个节点。由于题目限定该前缀树只由小写字母组成，所以我们不用List来存储可能动态扩大的字母，因为只有26个，那么意味该节点最多只有26个节点，那么做一个包含26个节点的数组即可，如果某个字母被用到，对对应的index直接new一个新节点即可。且我们需要标记单词的结尾，所以我们额外需要一个Boolean型变量来判定该节点是否为单词的末尾。

因此，前缀树初始化只需有一个数组和一个标记即可

public Trie() {
    children = new Trie[26];
    isEnd = false;
}

插入则对单词的每一个字母作为一个节点插入到后面，如果节点存在则往后走，不存在创建一个新的。当到单词末尾（最后一个字母时）要注意把isEnd变量修改为true，确实到单词的末尾了。

public void insert(String word) {
    Trie node = this;
    for (int i = 0; i < word.length(); i++) {
        char ch = word.charAt(i);
        int index = ch - 'a';
        if (node.children[index] == null) {
            node.children[index] = new Trie();
        }
        node = node.children[index];
    }
    node.isEnd = true;
}

判定是否包含前缀或者包含某个单词的区别只在于是否需要对isEnd进行判断，其余步骤都是一样的，从头节点顺下来一步一步往下走，不存在则返回false，存在则往下走。前缀如果可以走到前缀的末尾即可直接返回true，包含某单词则需要判定当前节点是否是末尾if(isEnd)即可