Data structure and algorithm-Two
- B树

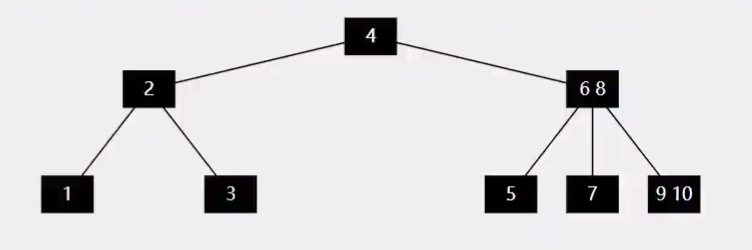

-

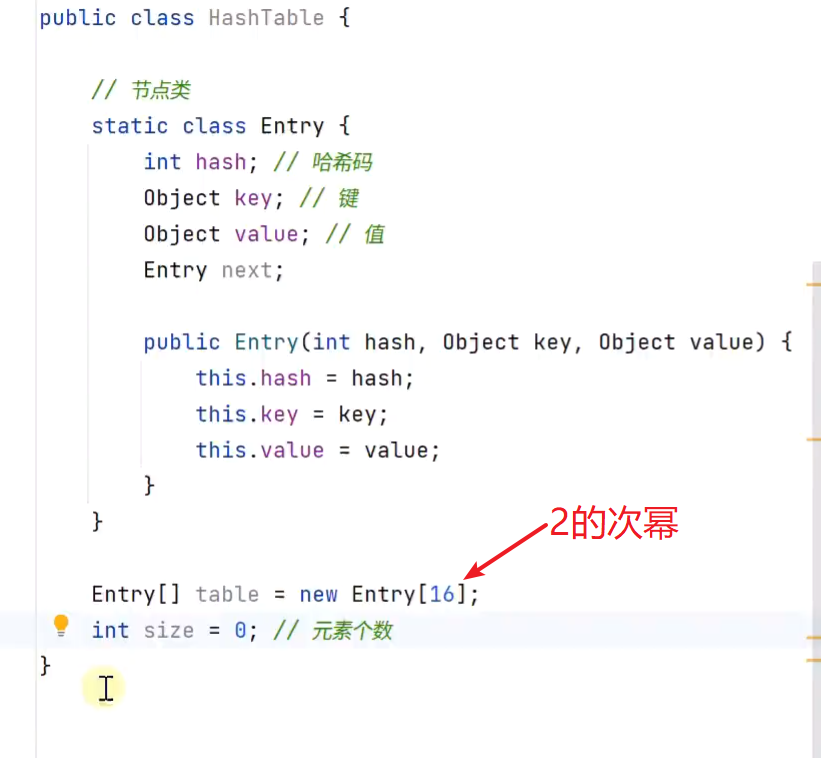


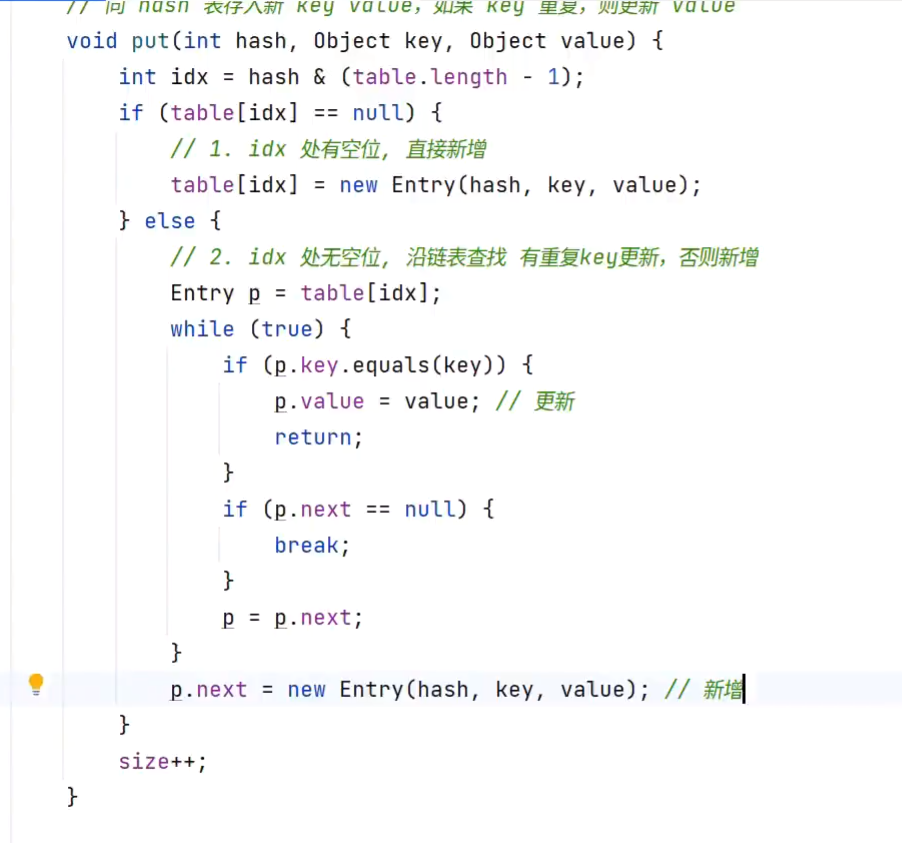
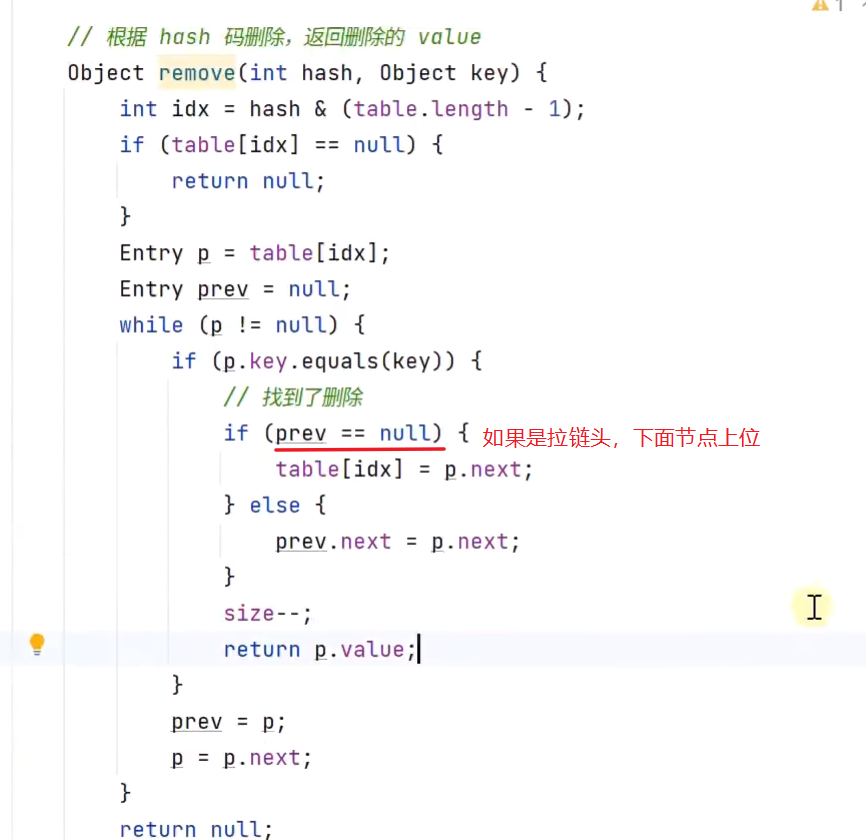
扩容



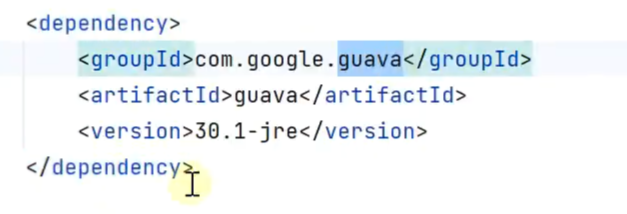


-
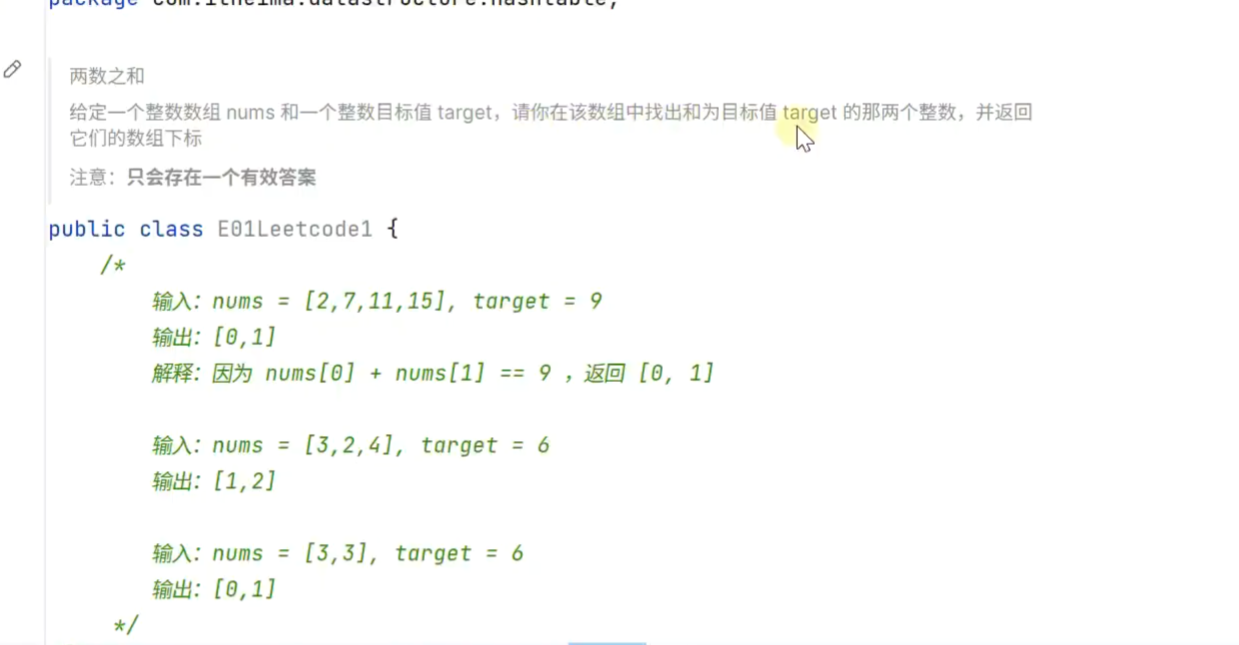
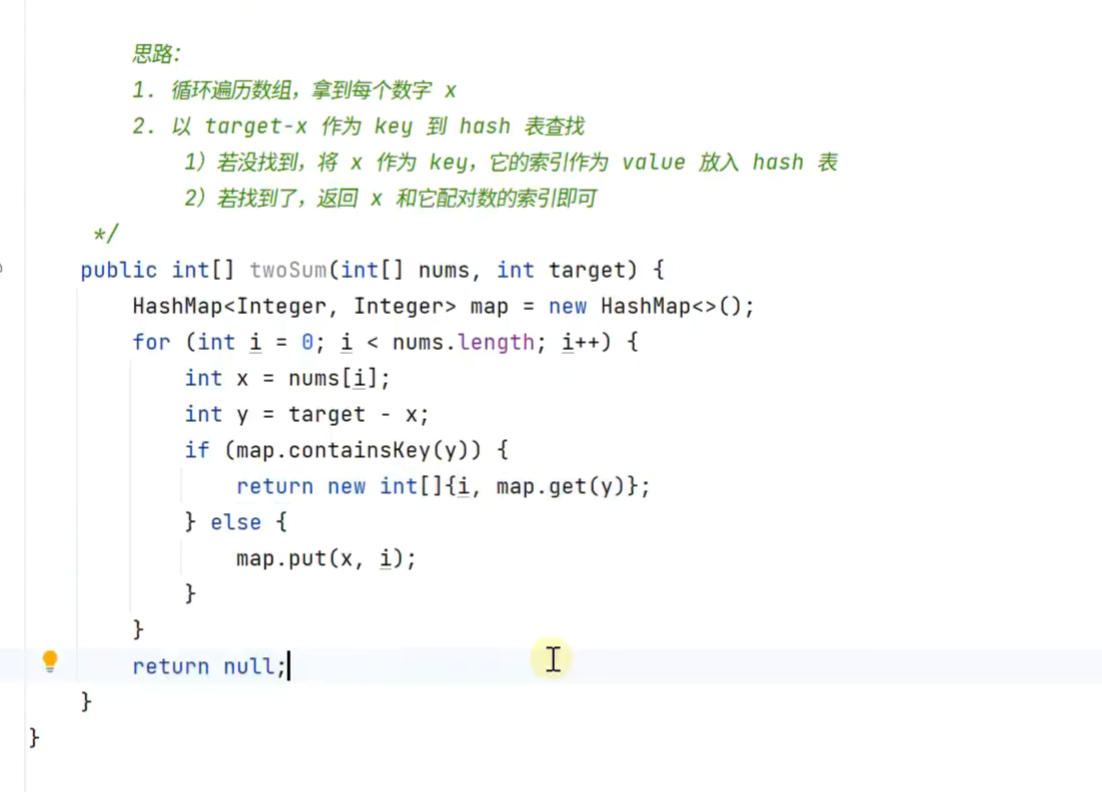
找出不含重复字符的最长字串的长度
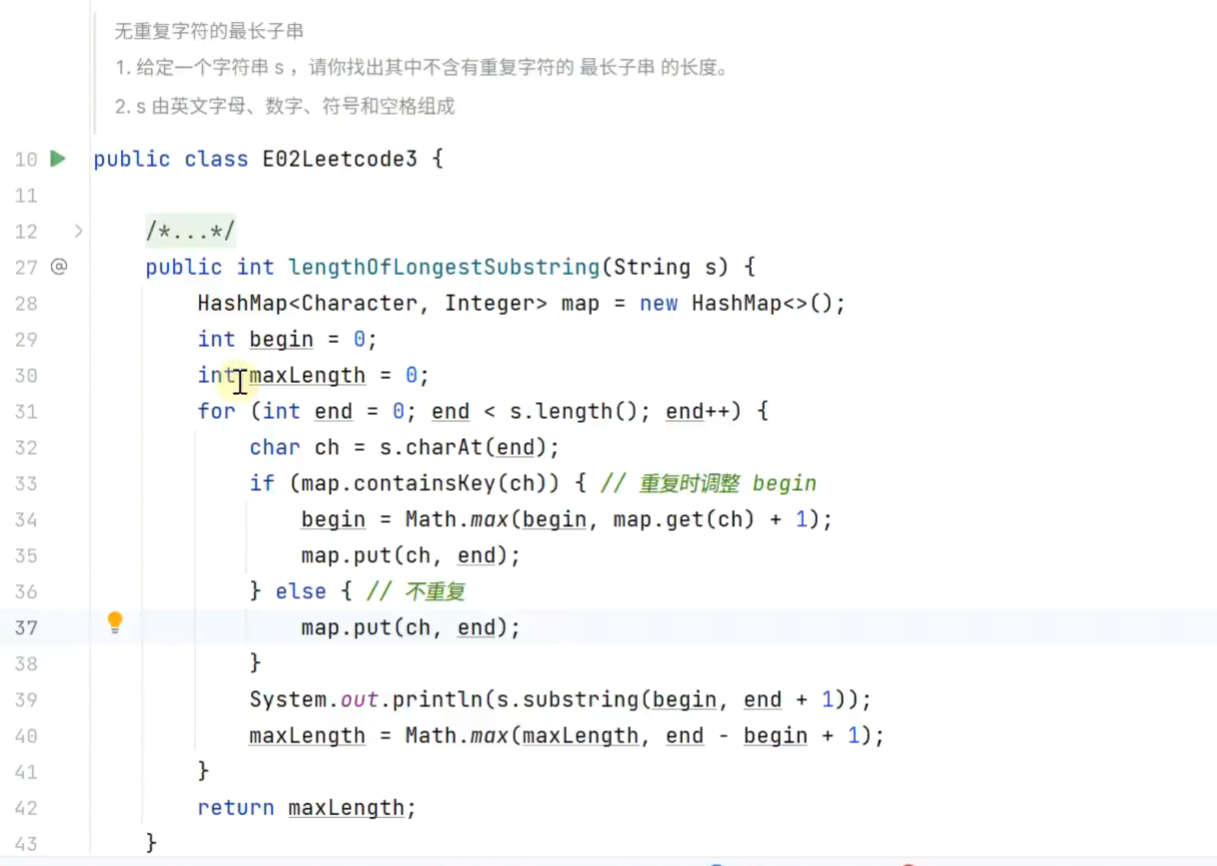
-
字母异位词分组
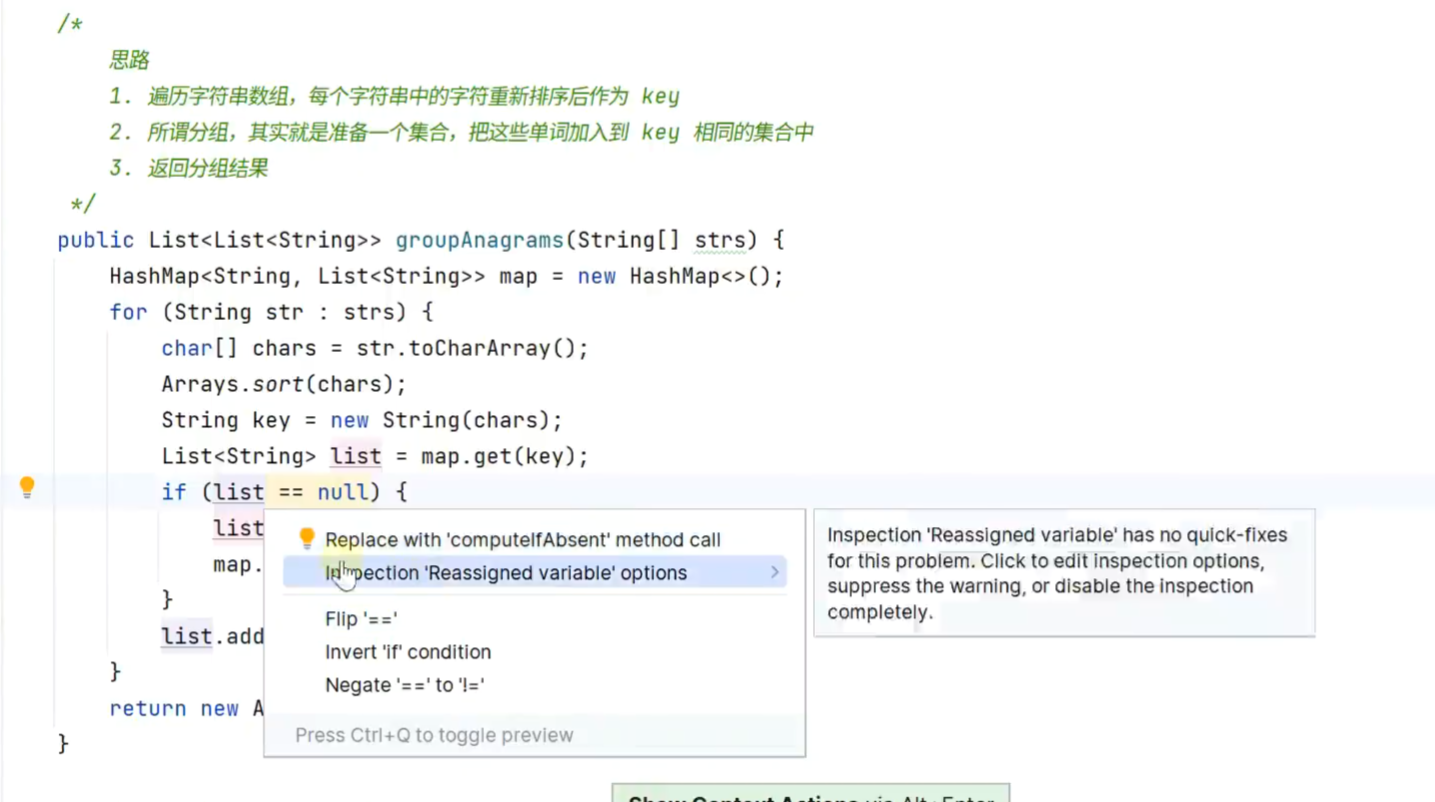

优化
用一个长度26的整数数组来标识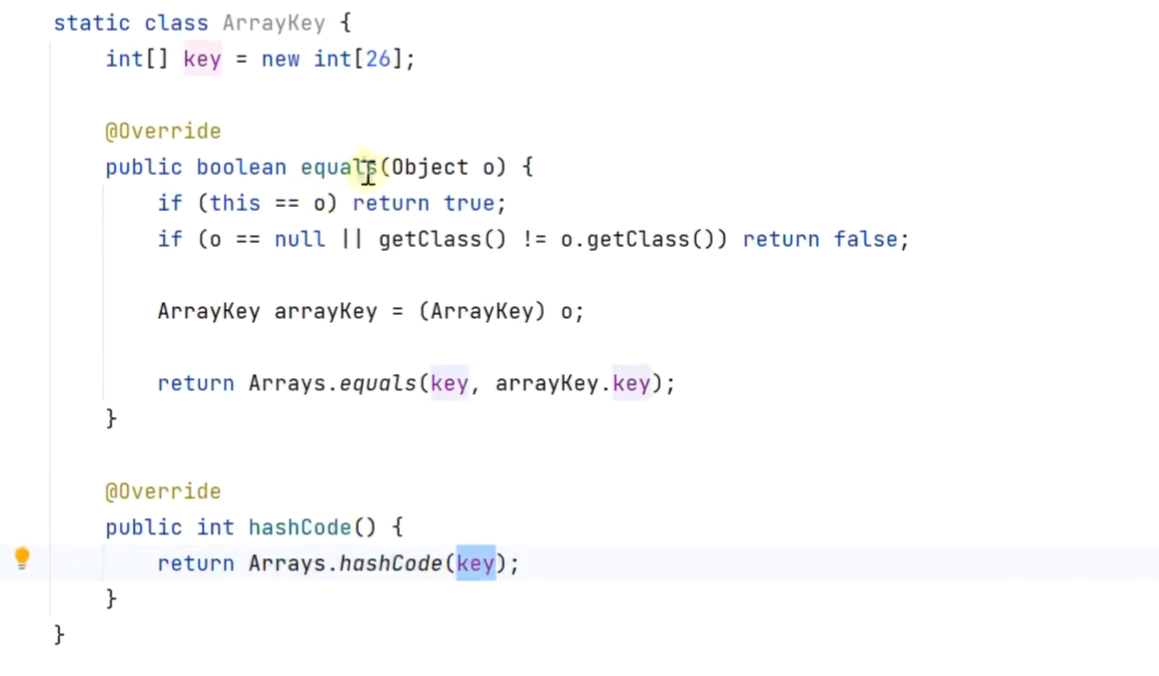
ArrayKey的构造方法

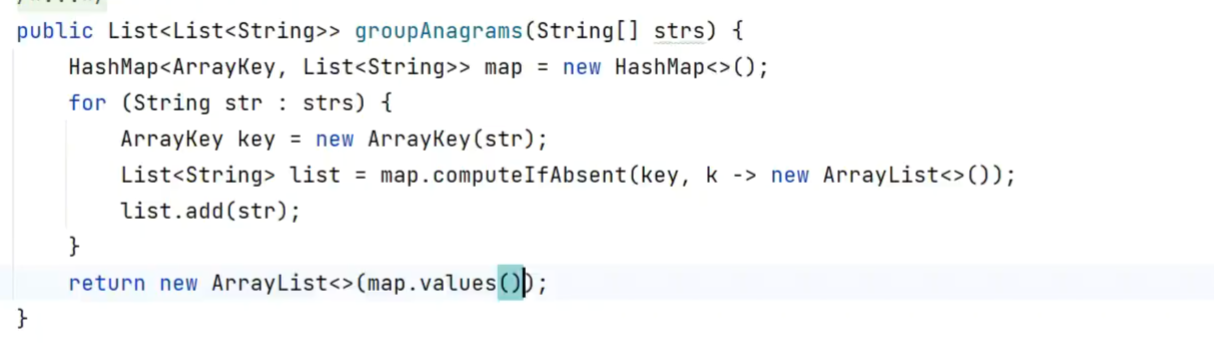
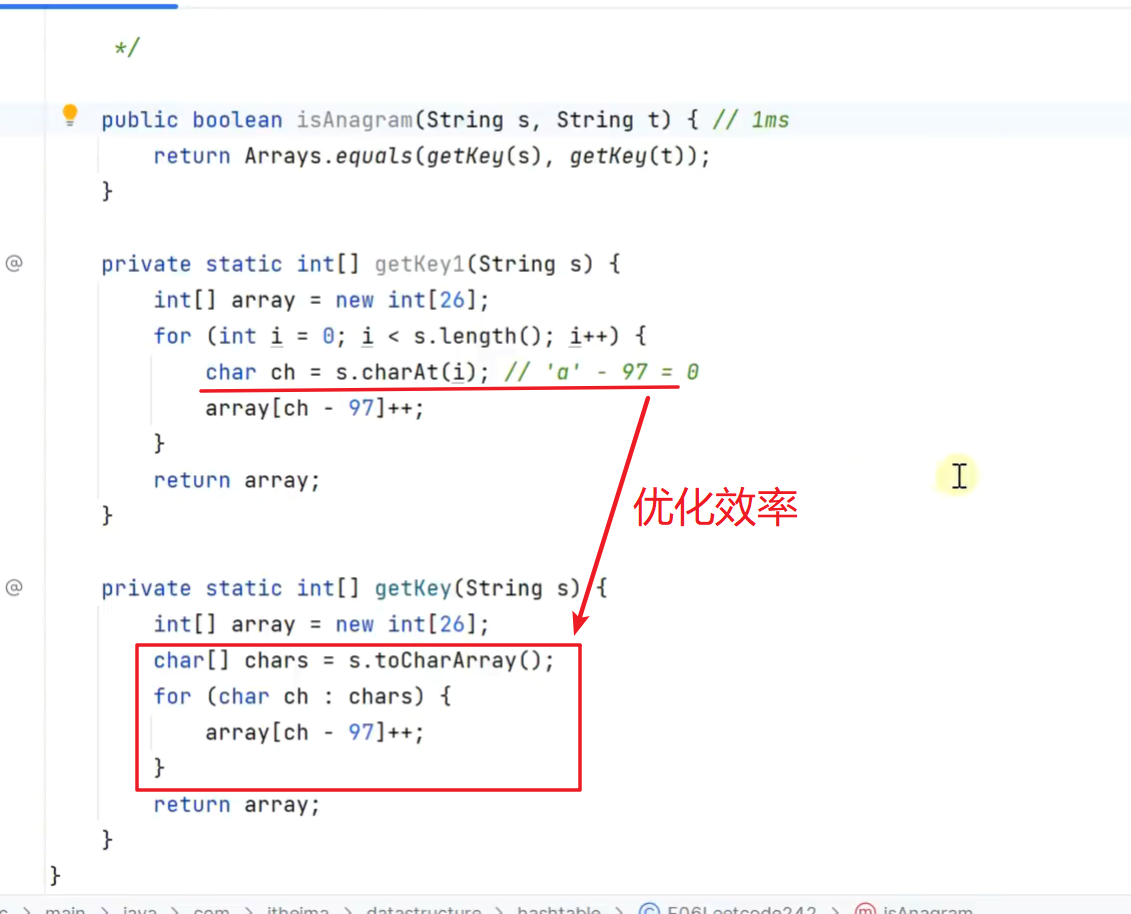
-
判断是否存在重复元素
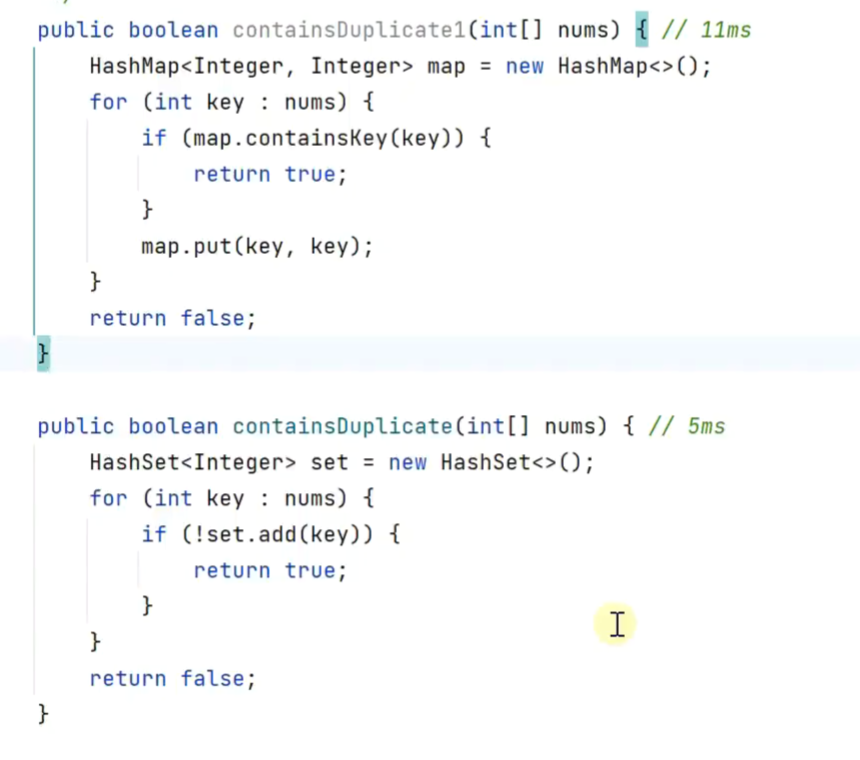
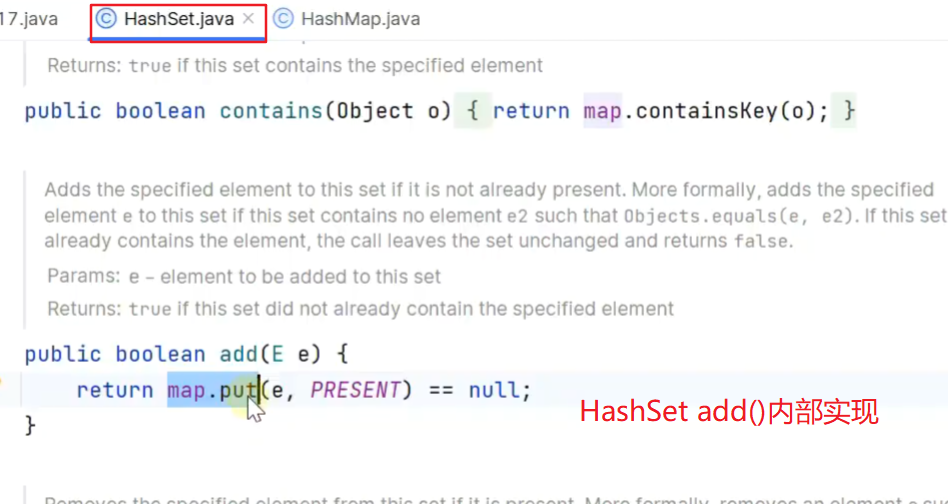
借鉴HashSet后的小优化版
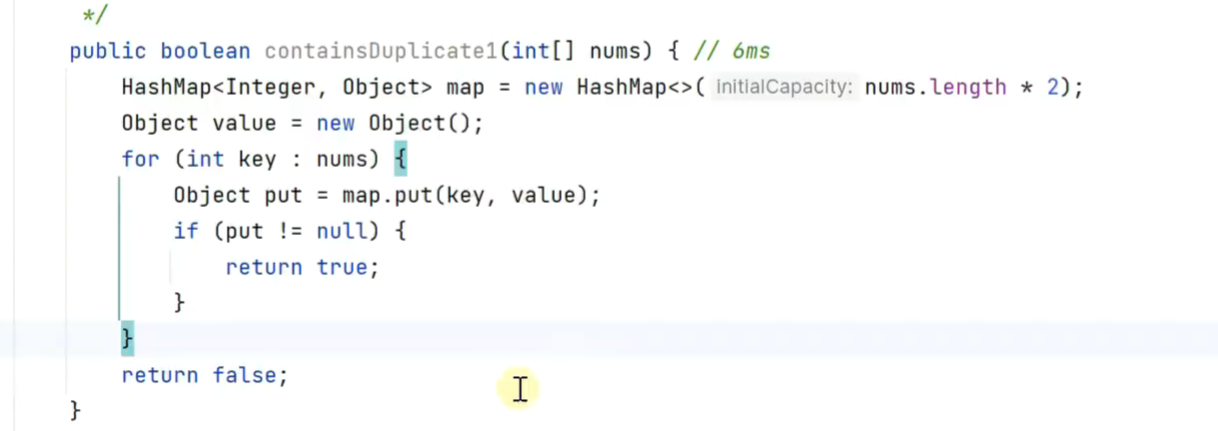
put 自带一个返回值,返回的是添加前原位置的元素,若原位置为空,则返回null
-

添加,若遇到重复元素,则在集合中删除,最后集合中只剩下没有重复的那个元素
效率不高
异或(异为1,同为0)
所有数字进行异或,相同的数字异或后为0,而0与原数字异或后的结果是数字本身
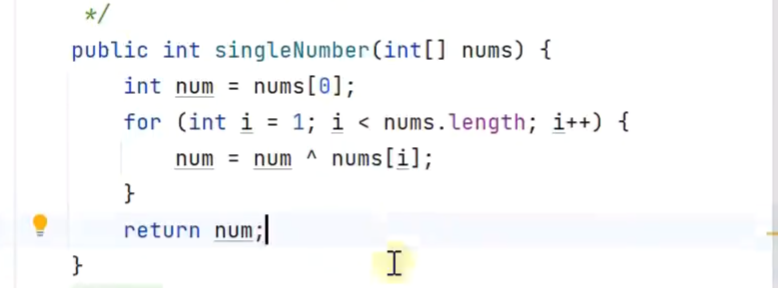
-
找出段落中出现次数最多的单词

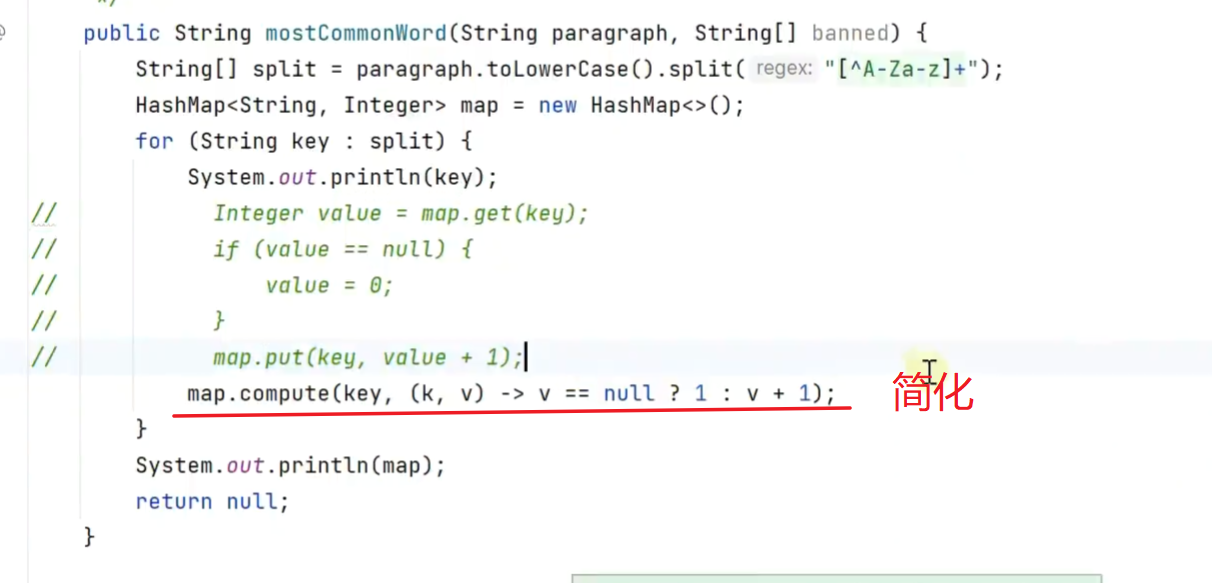
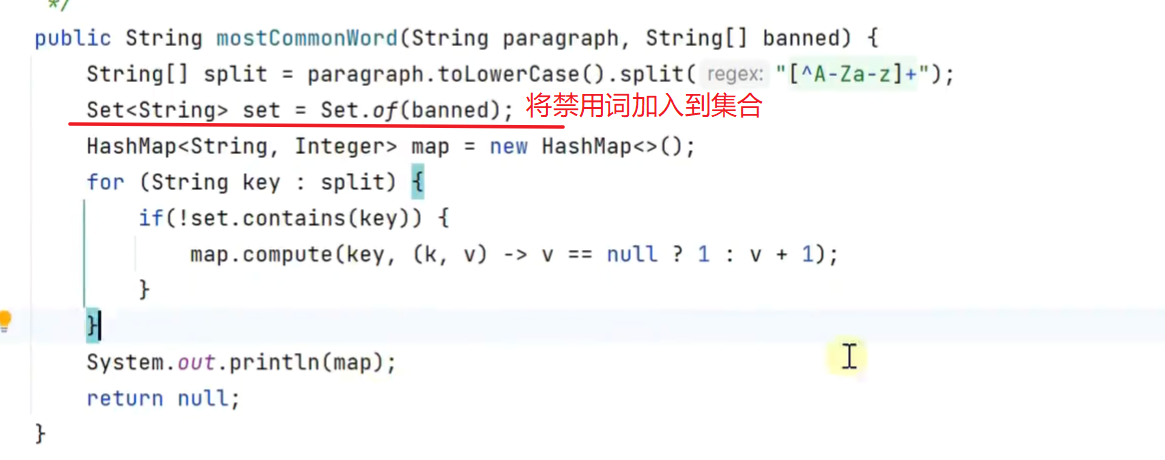
利用流找到最大频率


λ表达式缺点:运行效率不高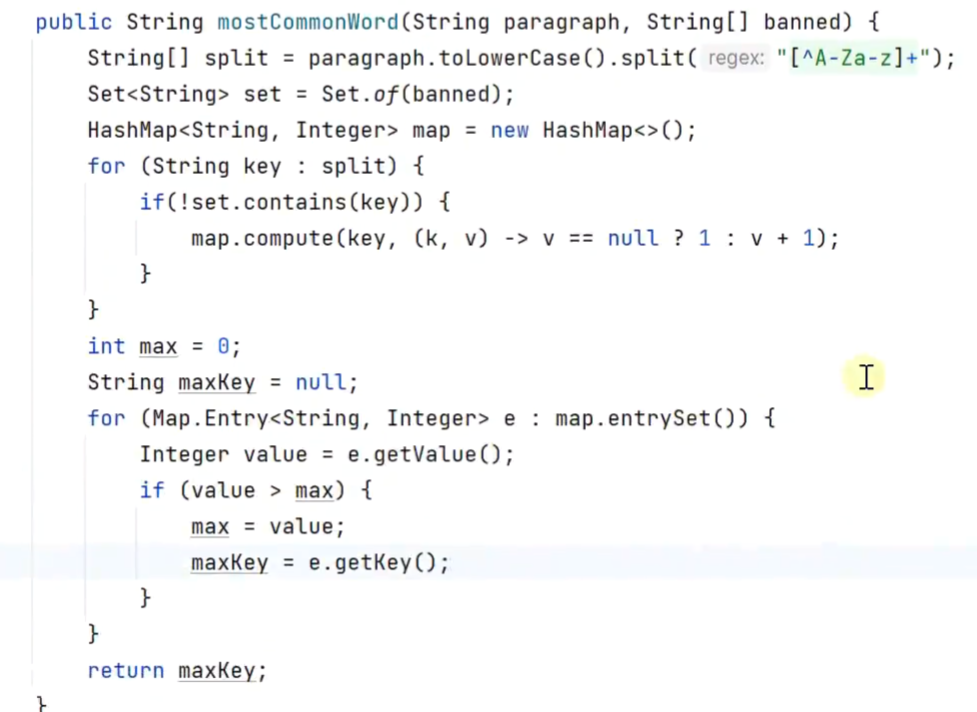
正则表达式效率也不高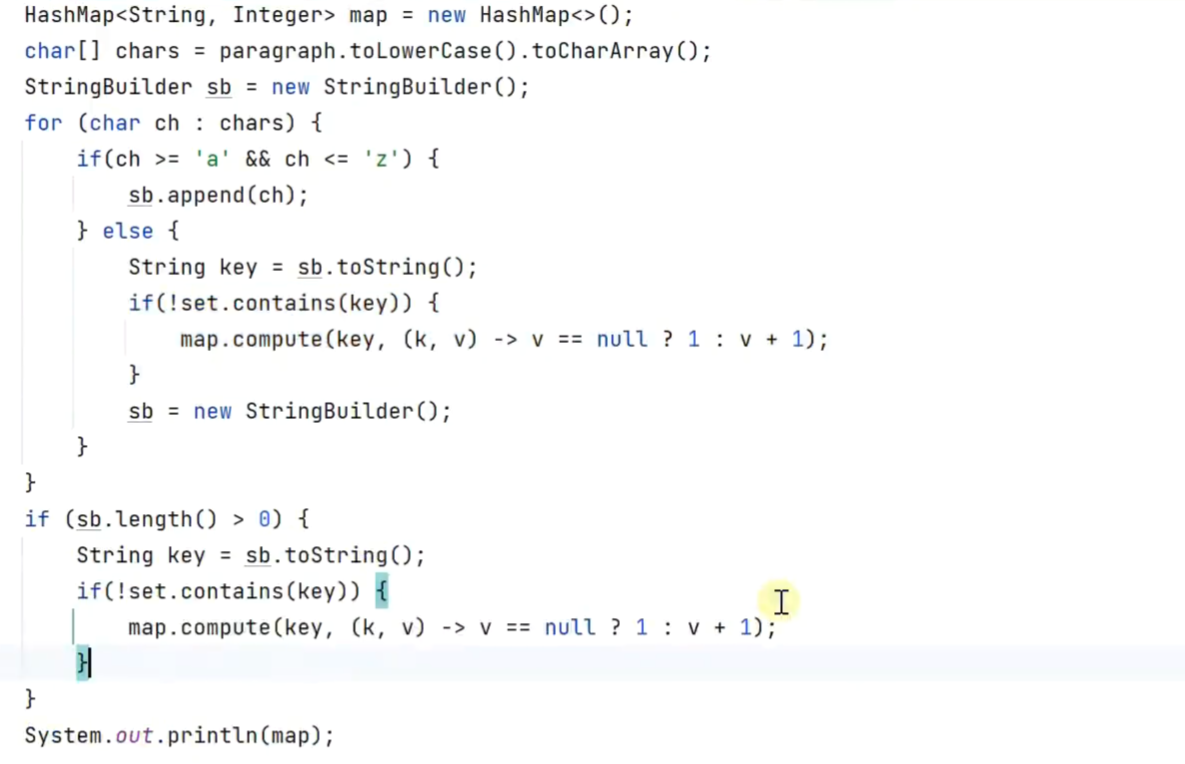
-
排序算法
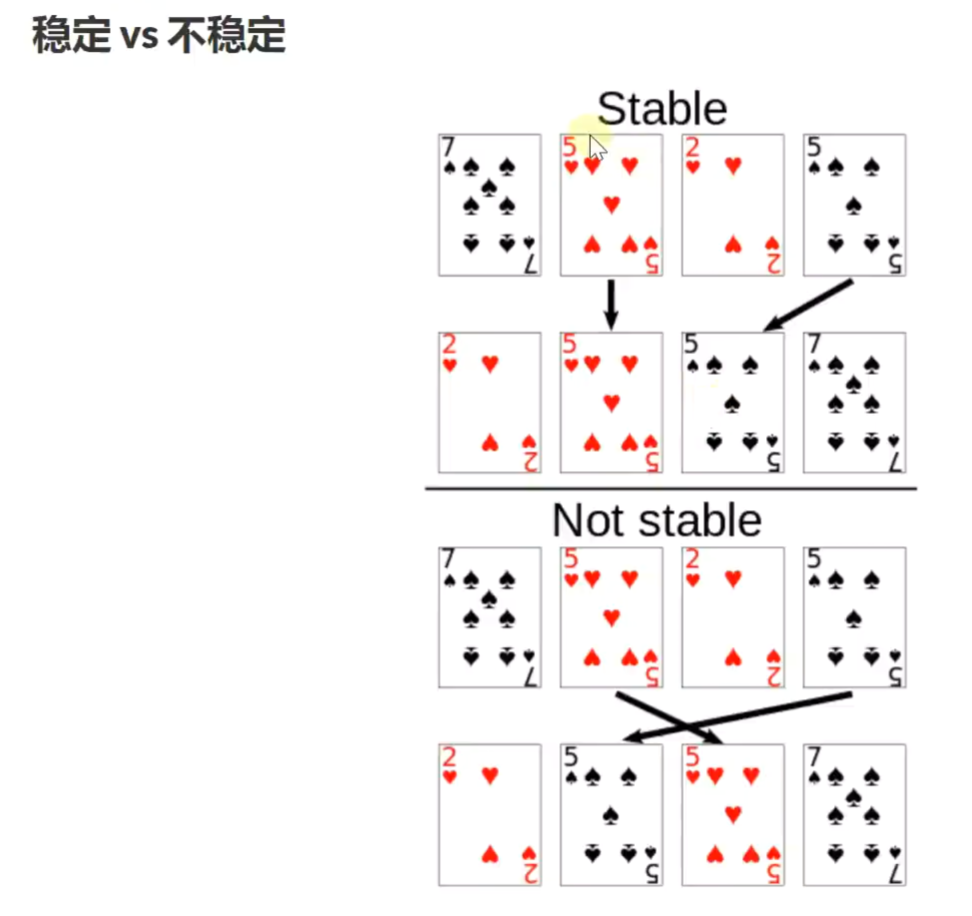
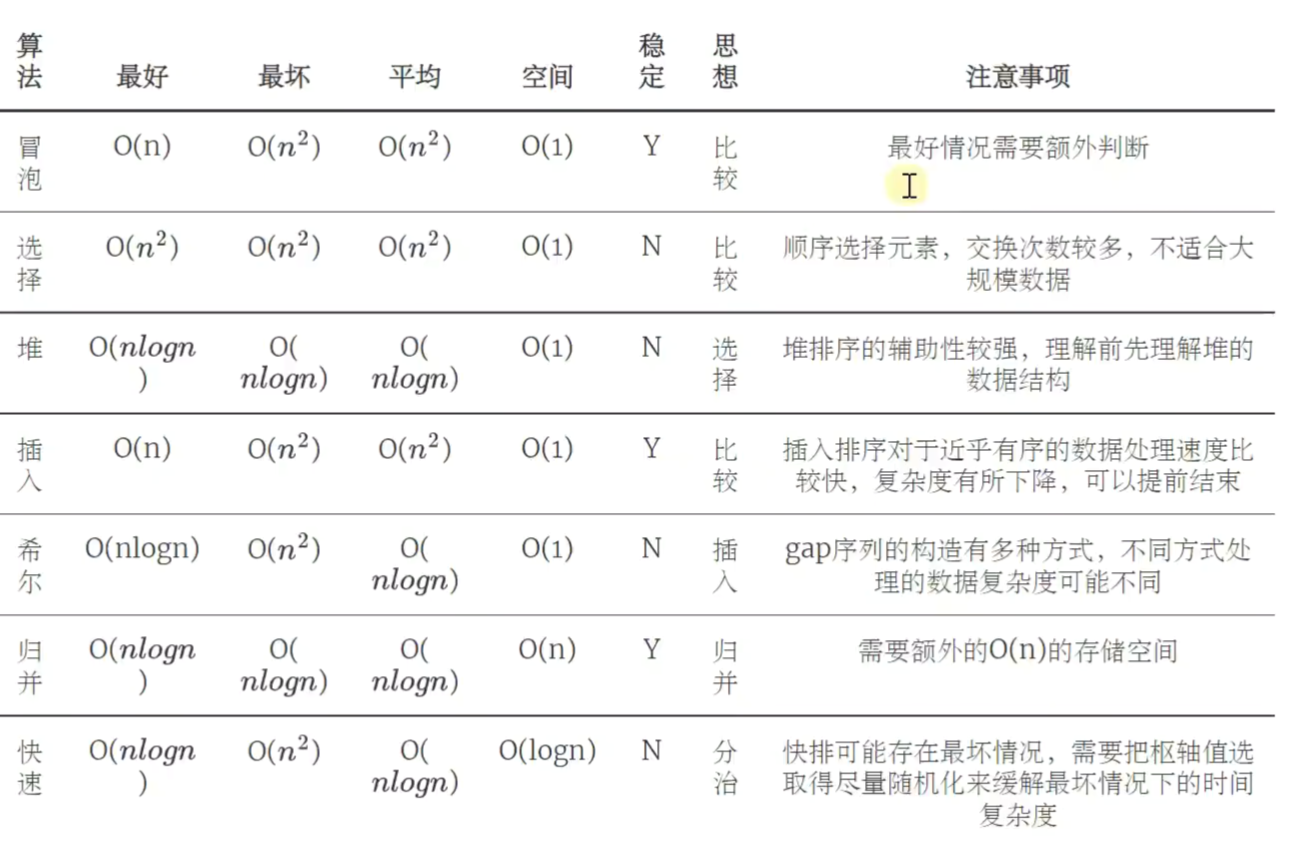


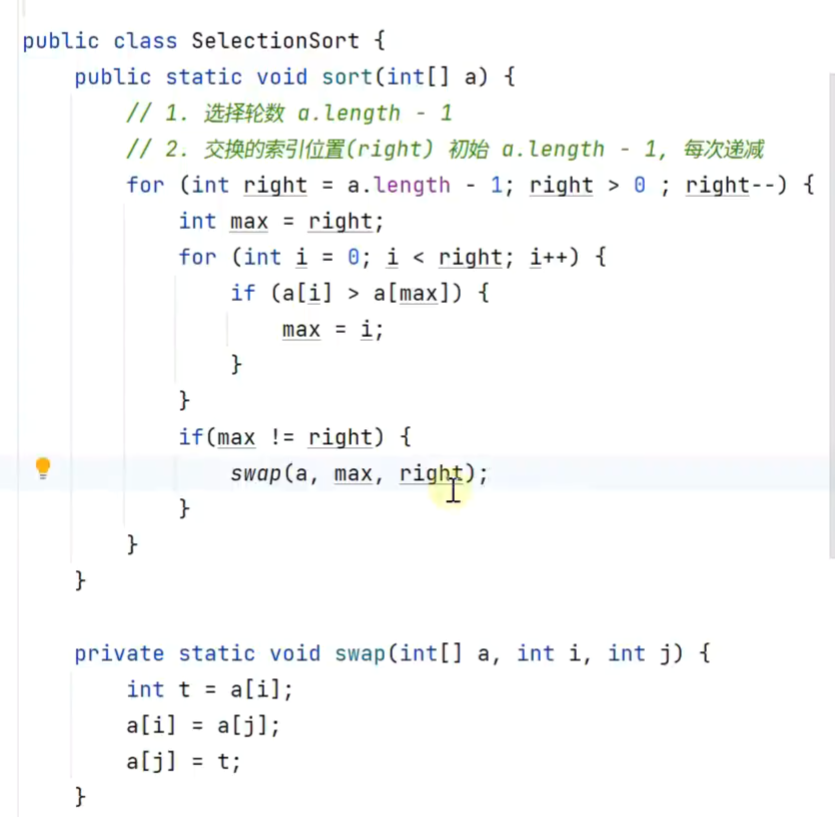
选择排序
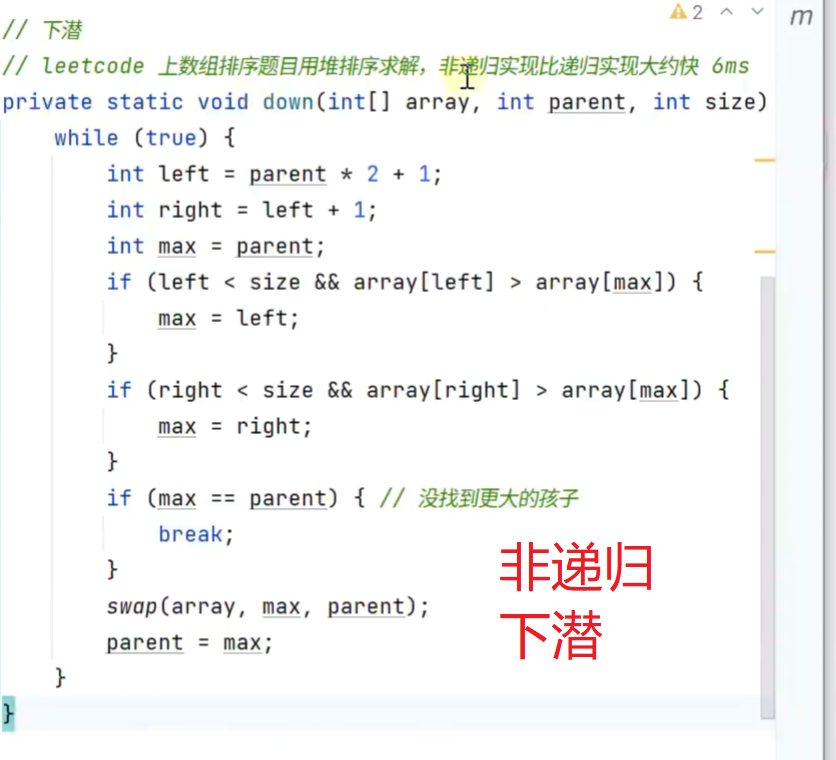
3.堆排序


4.插入排序

5.希尔排序
先分组,组内再插入排序
每次移动范围大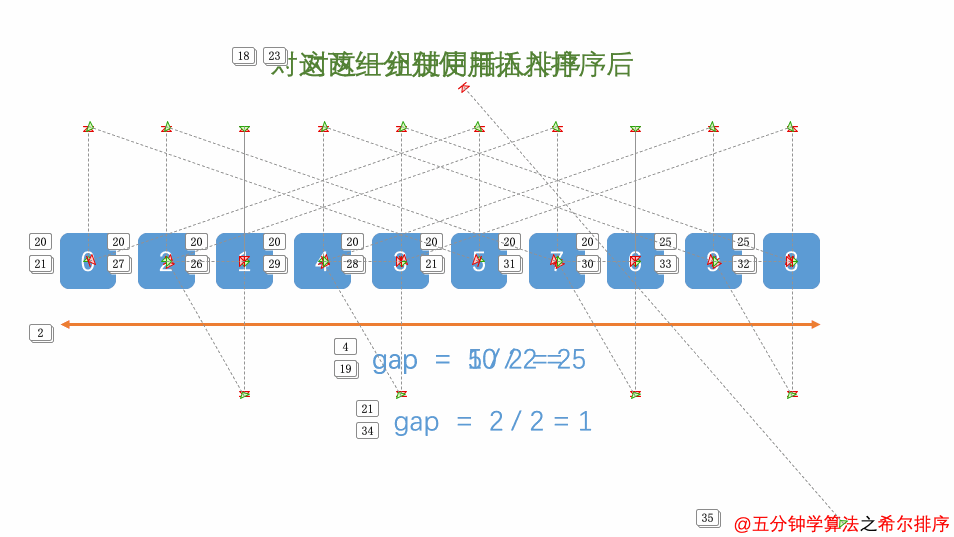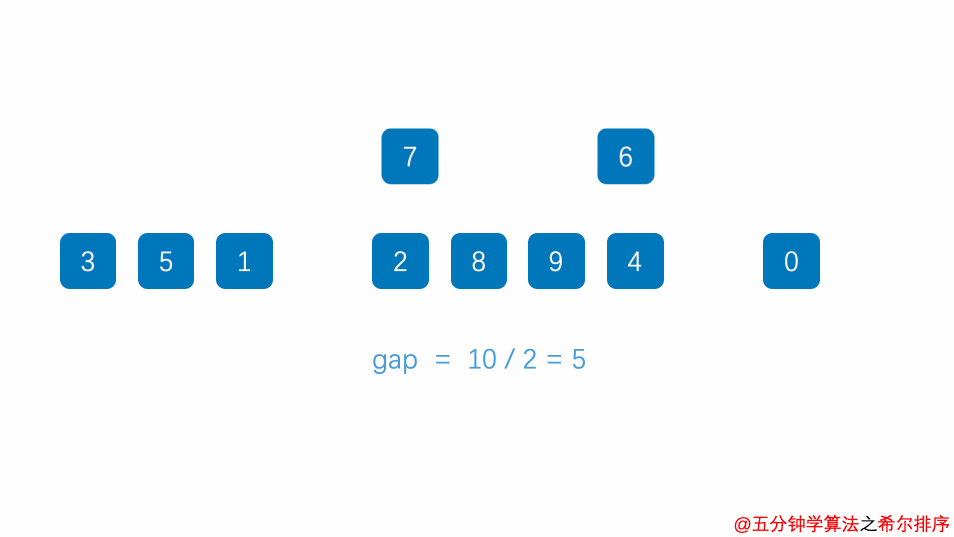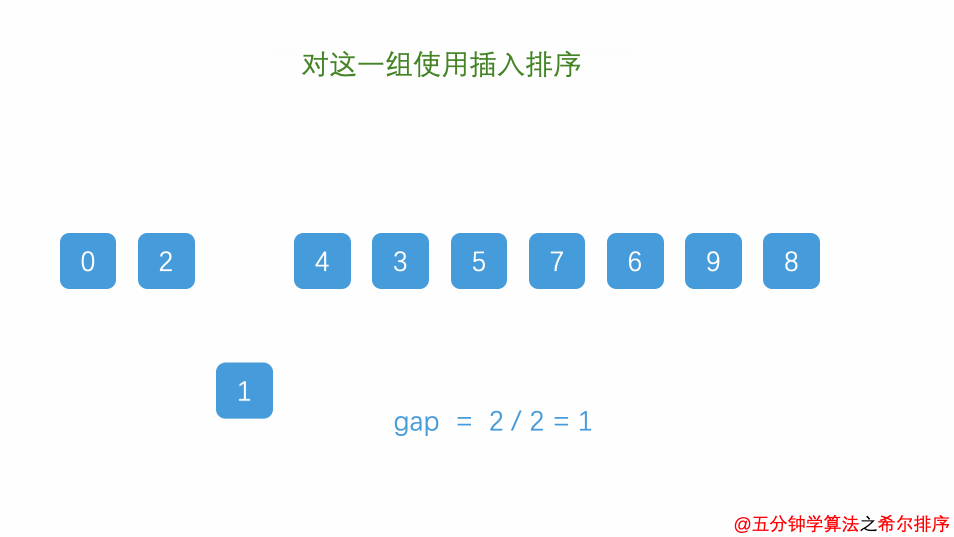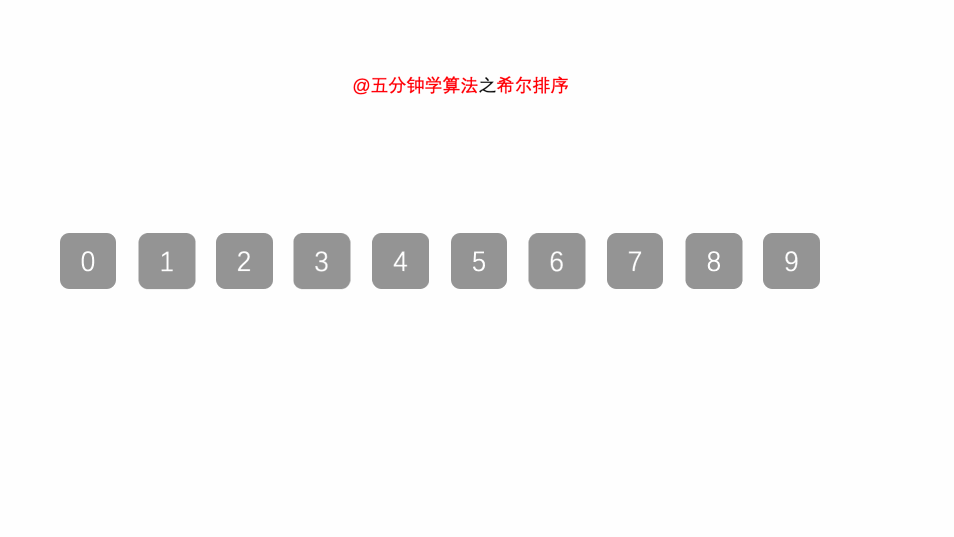

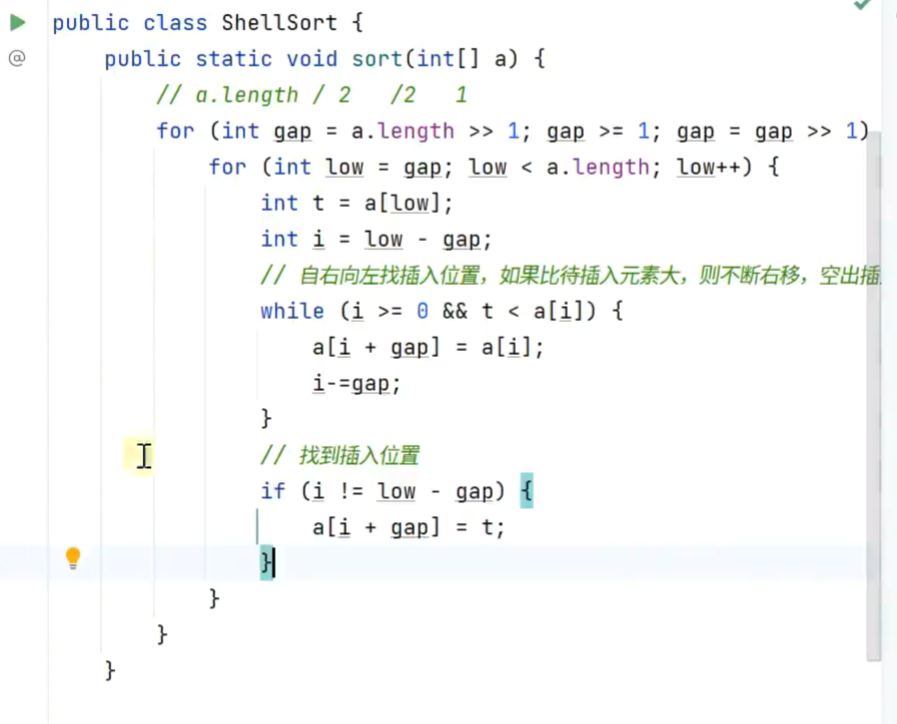
6.归并排序



递归 自上而下
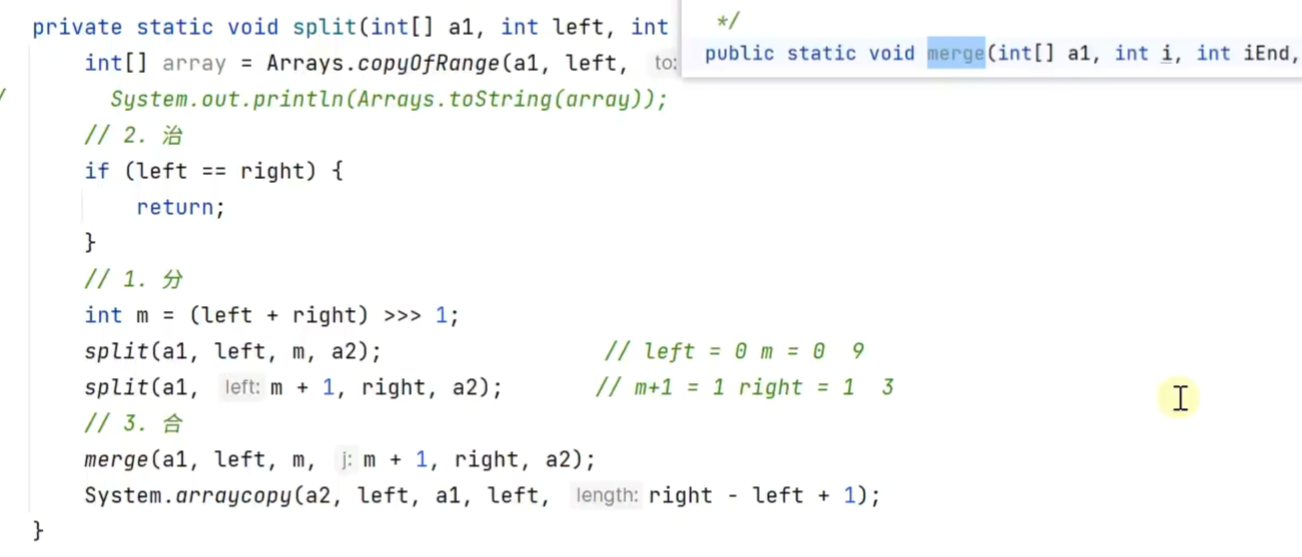
非递归 自下而上
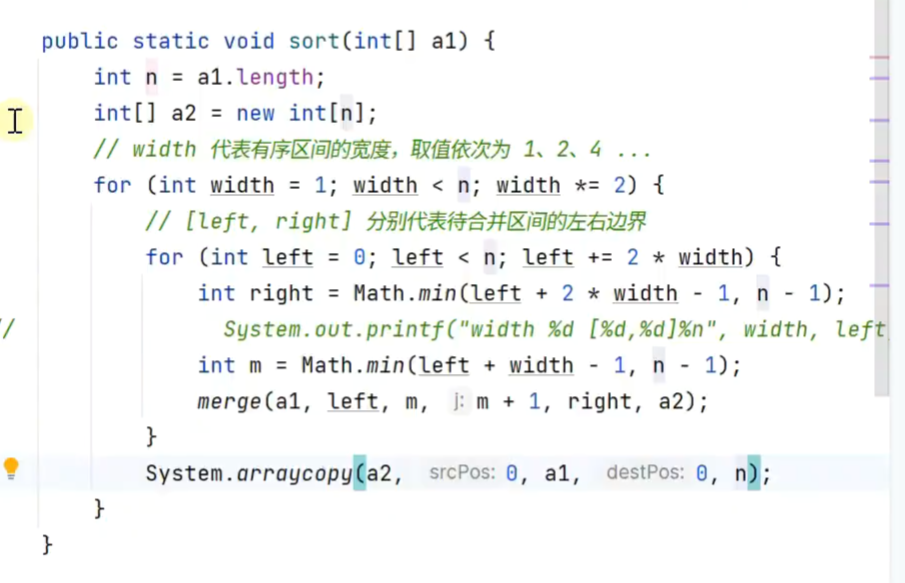
6.归 并+插入
归并 分到一定就调用插入排序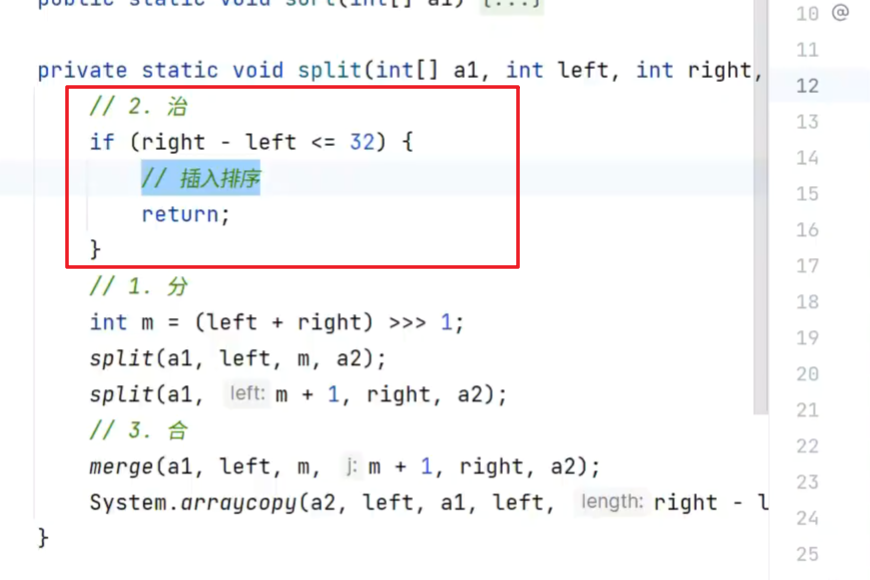

7.快速排序,基于比较的最快的排序算法
a.单边循环
遇到符合条件 则停,两个都遇到则交换位置

b.双边循环,双向奔赴

i找到与基准点相等的时候不停,故有重复元素时会偏右
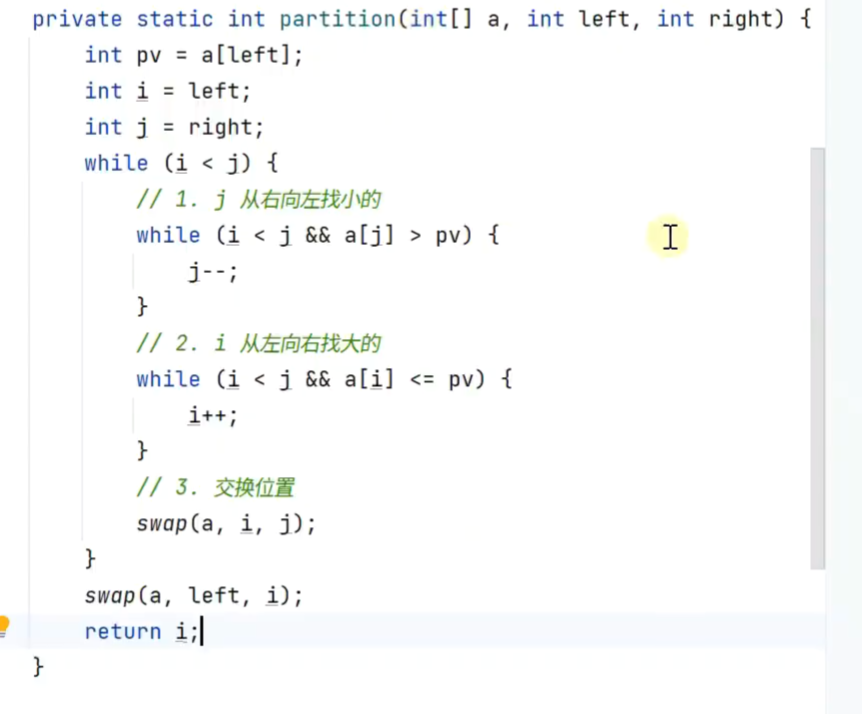
j i 代码顺序不能交换

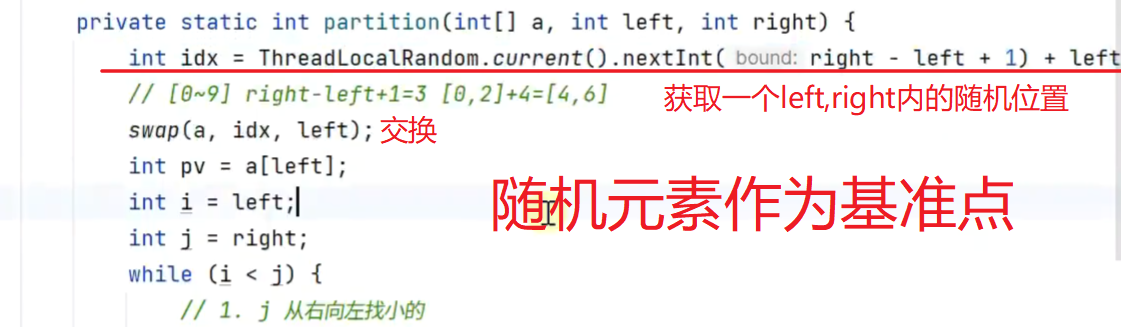
如何处理想等情况?不同:j为基准点索引最终值

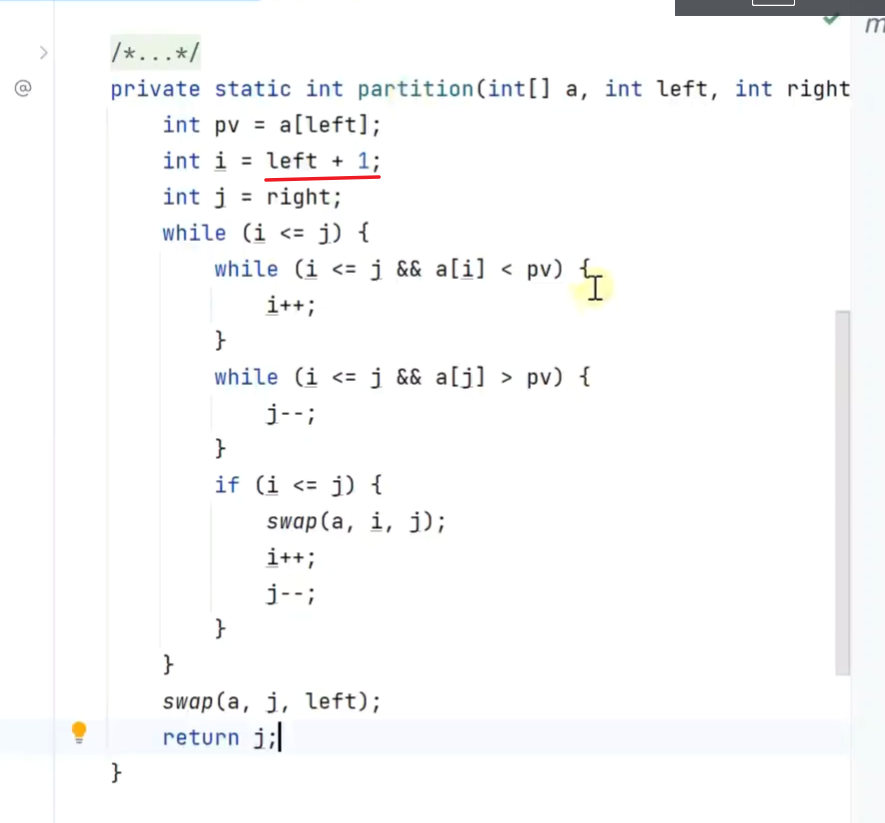
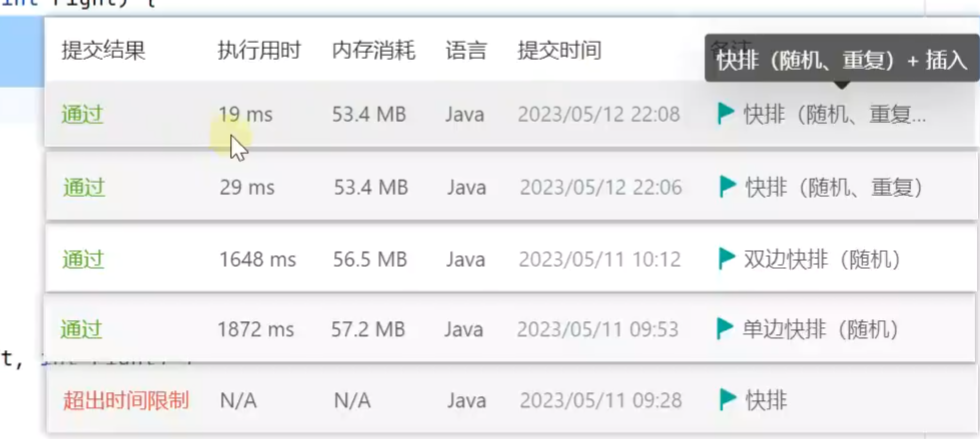
8.计数排序
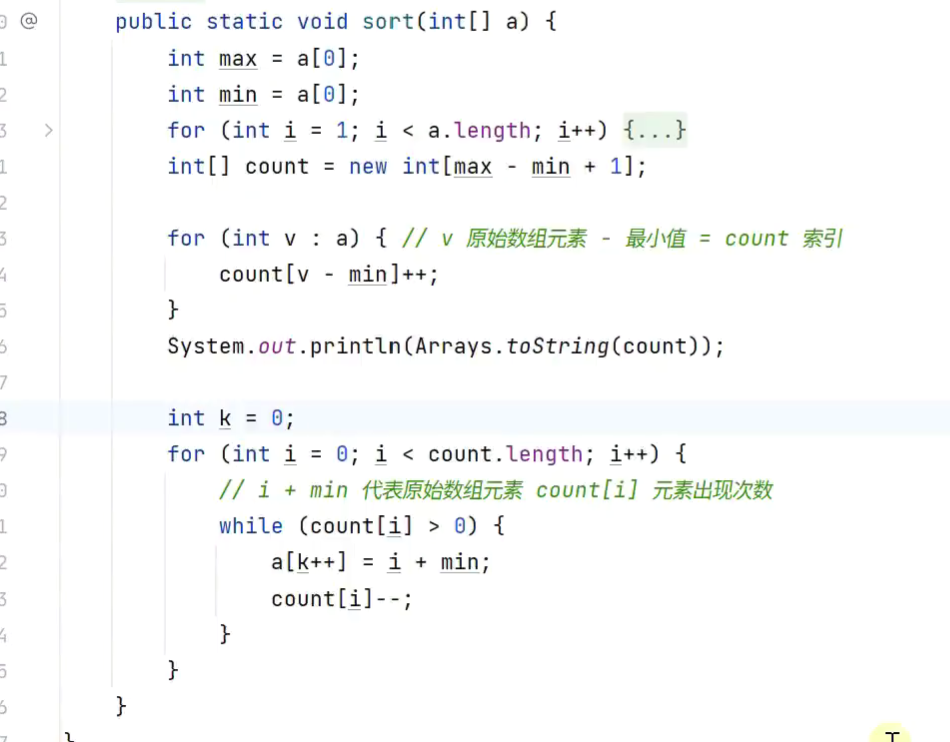
9.桶排序
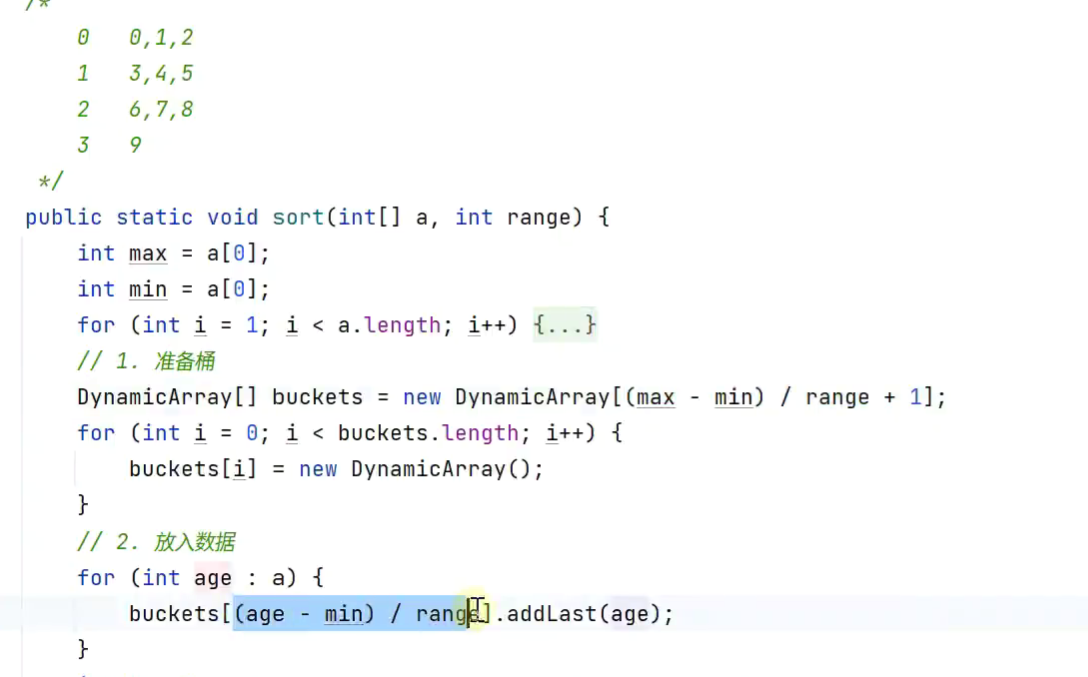
10.基数排序(按位排序)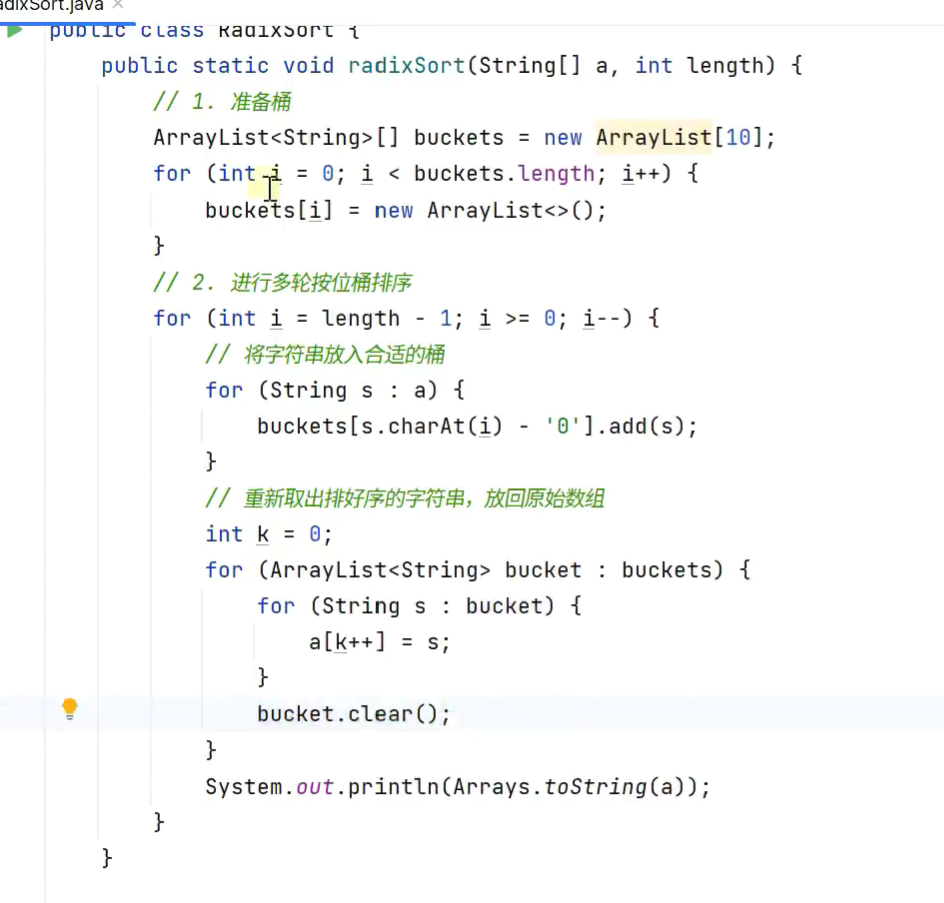
高位往低位排 msd
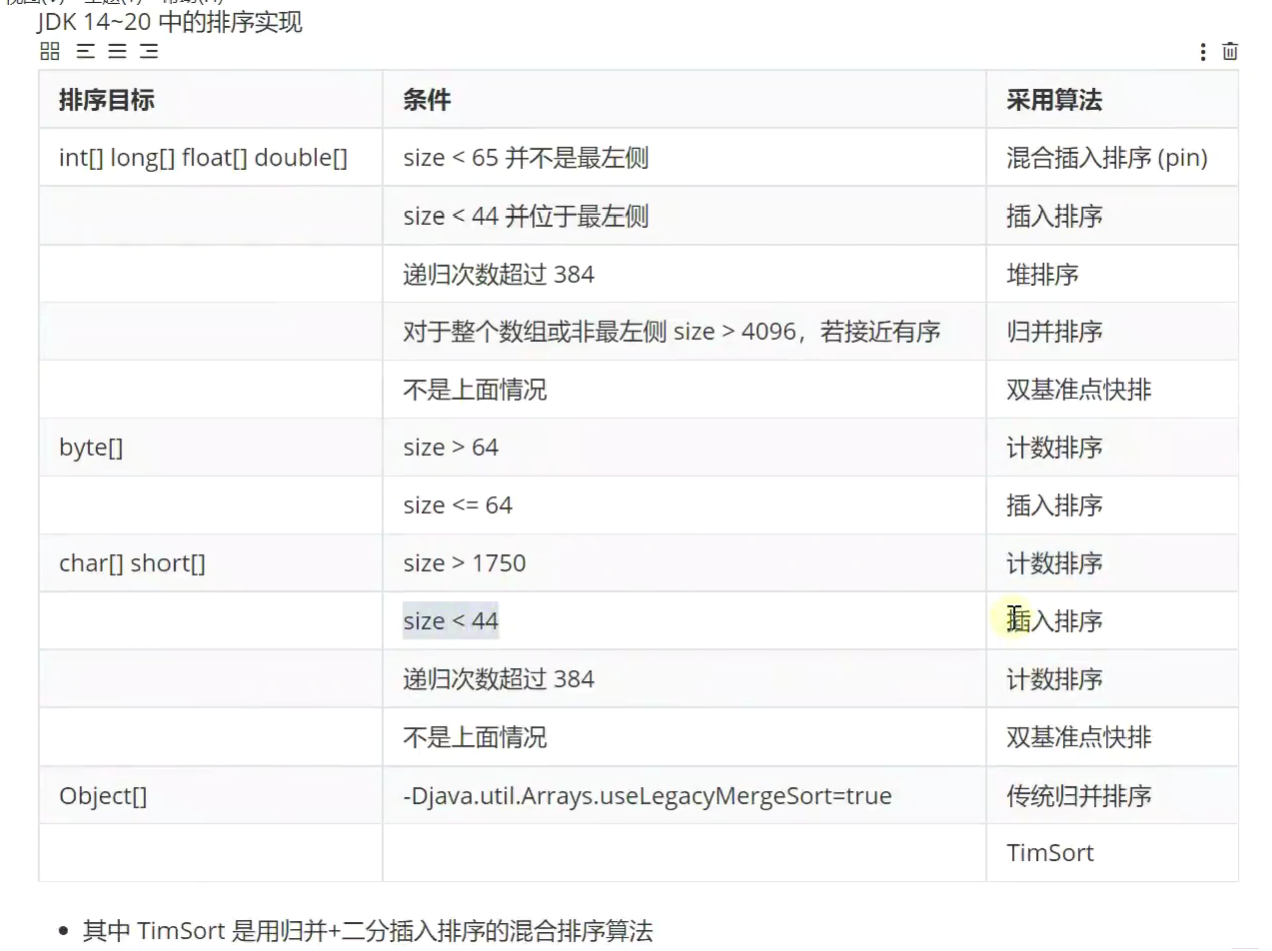
11.Java中的排序算法
7-13 JDK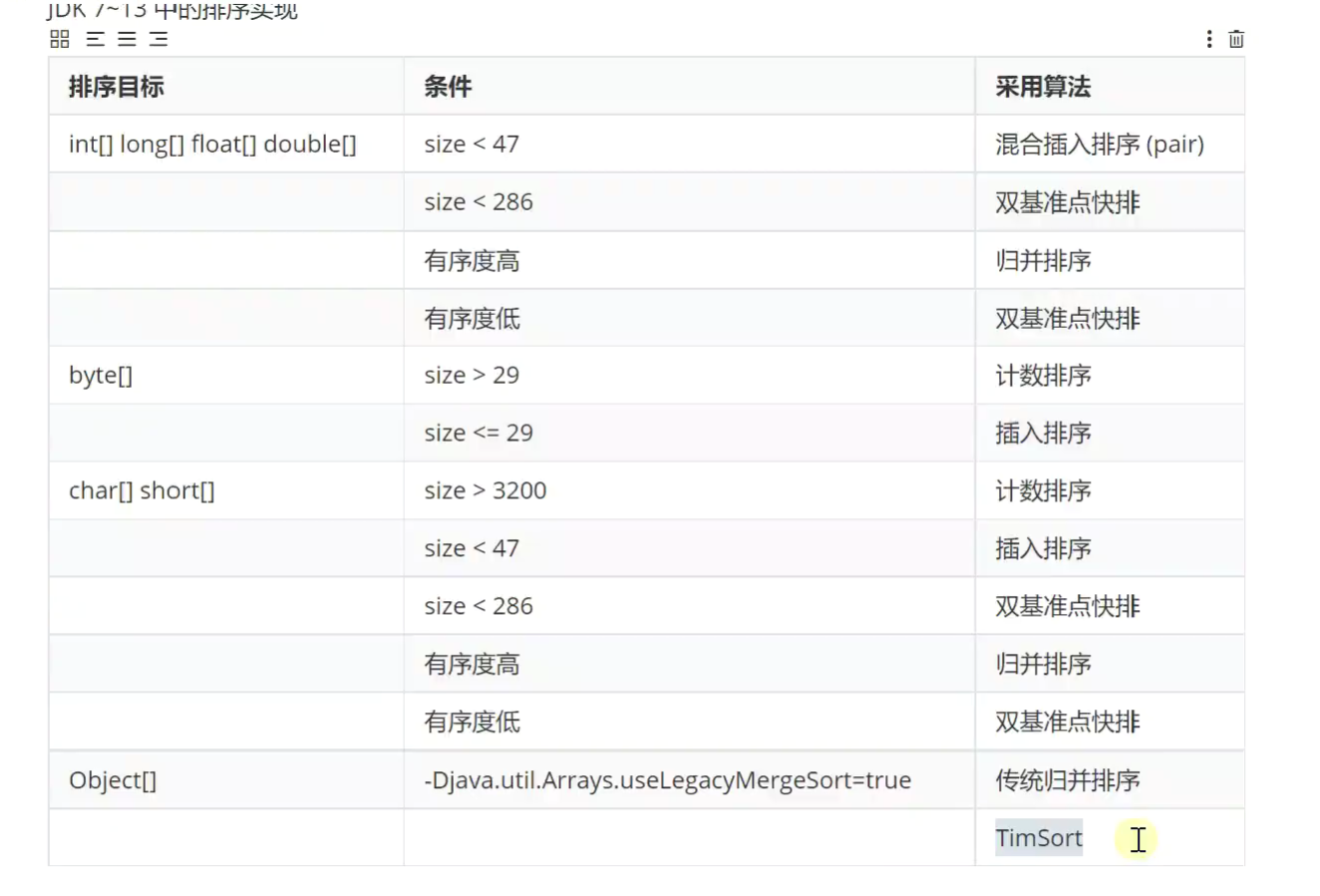
14-20JDK

-
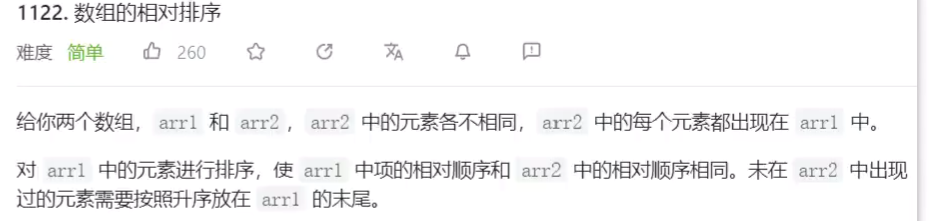
数组相对排序

-
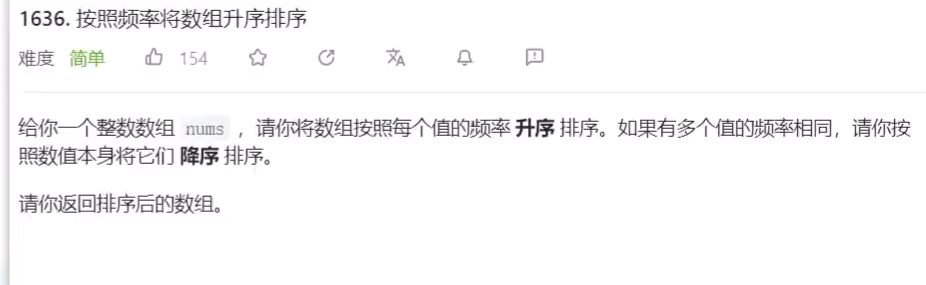
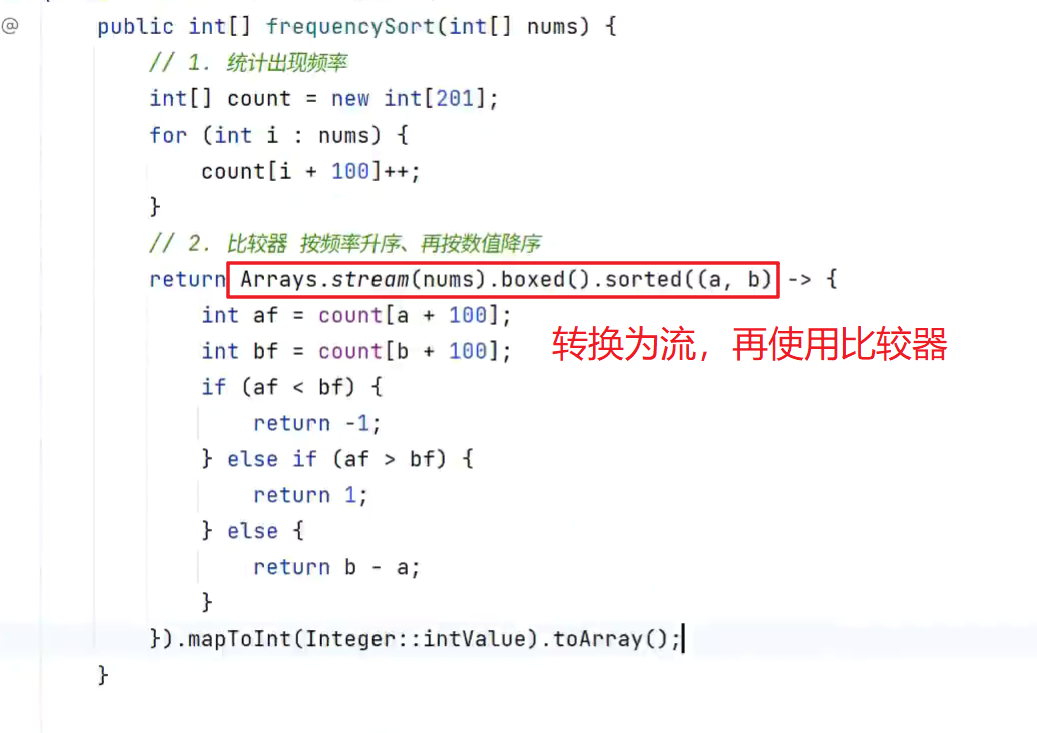
按照频率将数组升序排序

-
最大间距
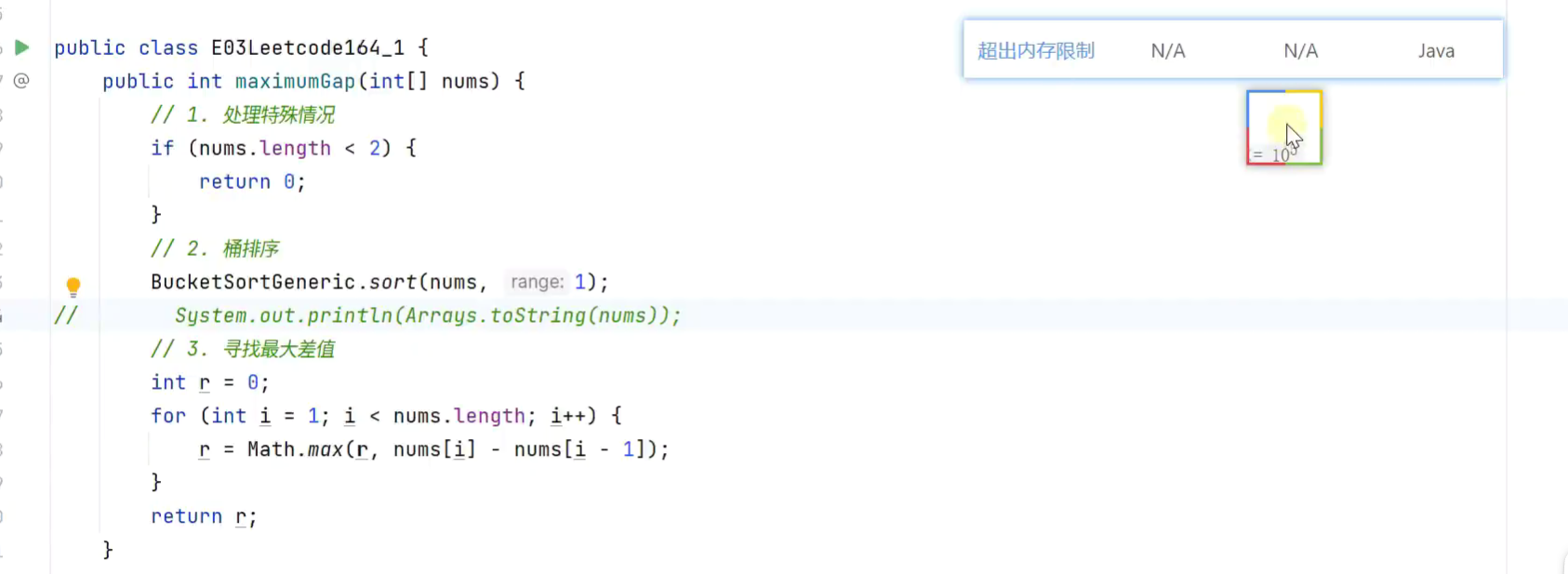
大范围数时,用桶排序的话,可能数组过大
基数排序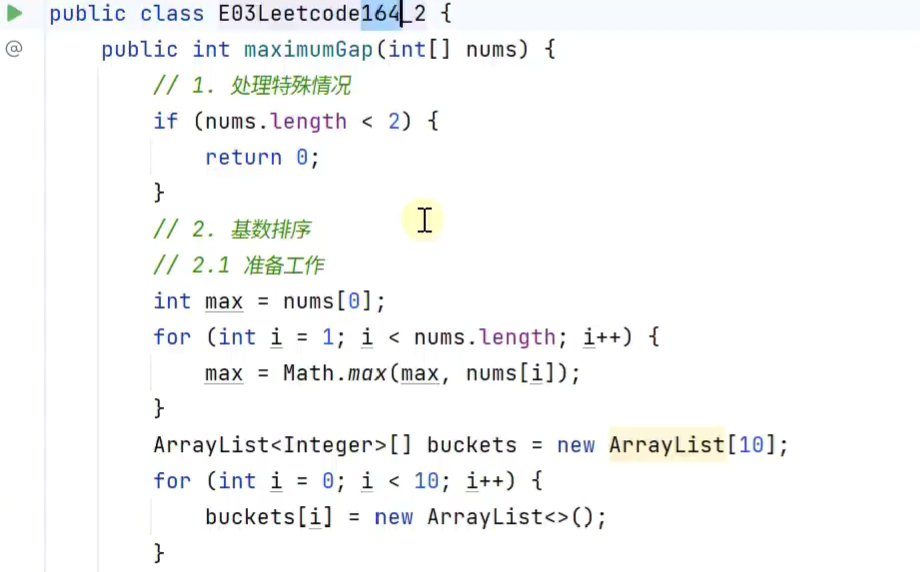

速度相比桶排序较低
改进桶排序
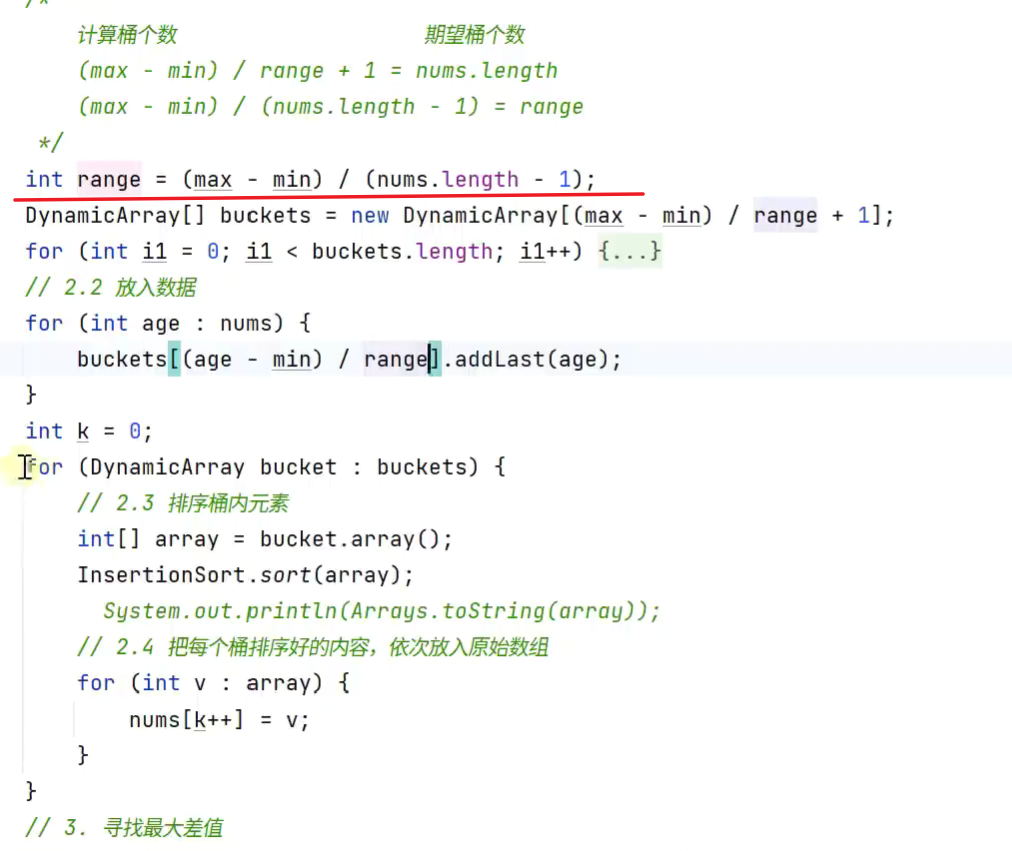
防止除0异常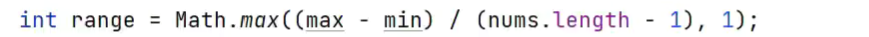
再优化
有空桶时,可以保证桶间间距大于桶内元素间距
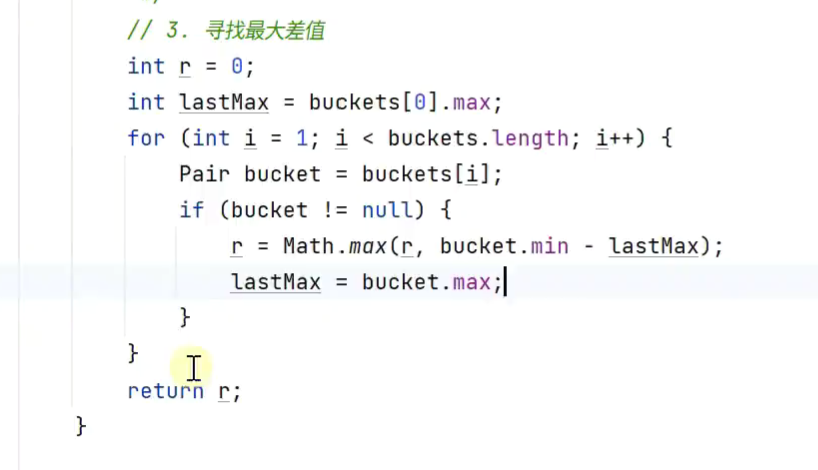
-
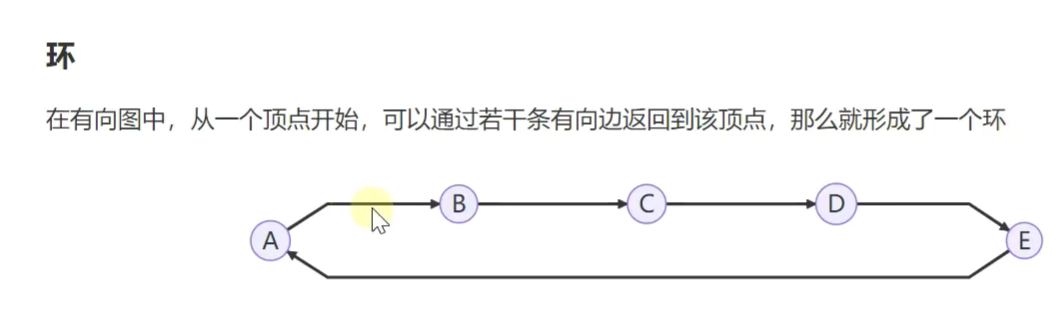
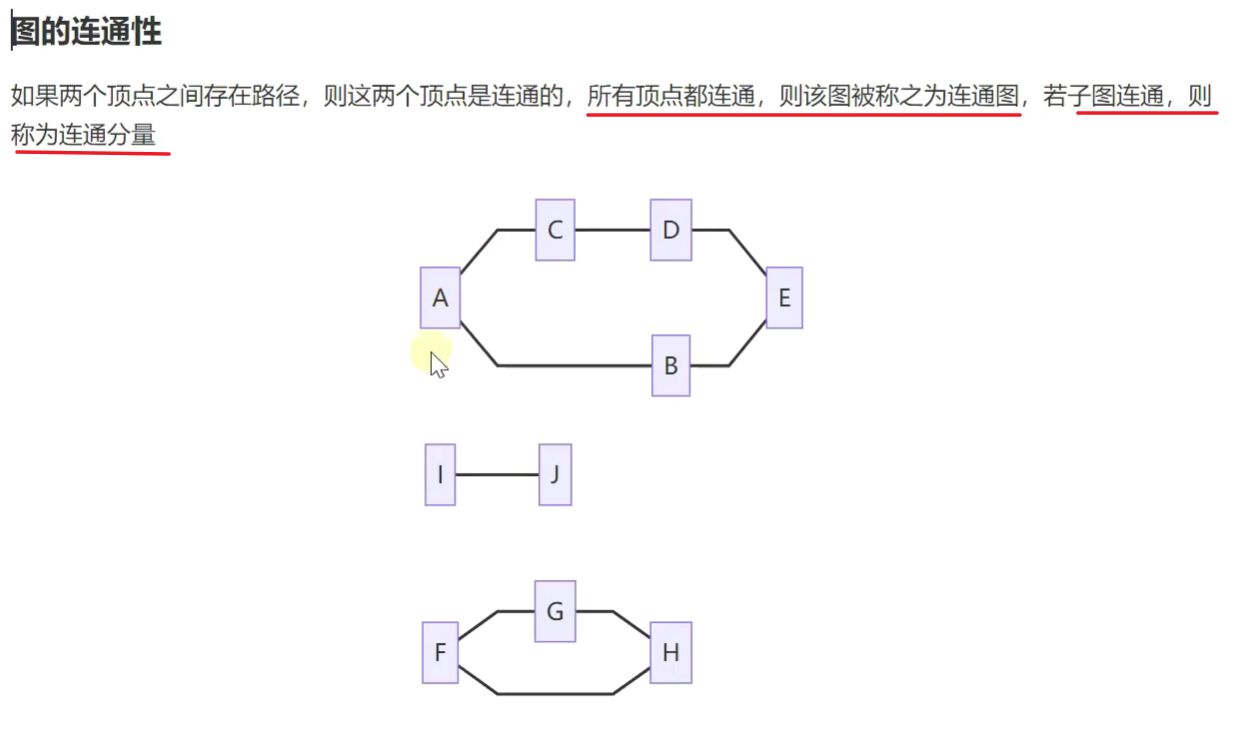
图
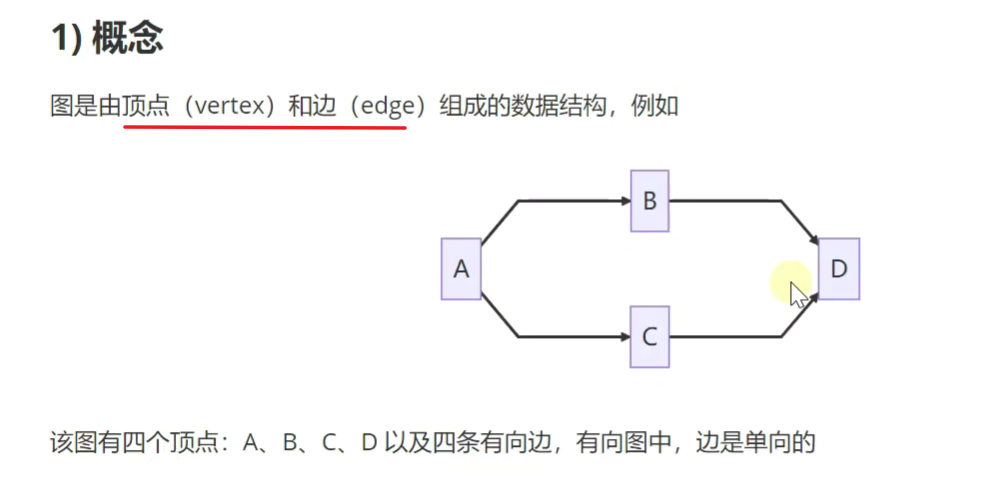
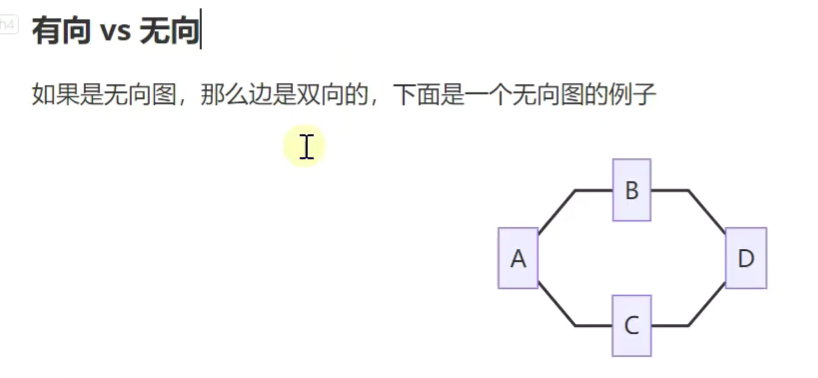
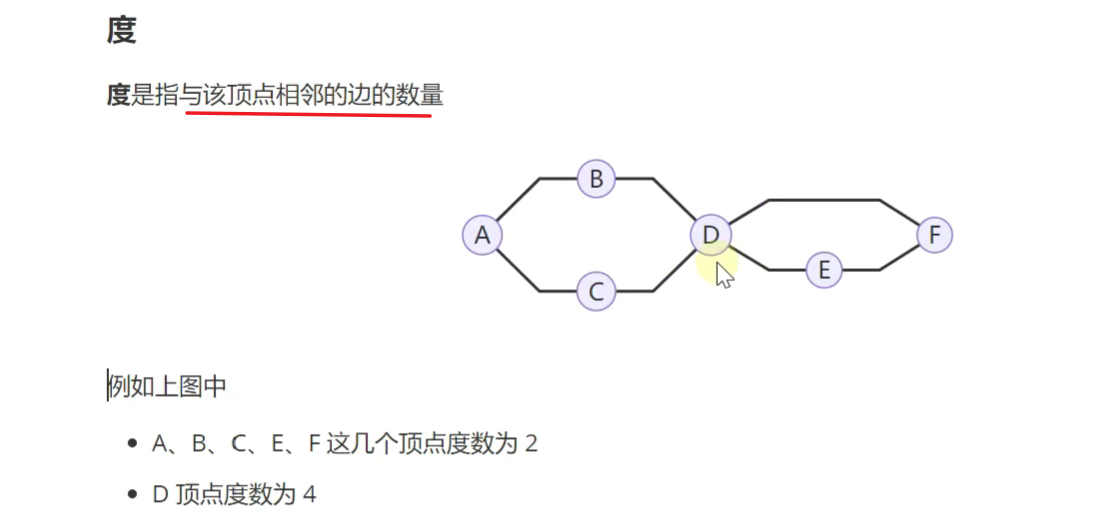 !
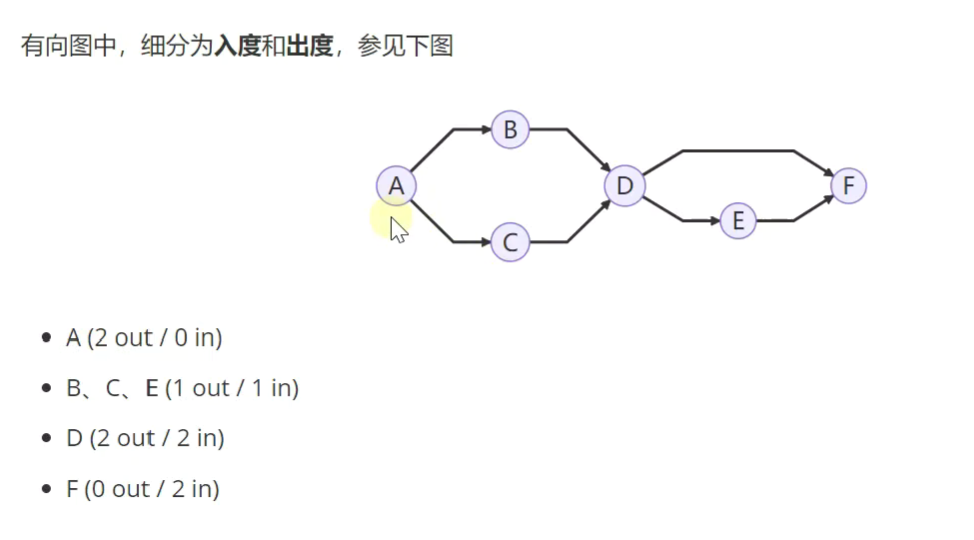
!
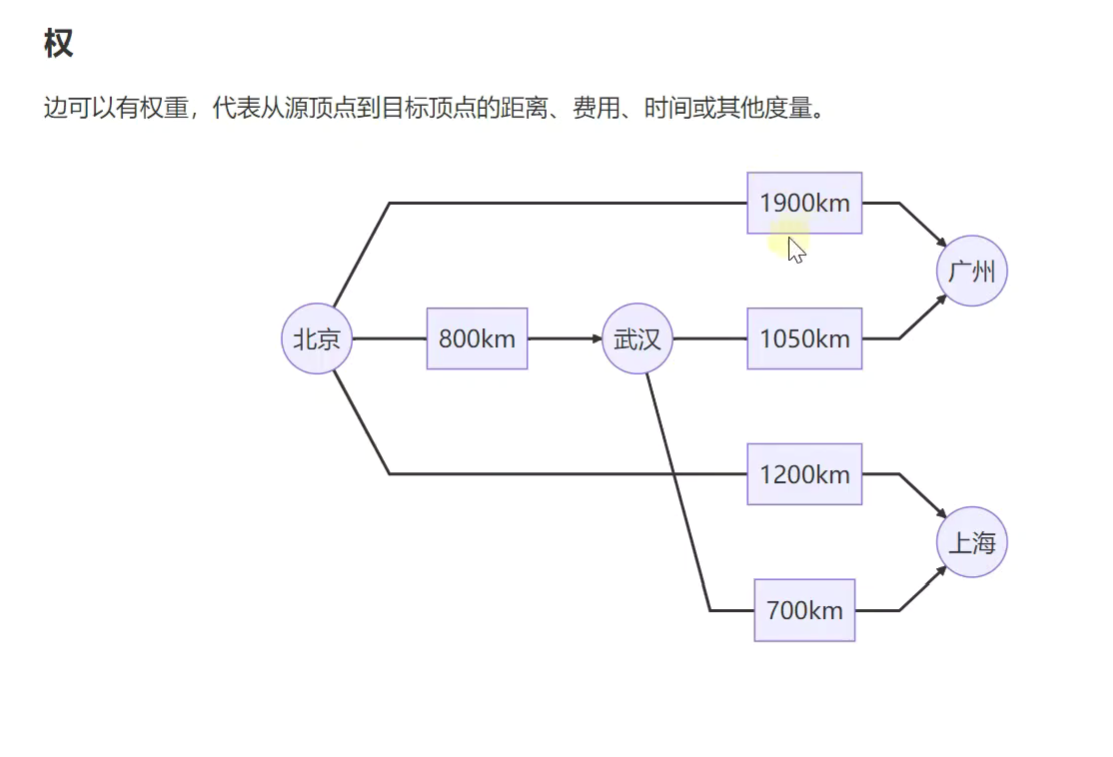

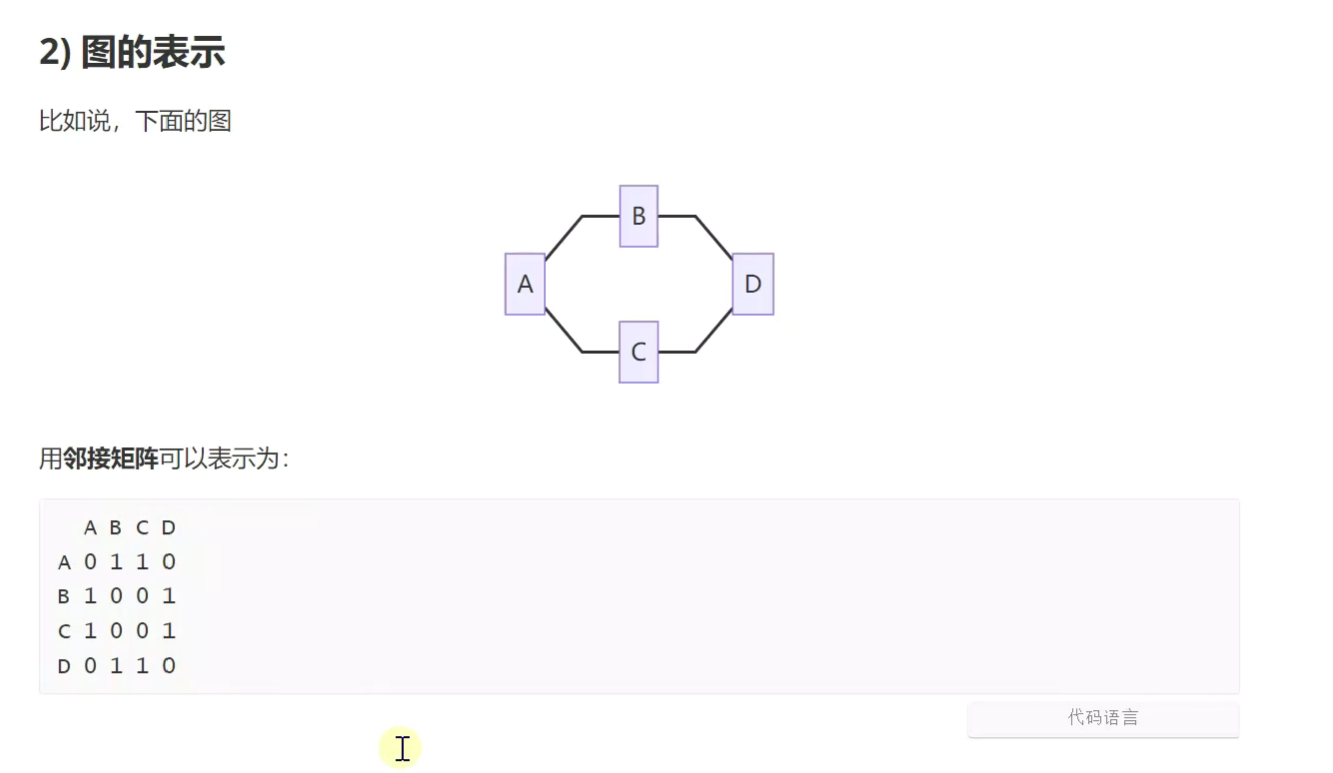
空间更节省

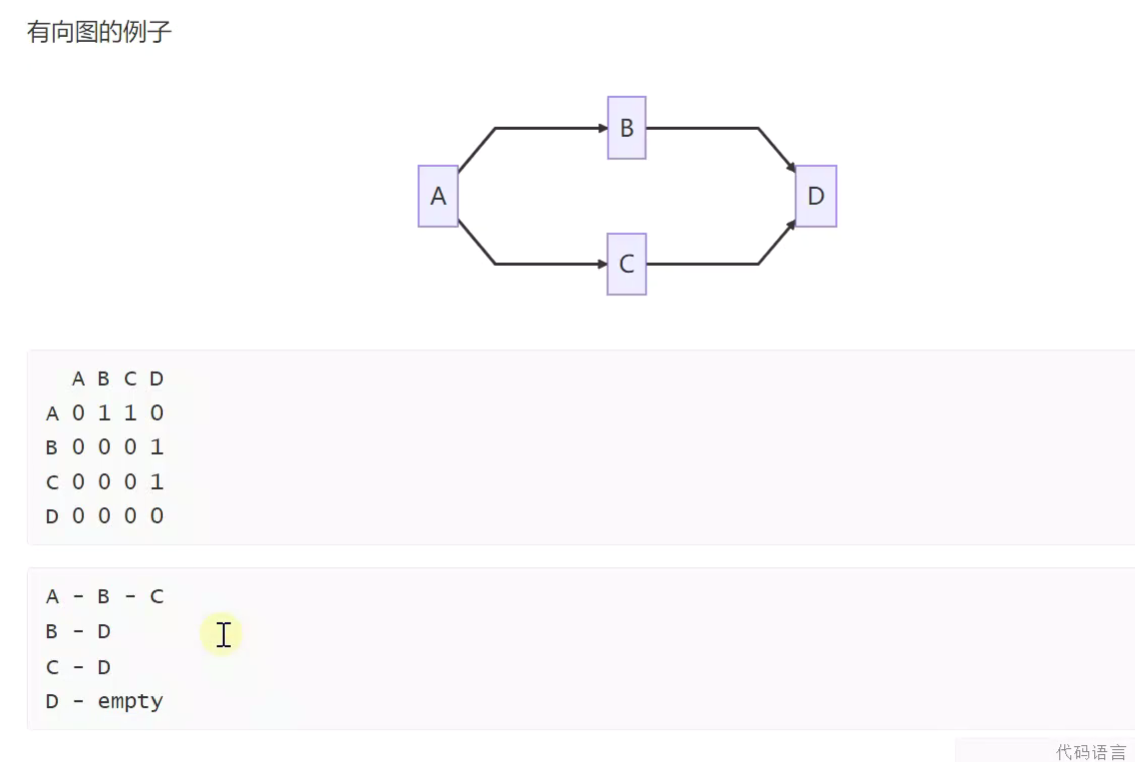
深度优先遍历
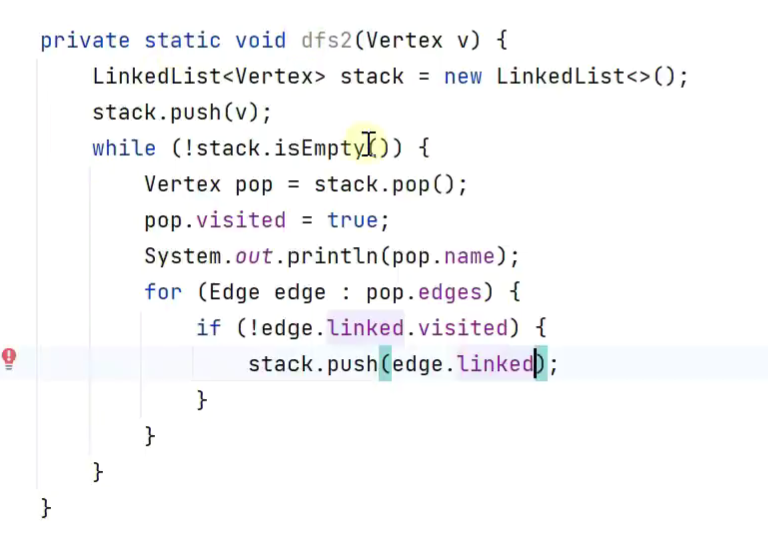
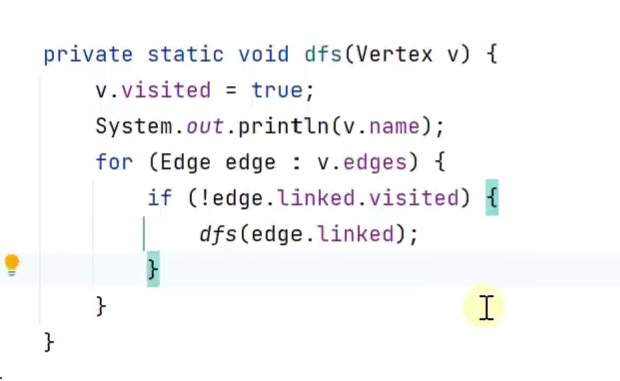
广度优先
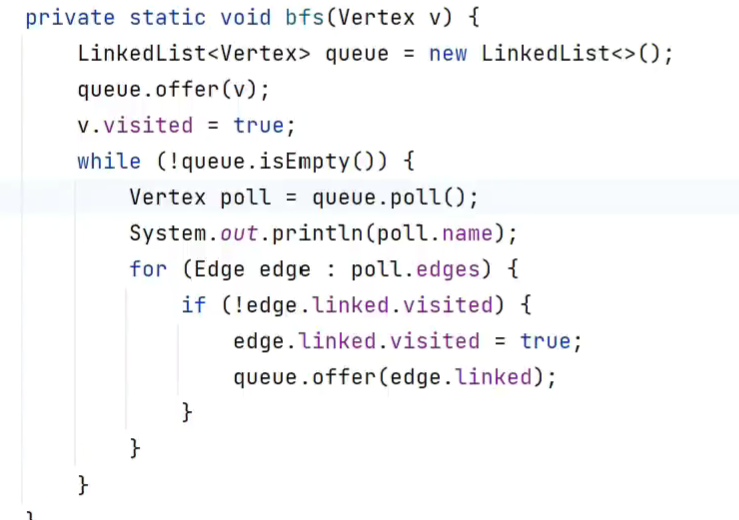
拓扑排序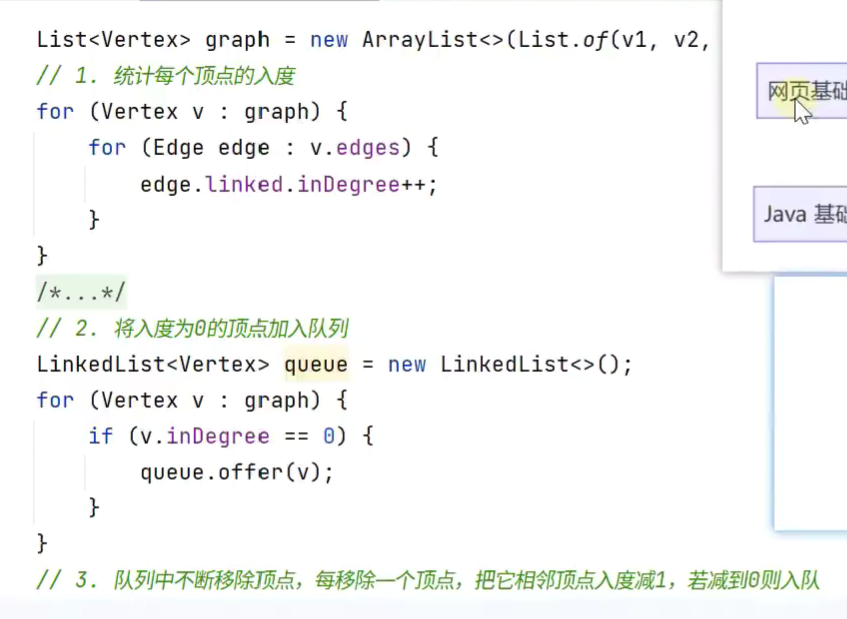
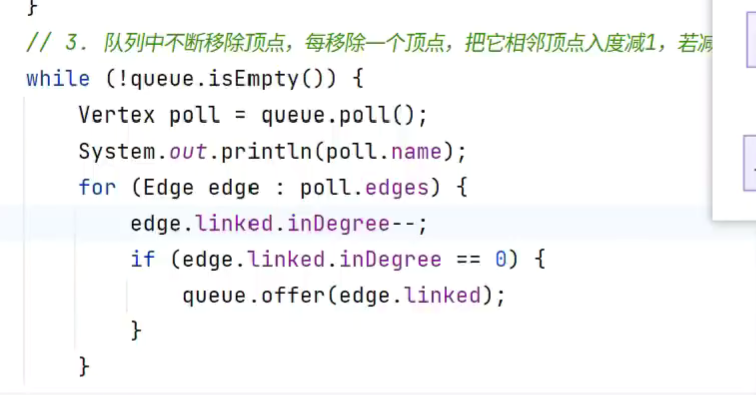
检测环

拓扑排序+深度优先

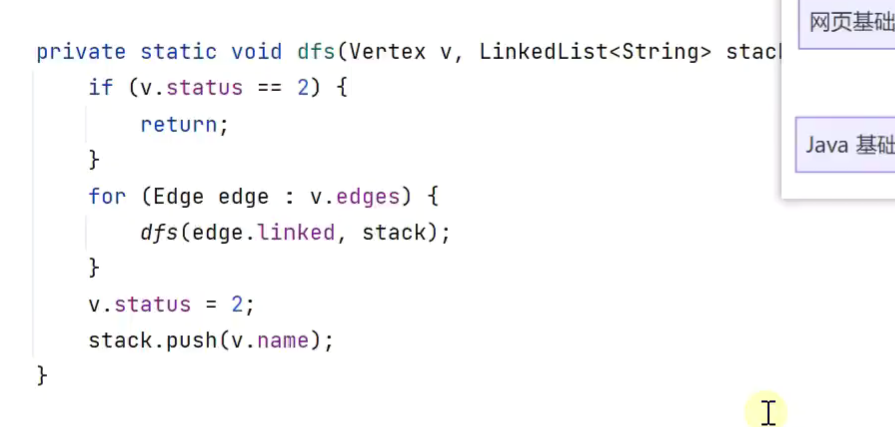
状态1用在 环检测
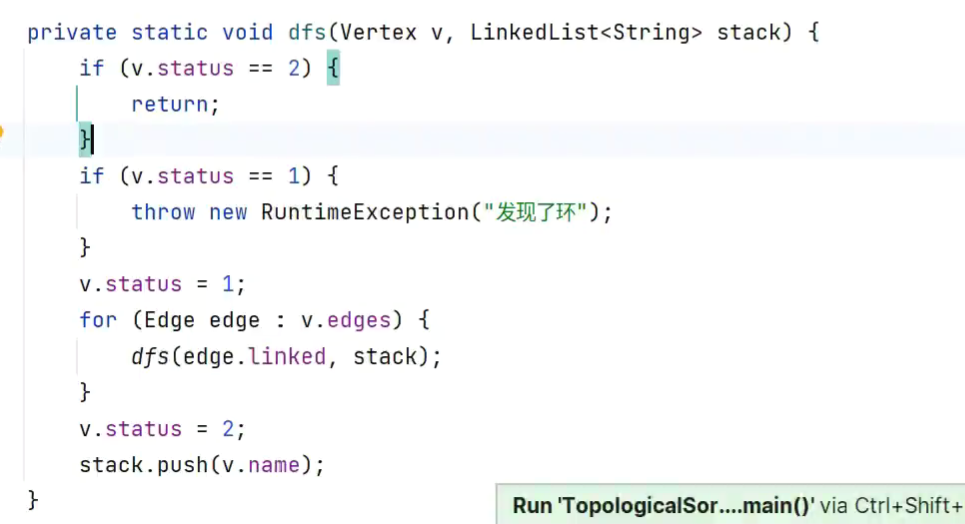
-
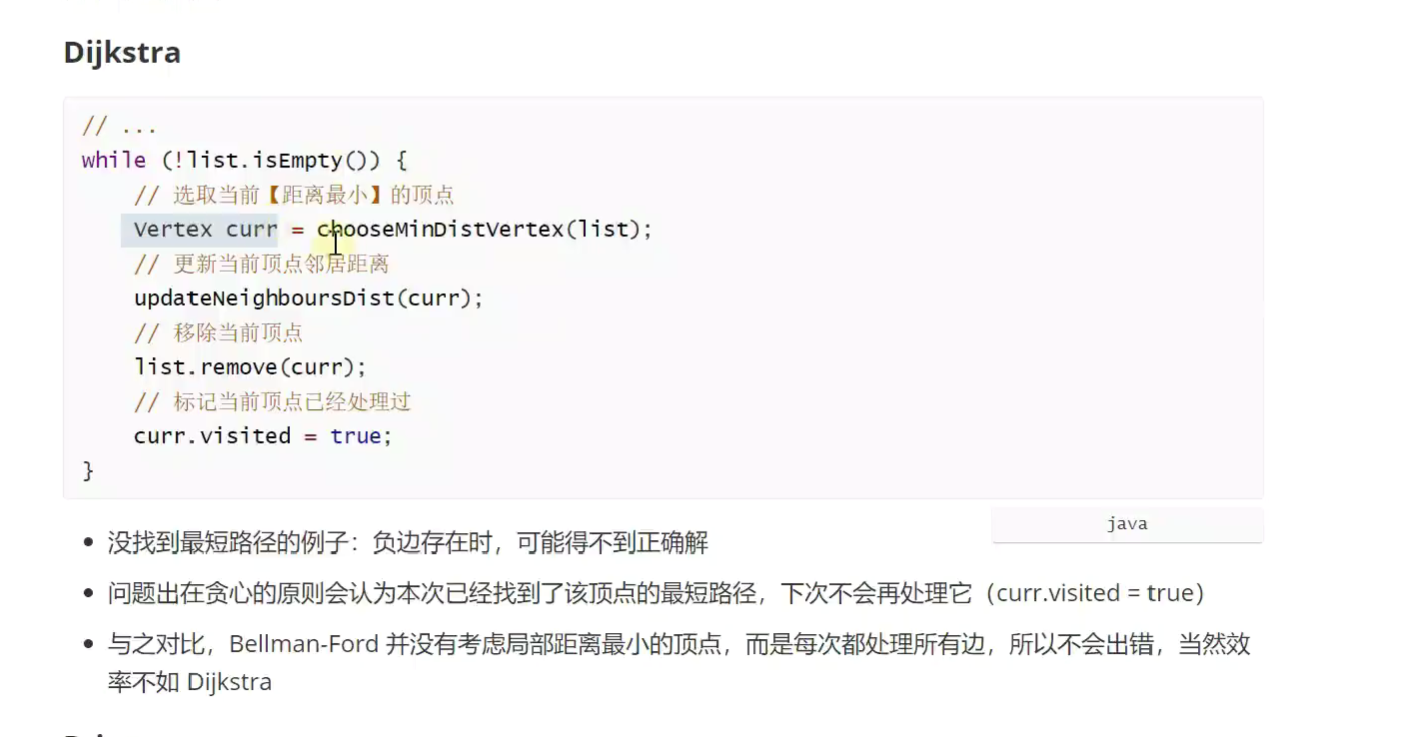
迪克斯特拉 单源最短路径算法

改进
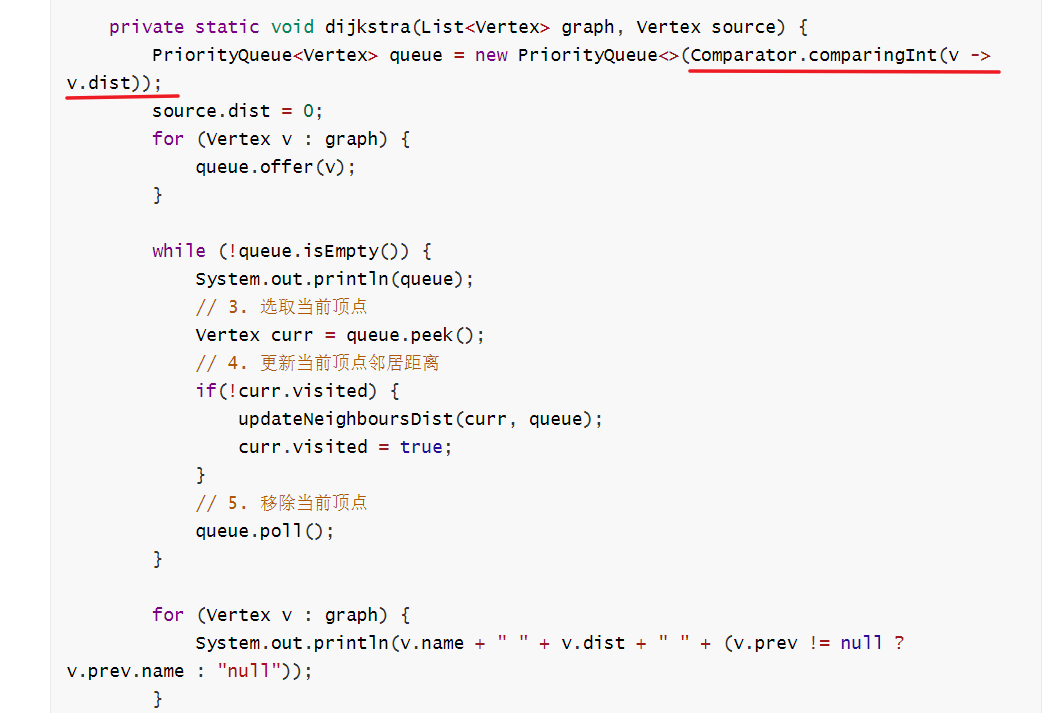
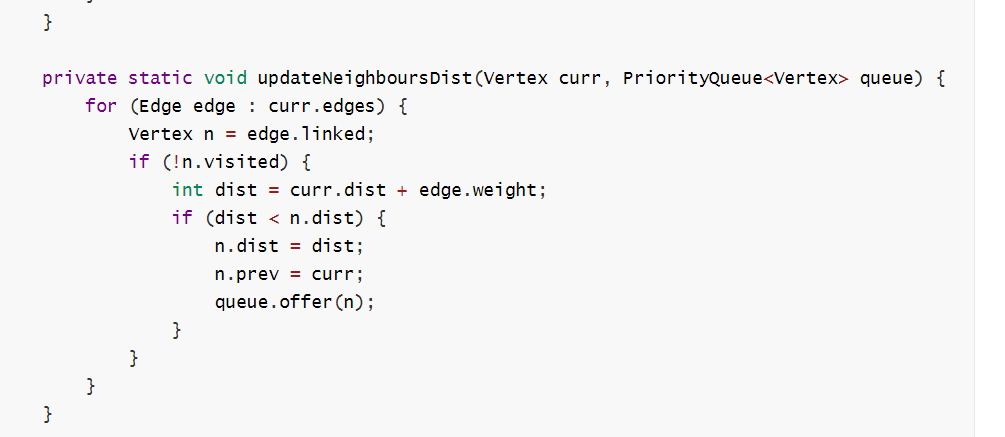
缺点:不能处理负权重 -
贝尔曼算法
可以处理负边 ,但不能处理负环,需手动检测
-
弗洛伊德多源最短路径算法

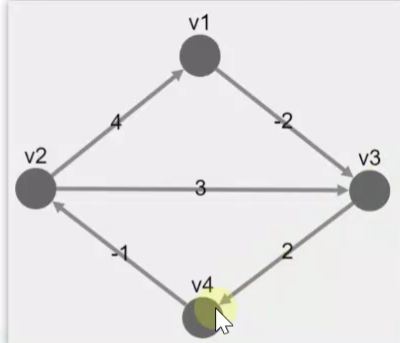
.....
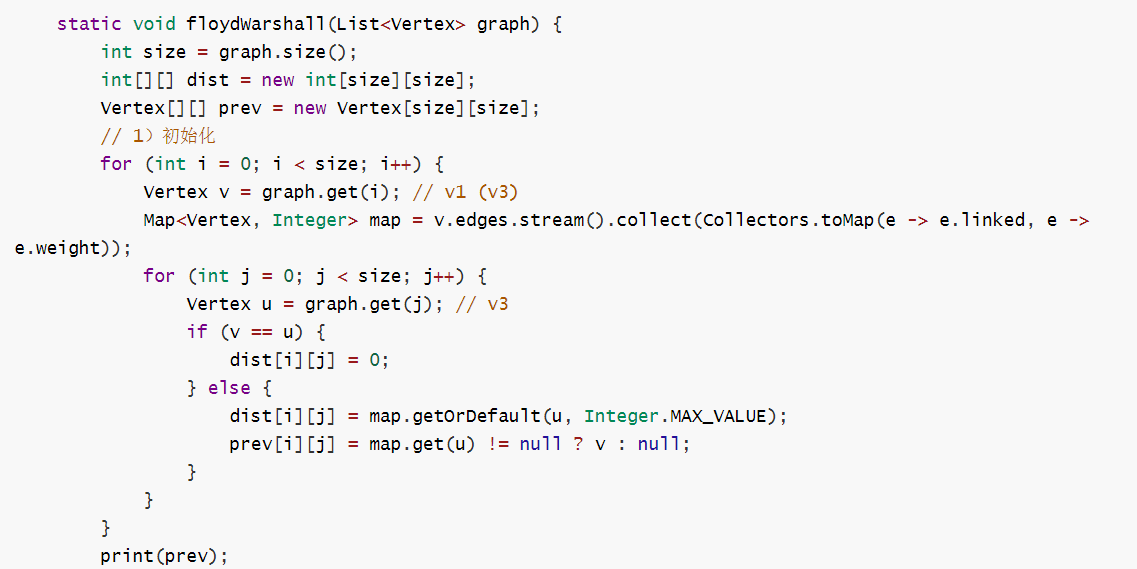


-
最小生成树
Prim算法(以顶点为核心)
和迪克斯特拉算法很相似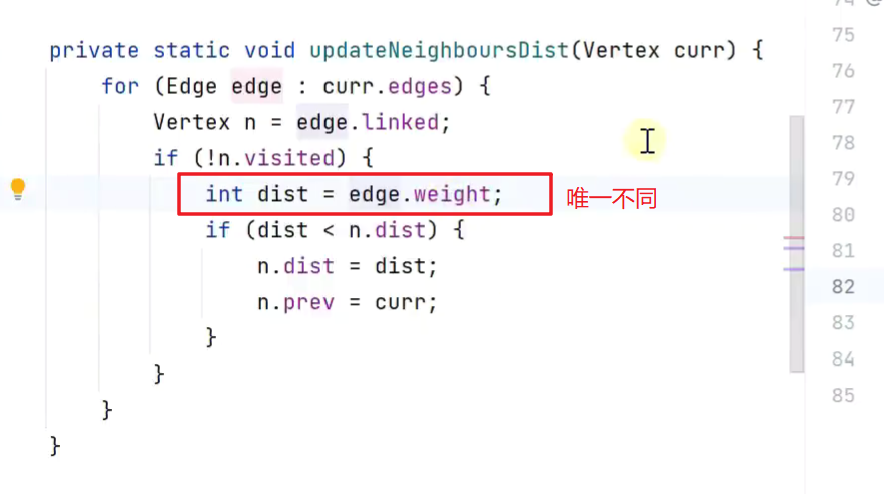
克鲁斯卡尔算法(以边为核心)
从小到大找边,看边的两点是否未被联通
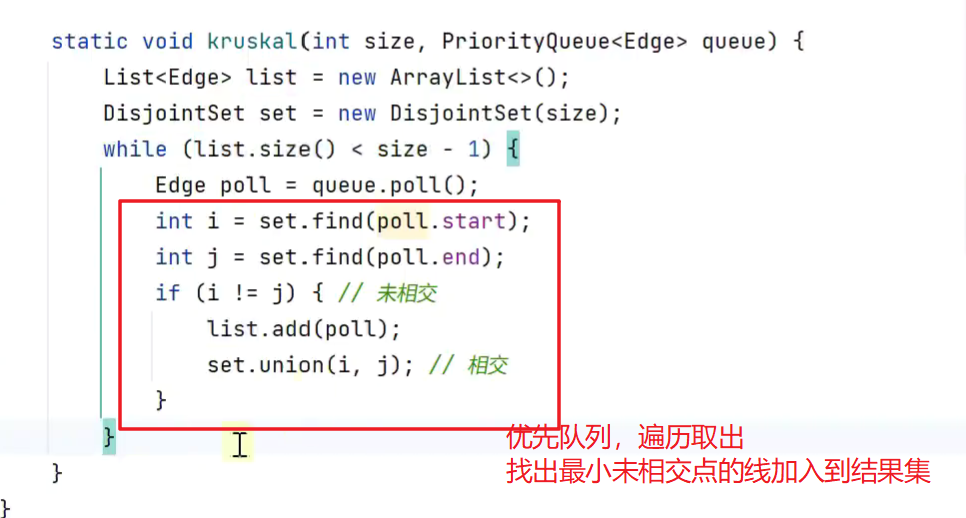
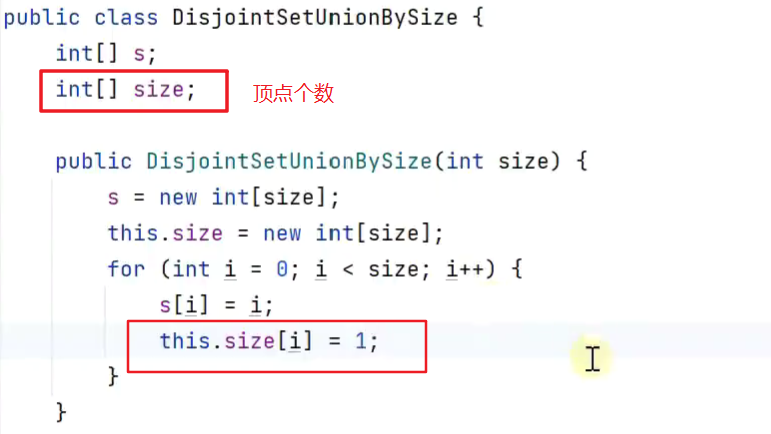
不相交集合类
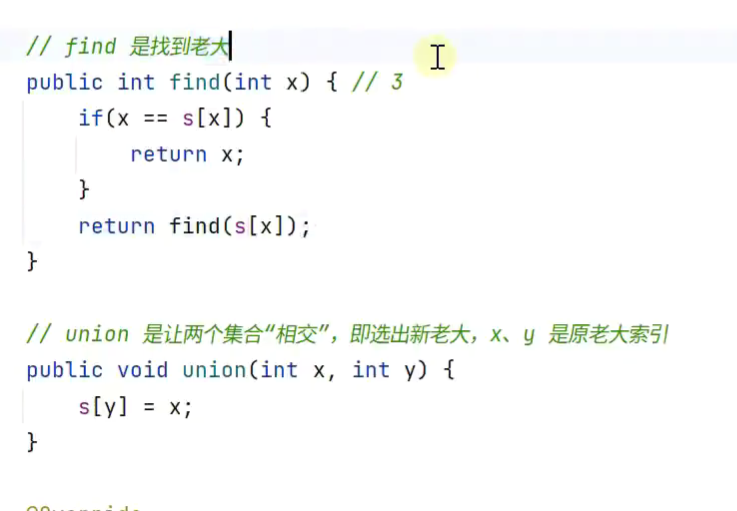
最坏情况
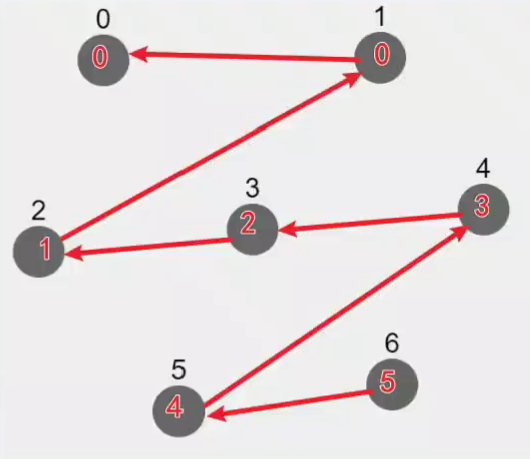
优化find优化,路径压缩

优化union
找到更合适的老大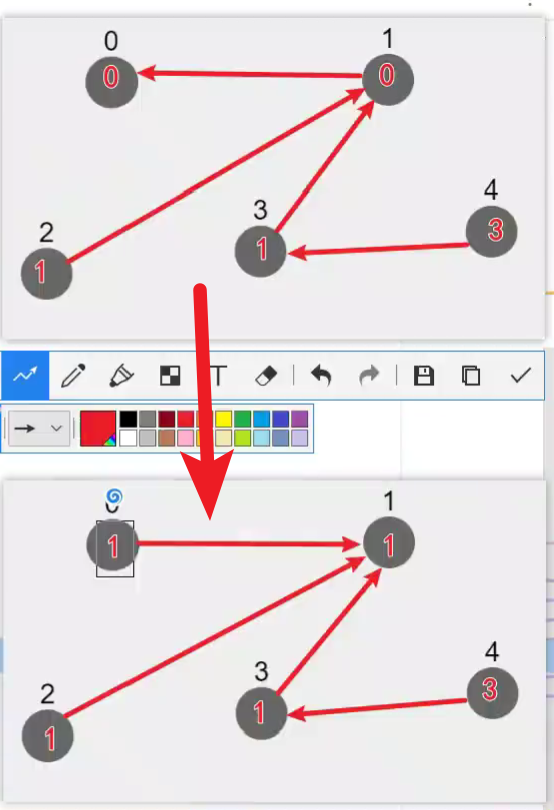

-
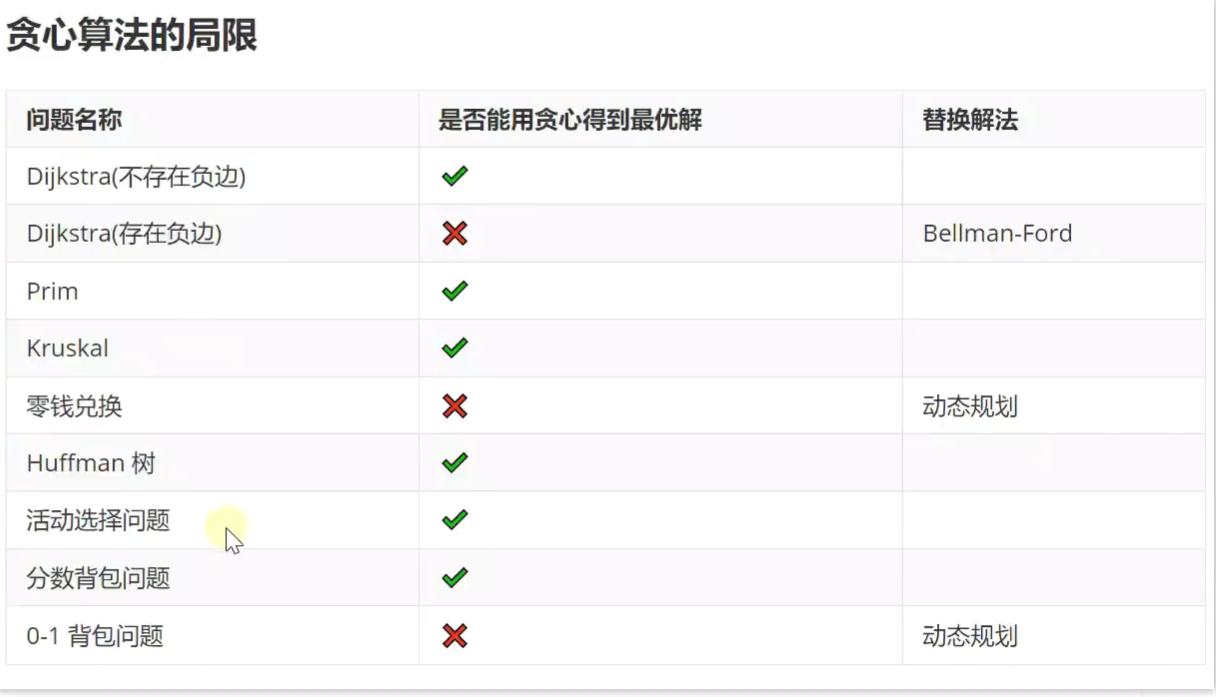
贪心算法
寻找最优解

-
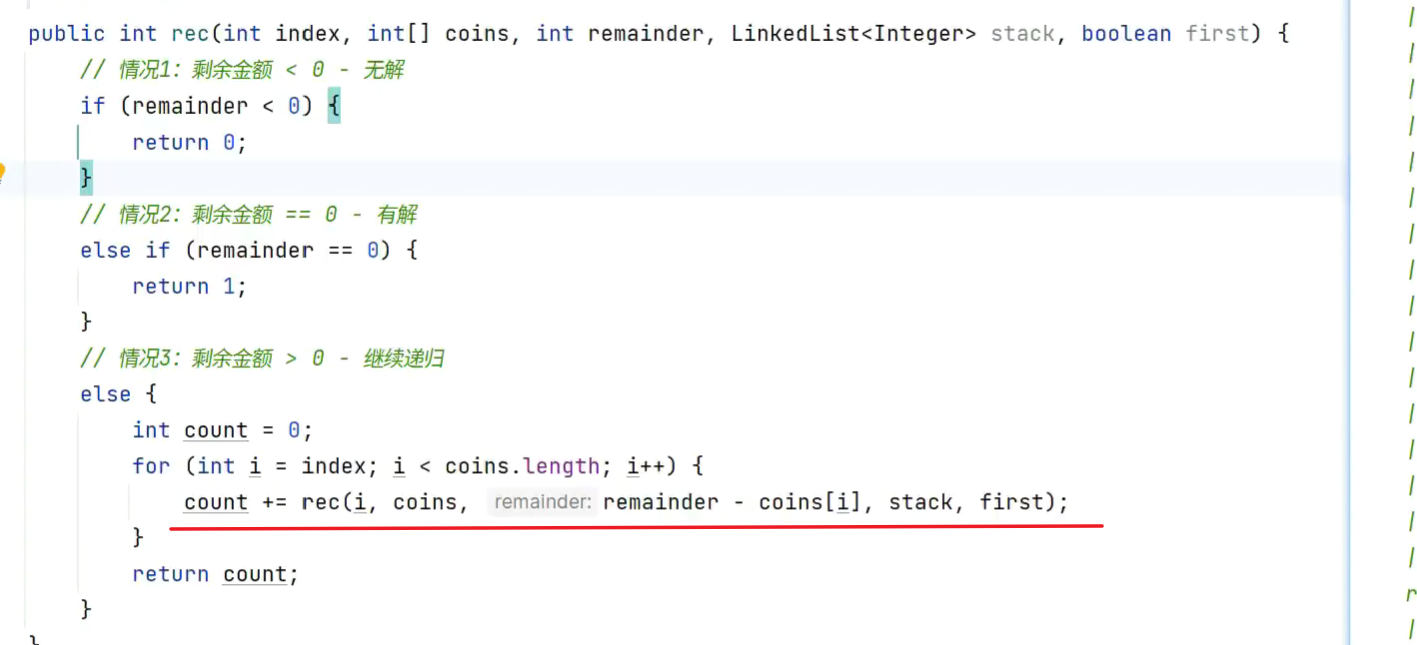
零钱兑换

递归


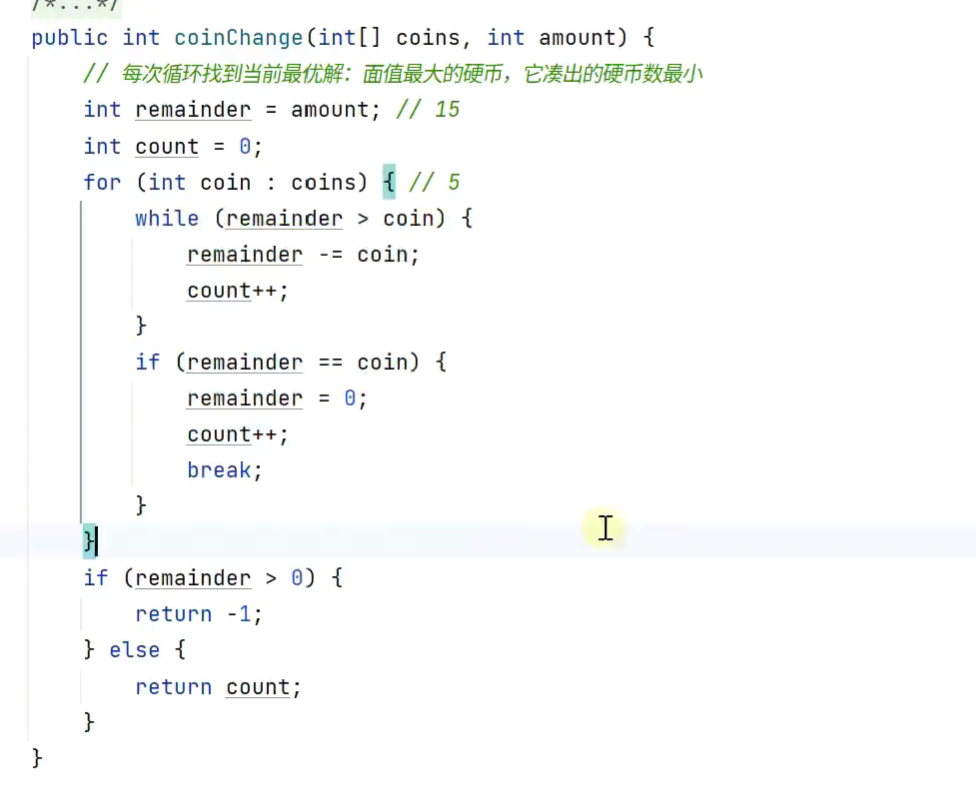
利用贪心算法
可能得到错误结果
-
霍夫曼编码
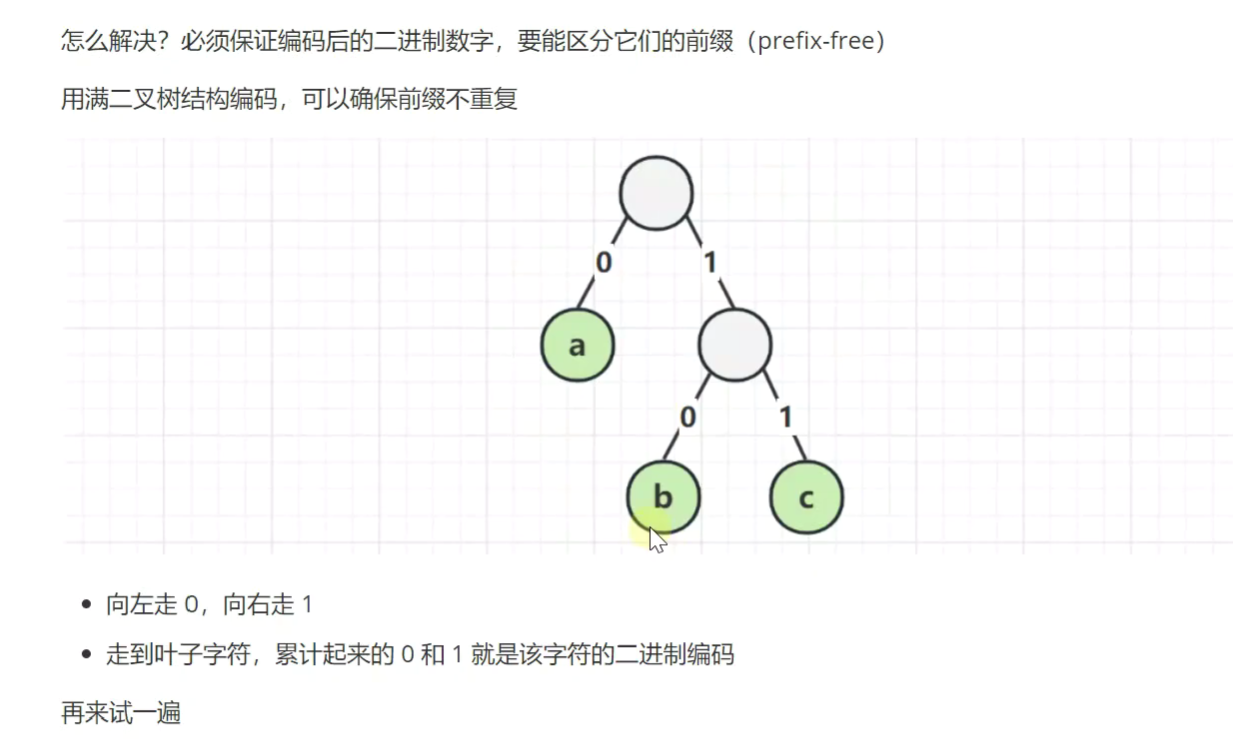
 0
0 
统计各个字符的出现频次

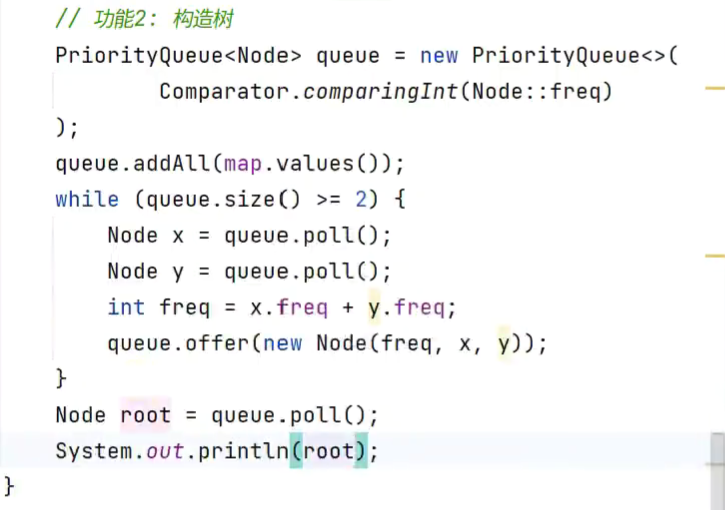
构造树
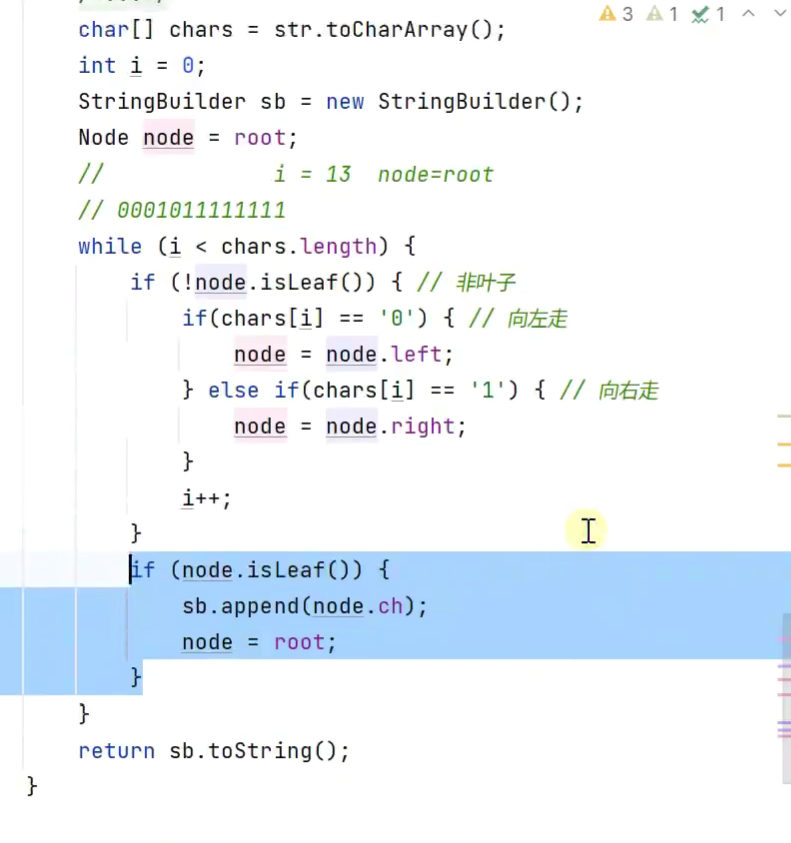
编码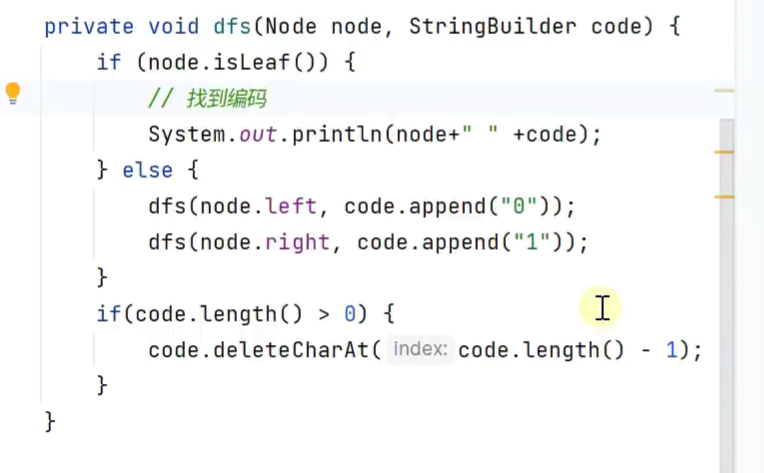
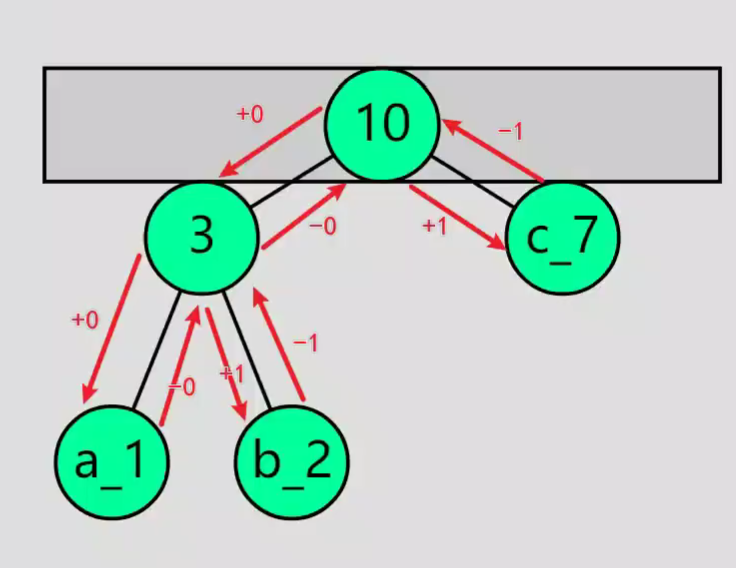

解码
-
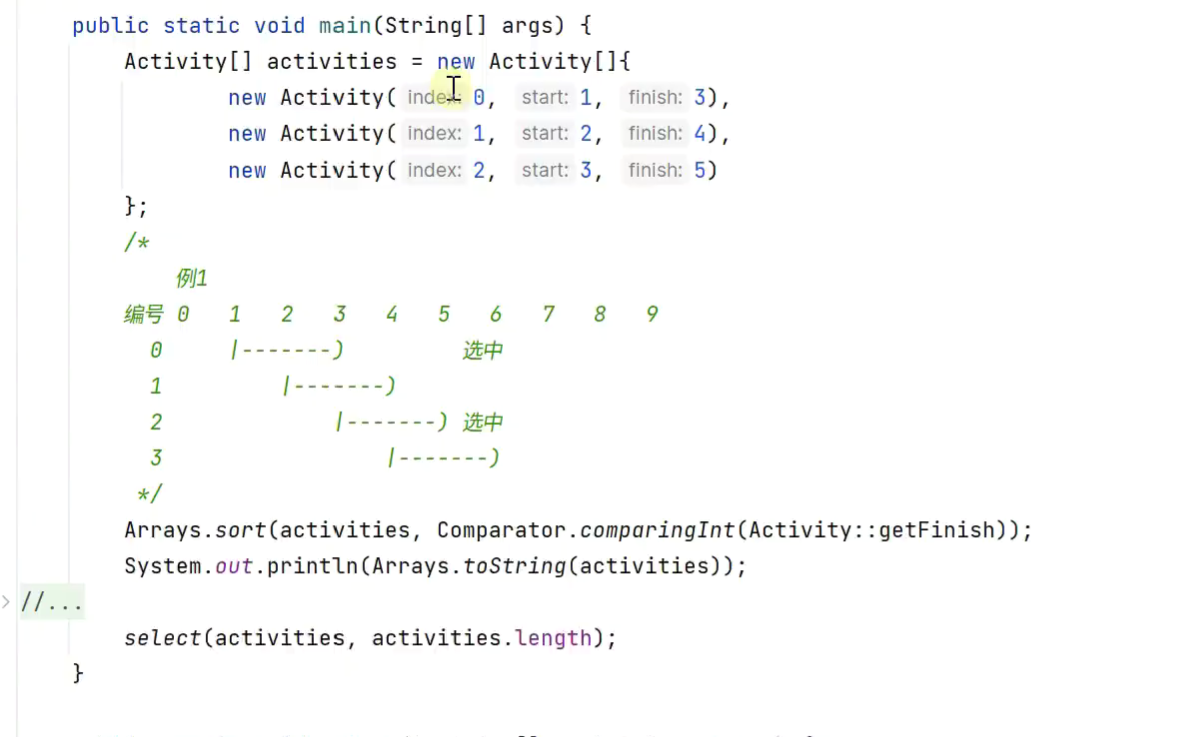
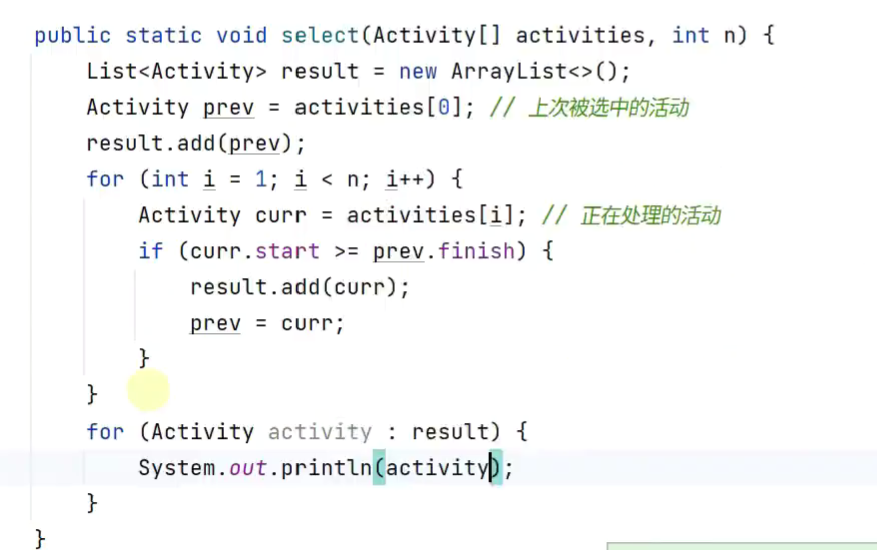
活动选择

贪心算法
优先选择最先结束的活动
’
-
分数背包问题


-
-
动态规划 解决斐波那契


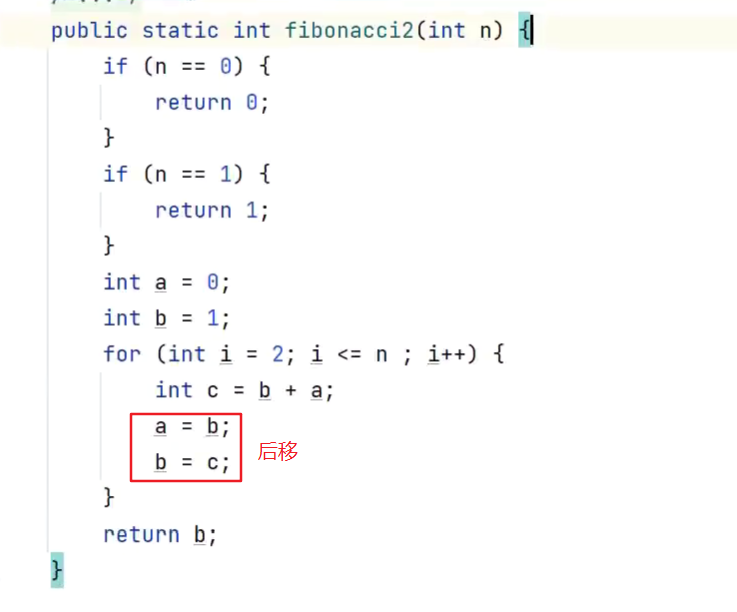
-
贝尔曼算法求最短路径
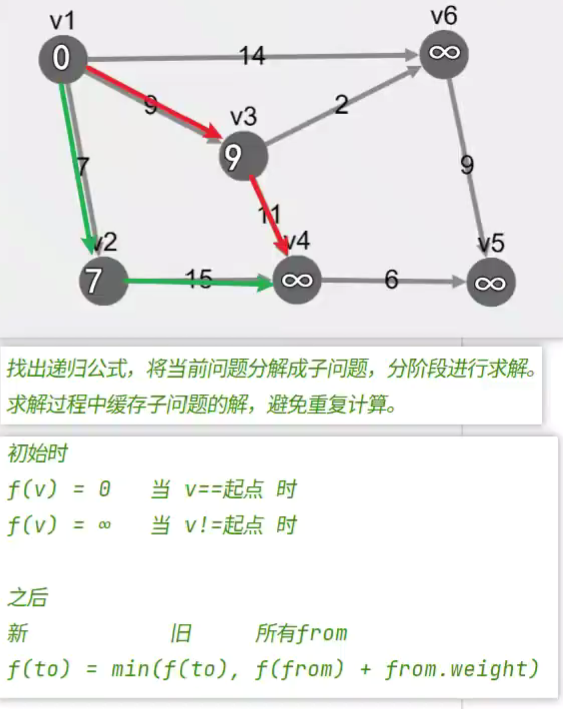

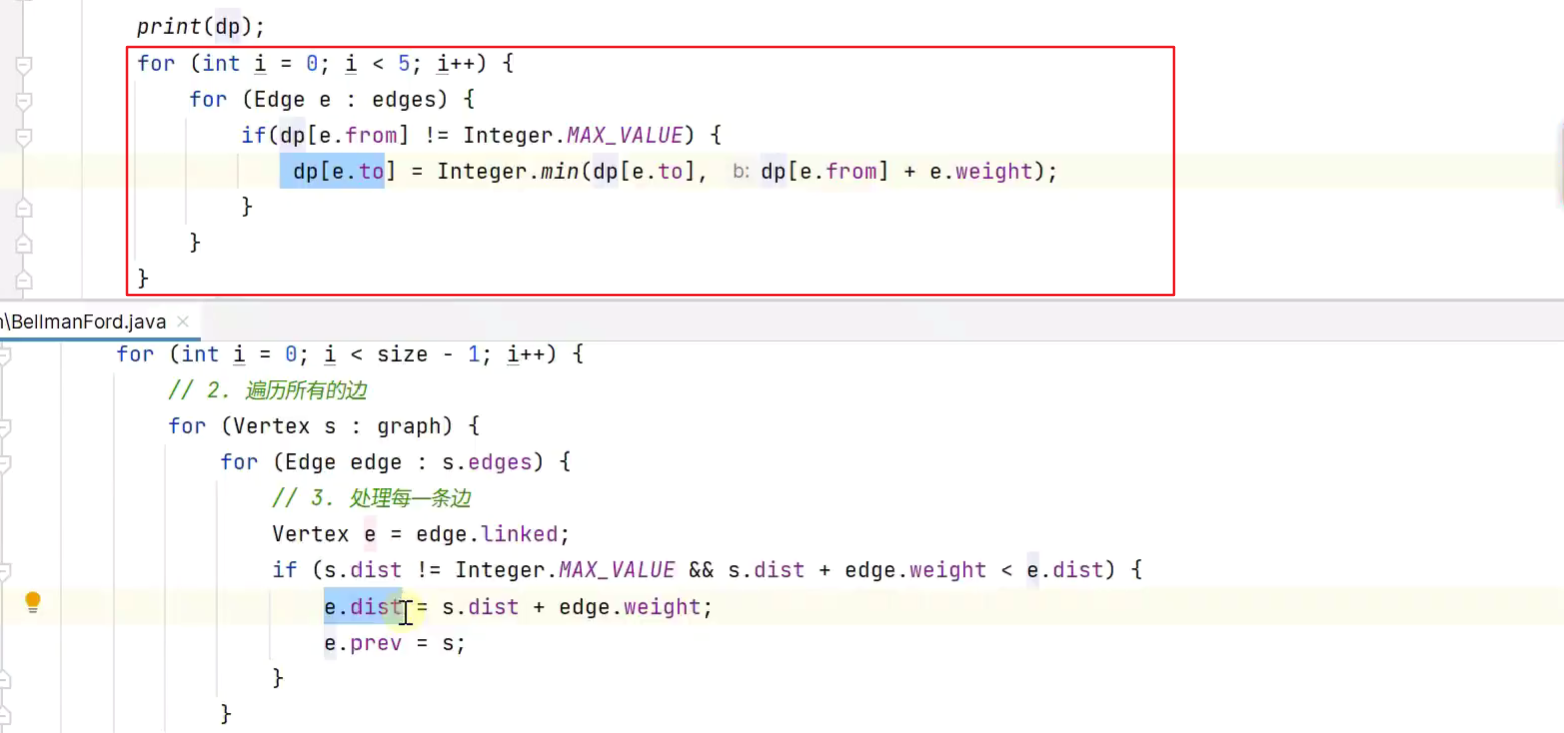
-
路径问题
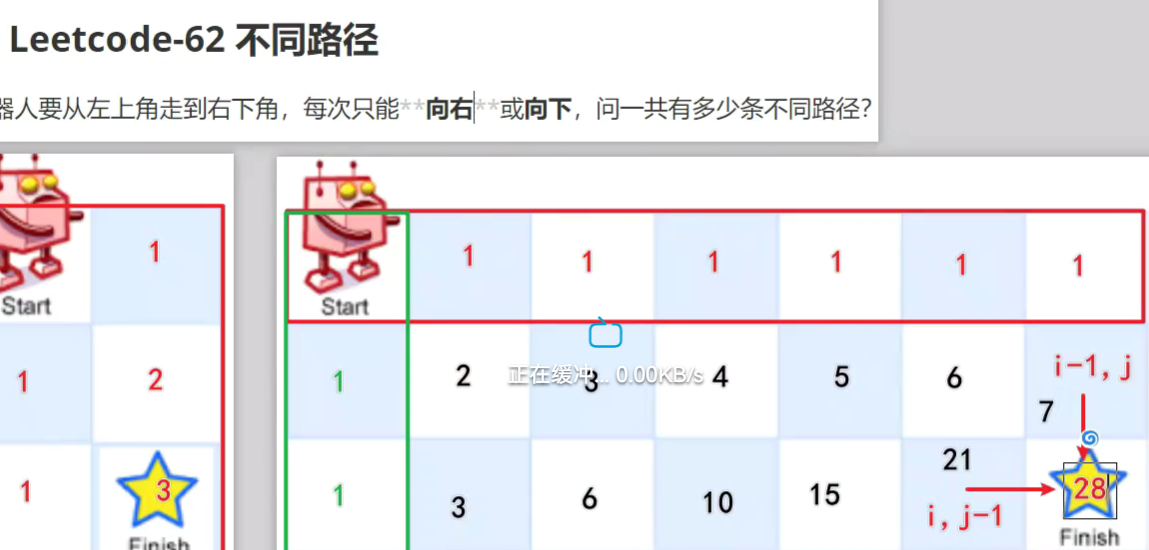
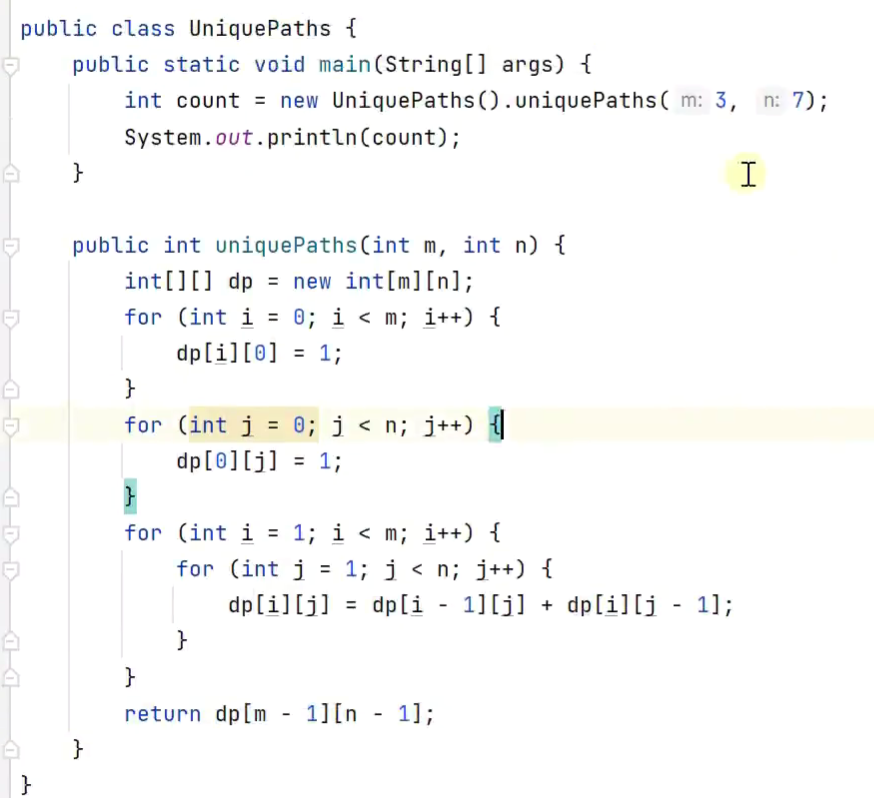
改为一维数组表示
原值为上次继承到的值,与左值相加即为新值
-
背包问题
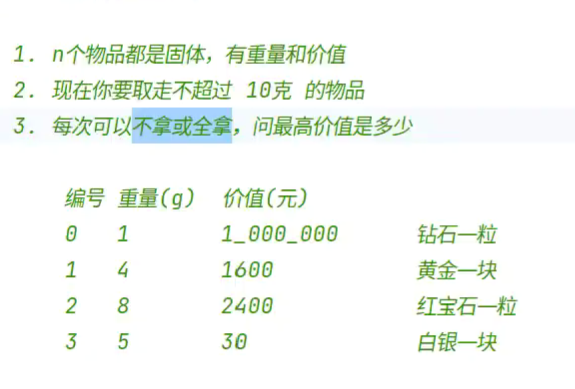
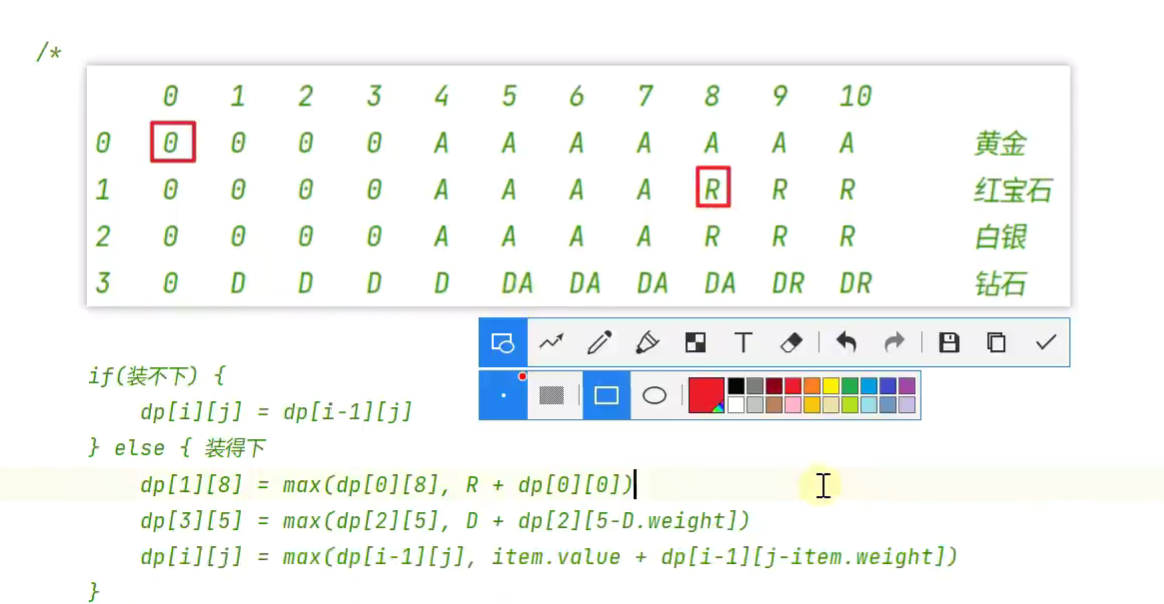

优化,二维数组降为一维数组
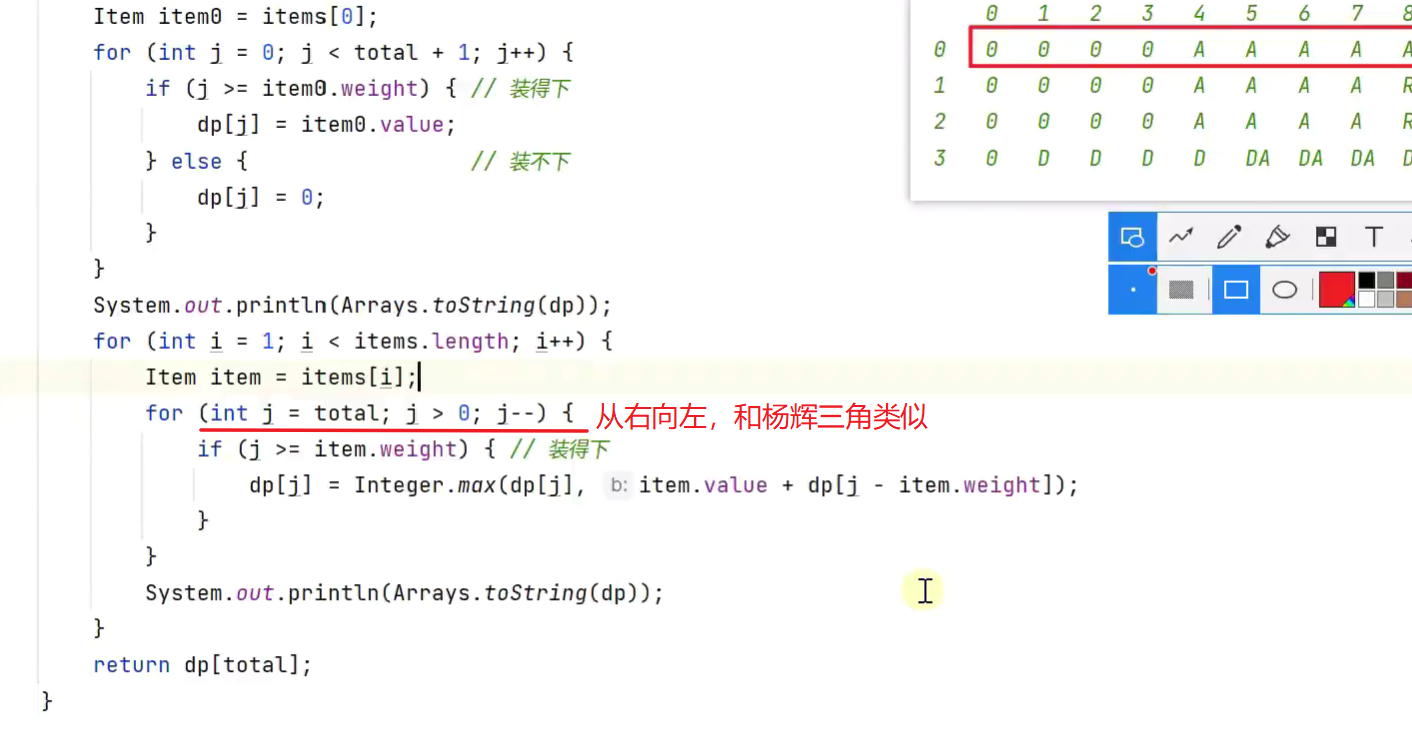
-
完全背包问题
每件物品无限多
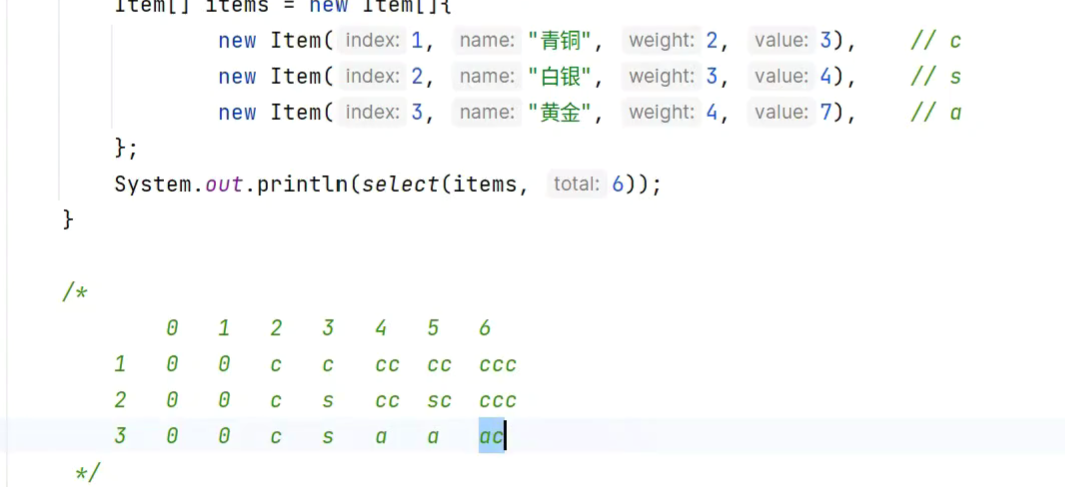
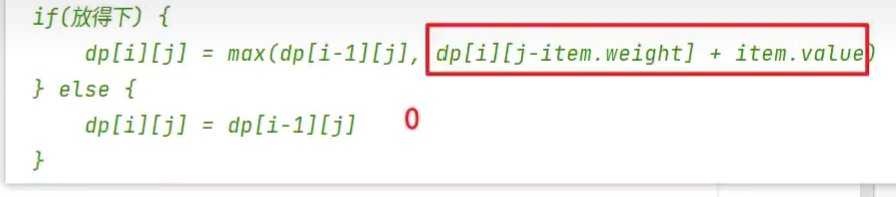
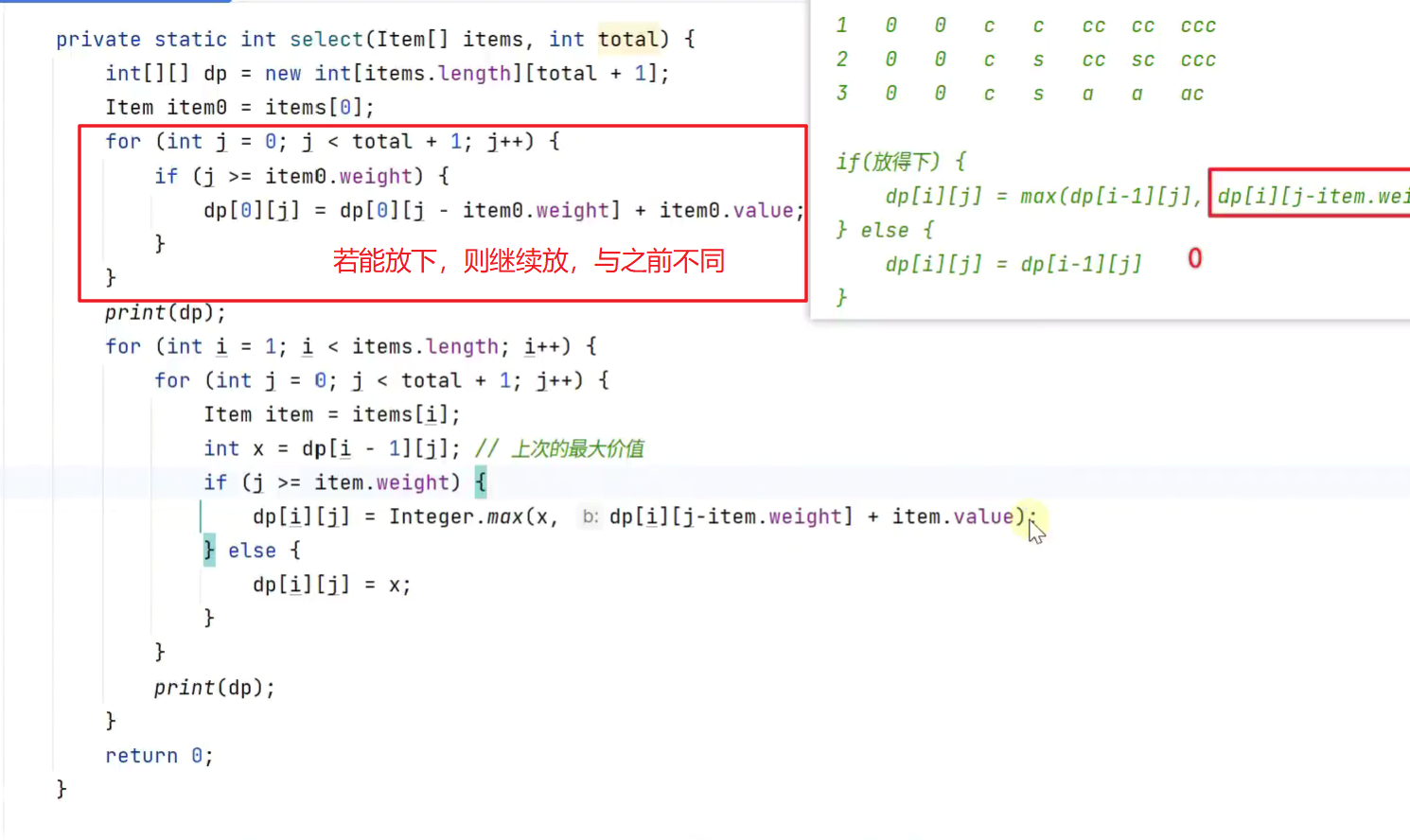

降维,为什么j的遍历顺序不用改变
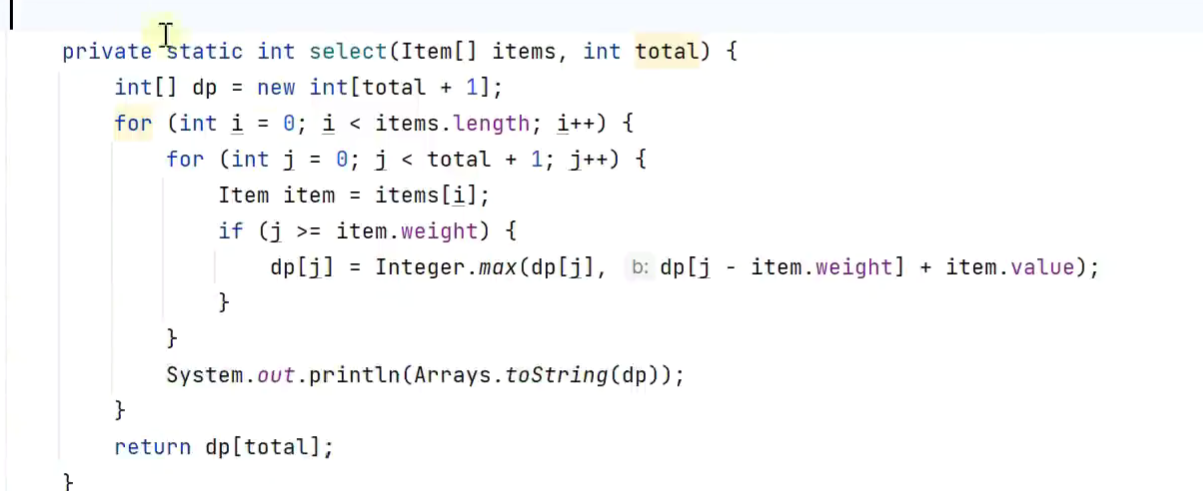
-
零钱兑换 动态规划

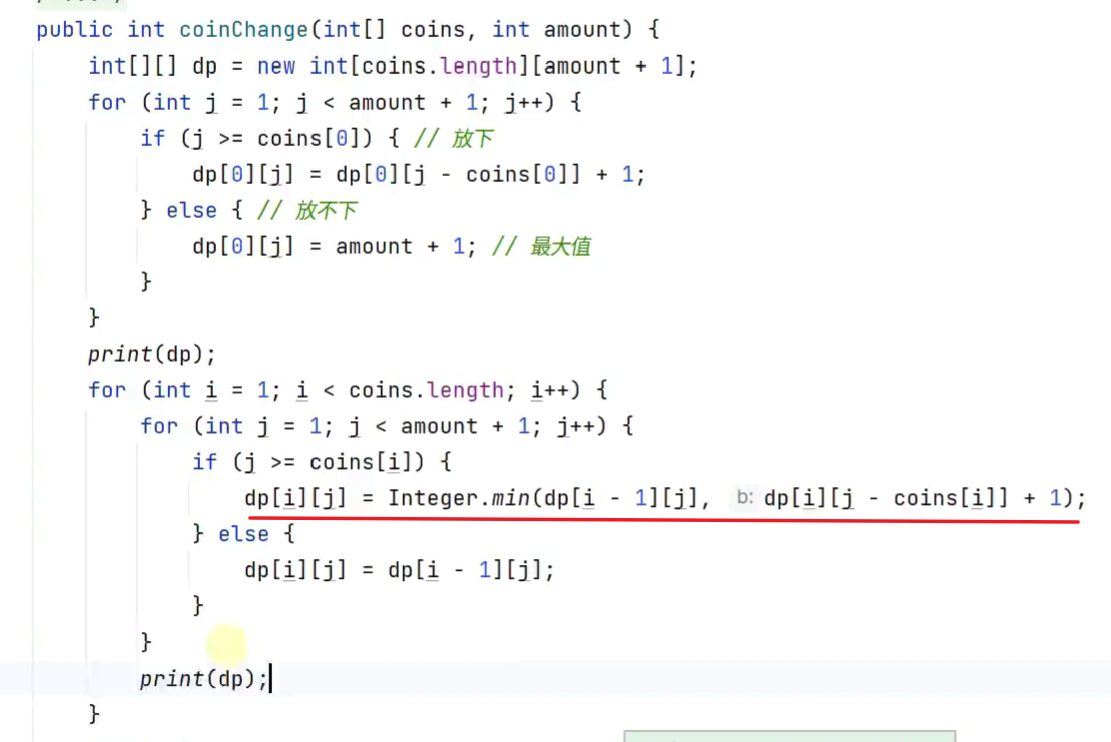
降维
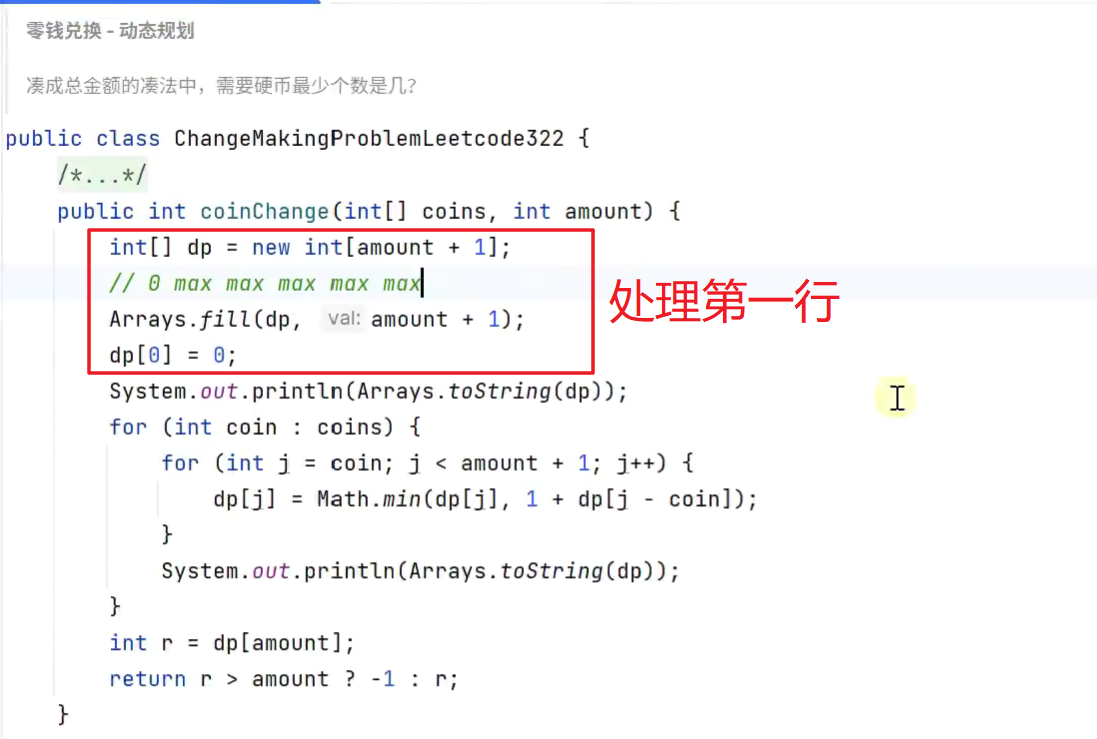
-
零钱兑换 所有兑法

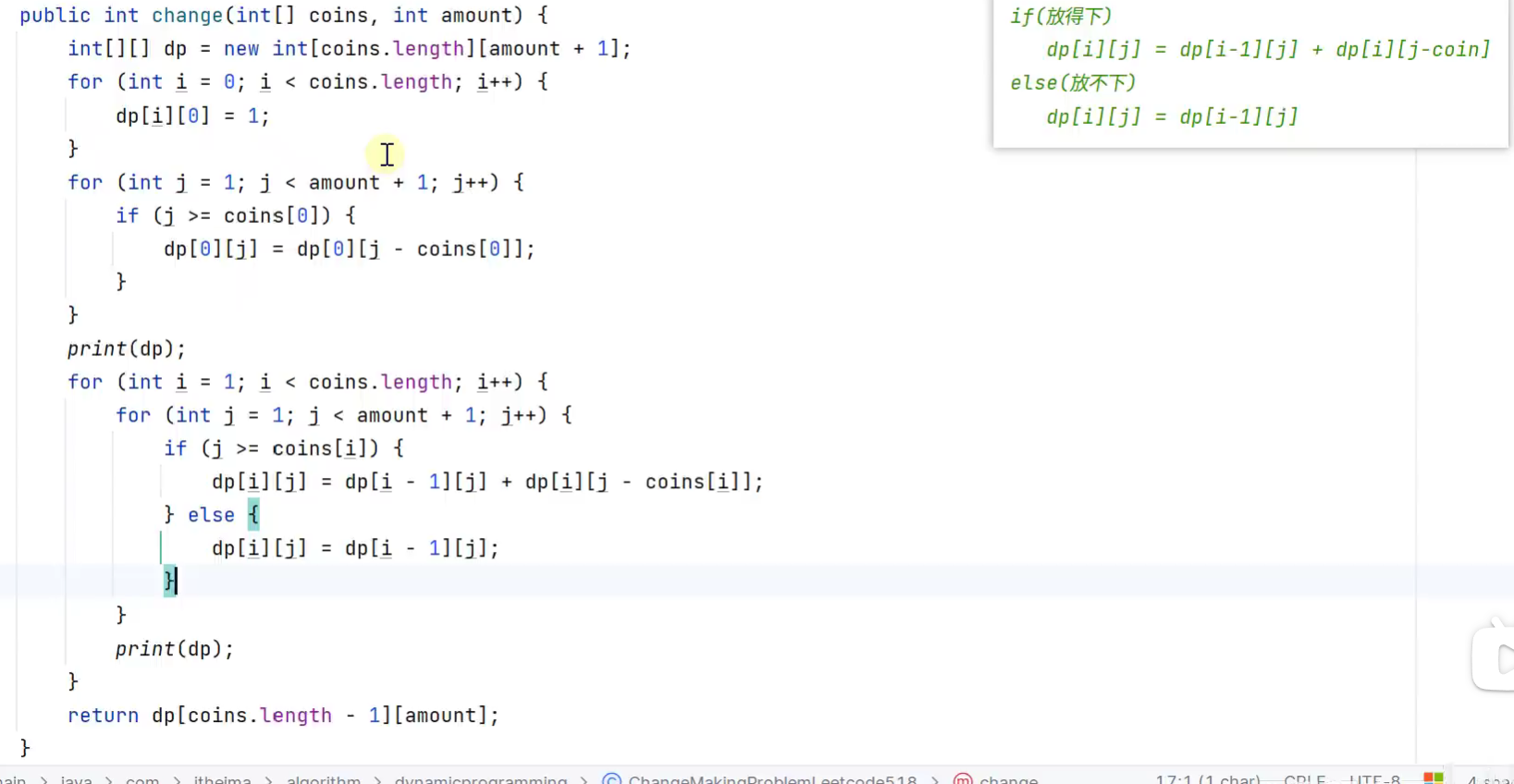
-
钢条切割问题

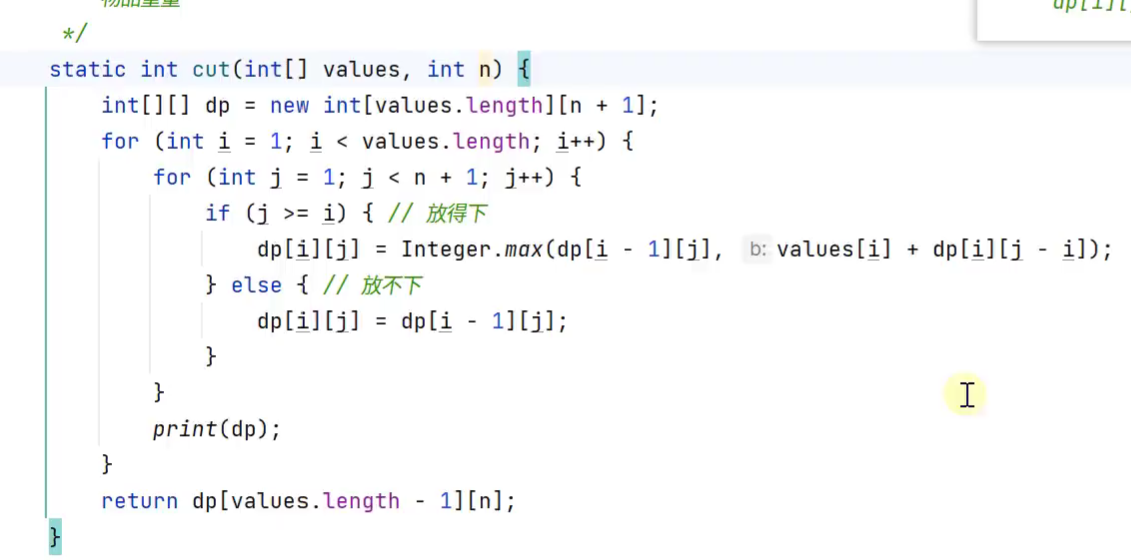
-
最长公共子串 动态规划

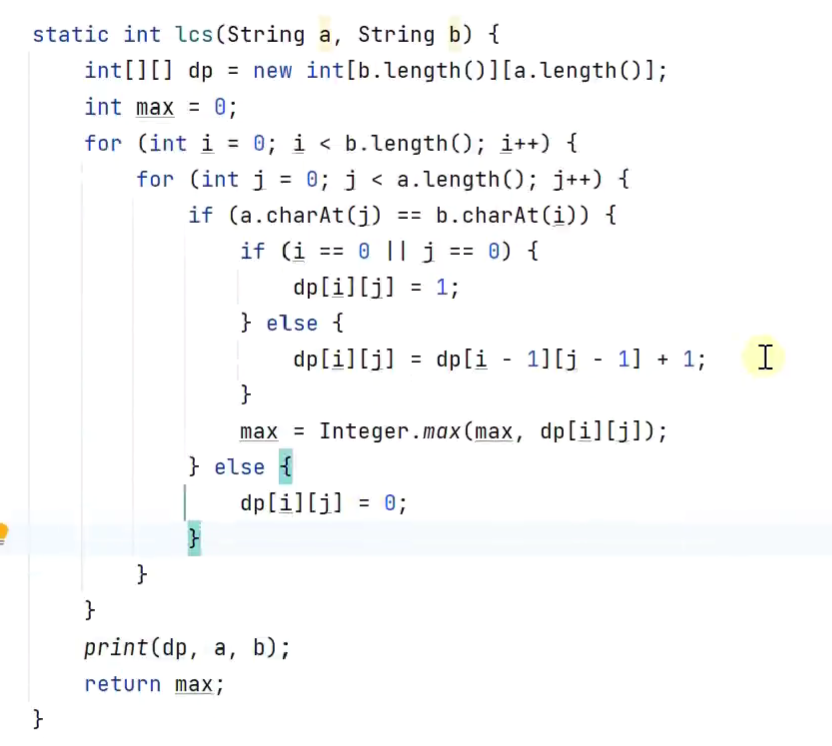
-
最长公共子序列



上面和左面中取大的
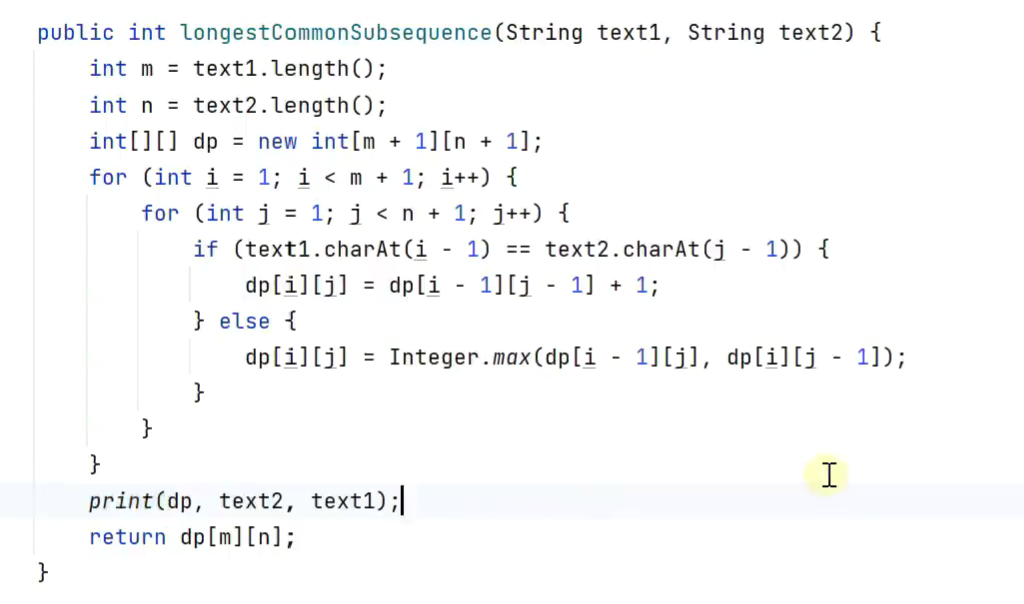
-
两个字符串的删除操作,删到相同
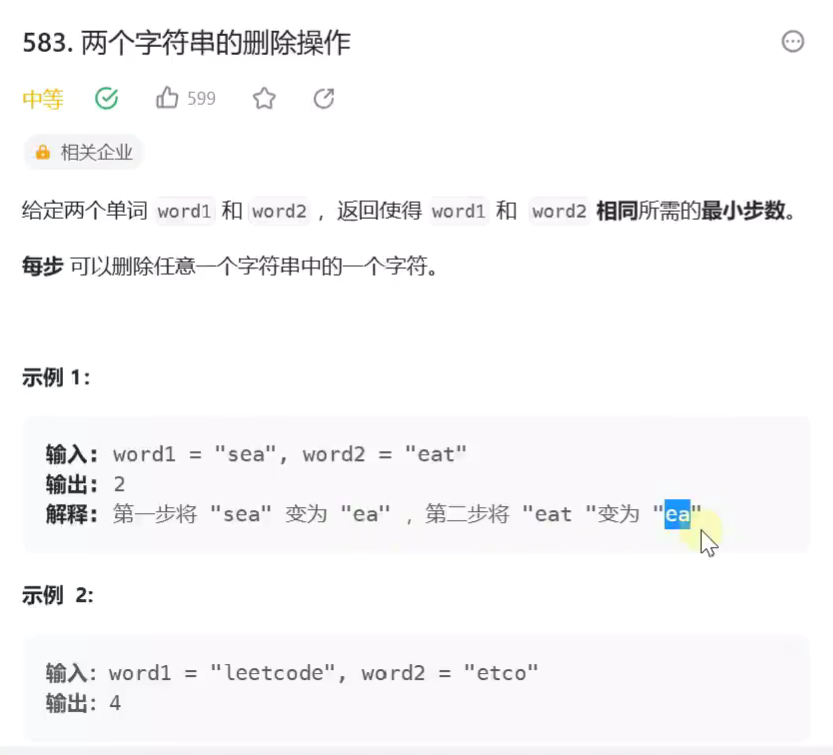
字符串1长度 + 字符串2长度 - 2*公共子序列长度 == 删除的长度
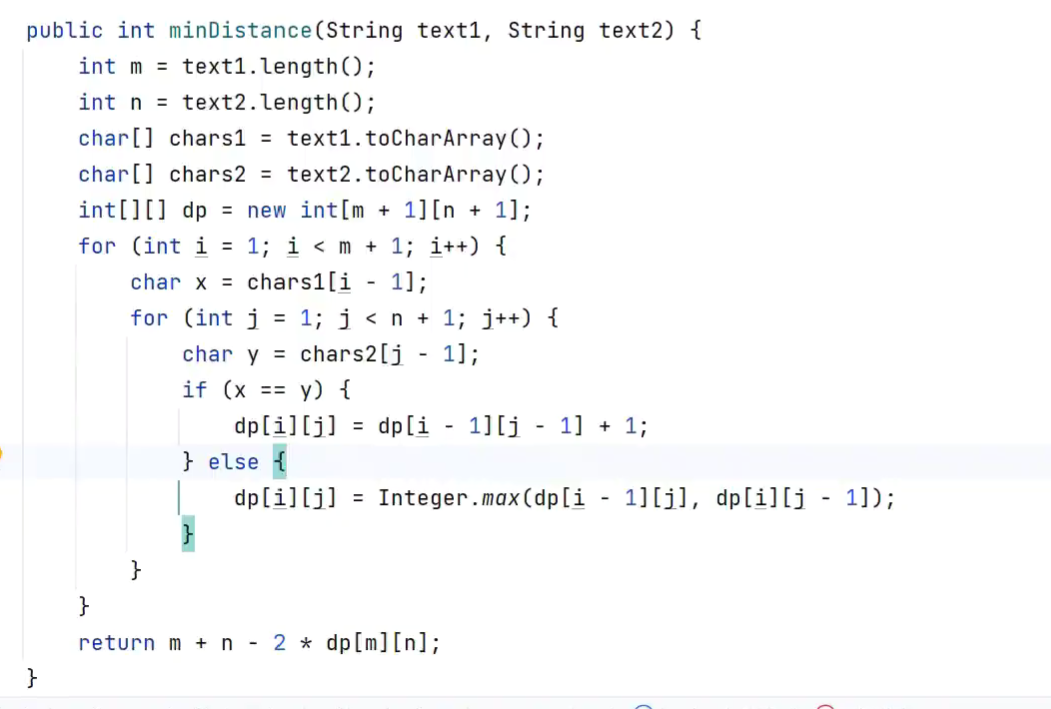
-
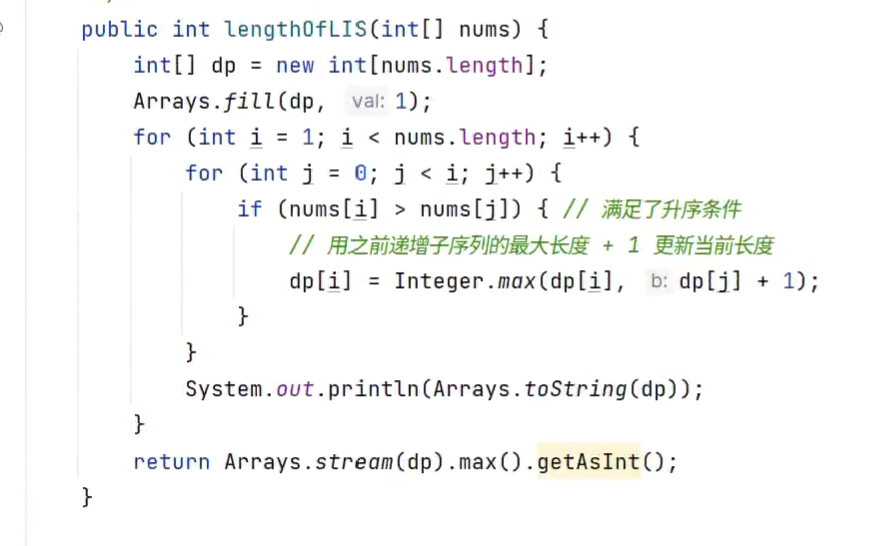
最长递增子序列

-
不同的二叉搜索树
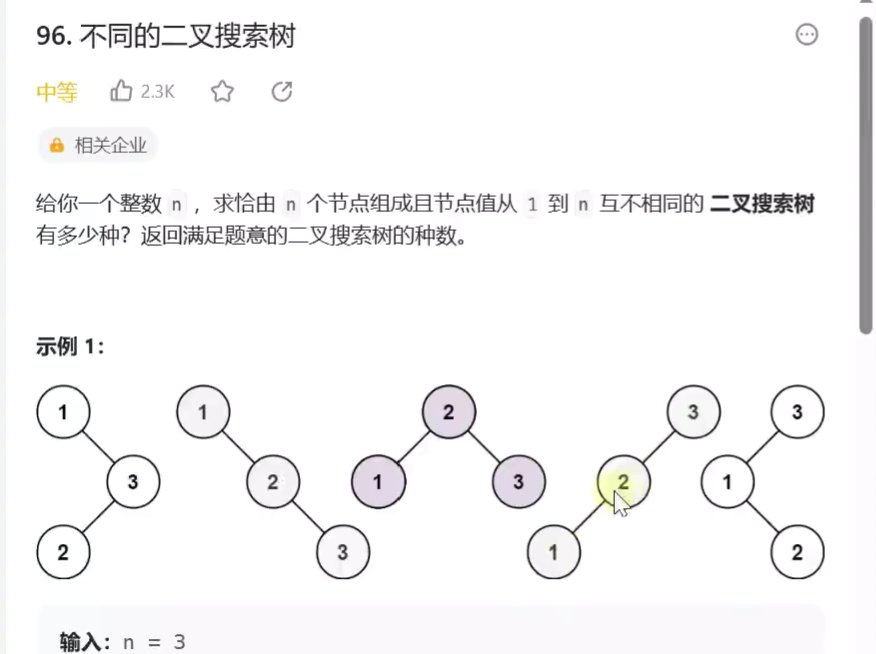
卡特兰数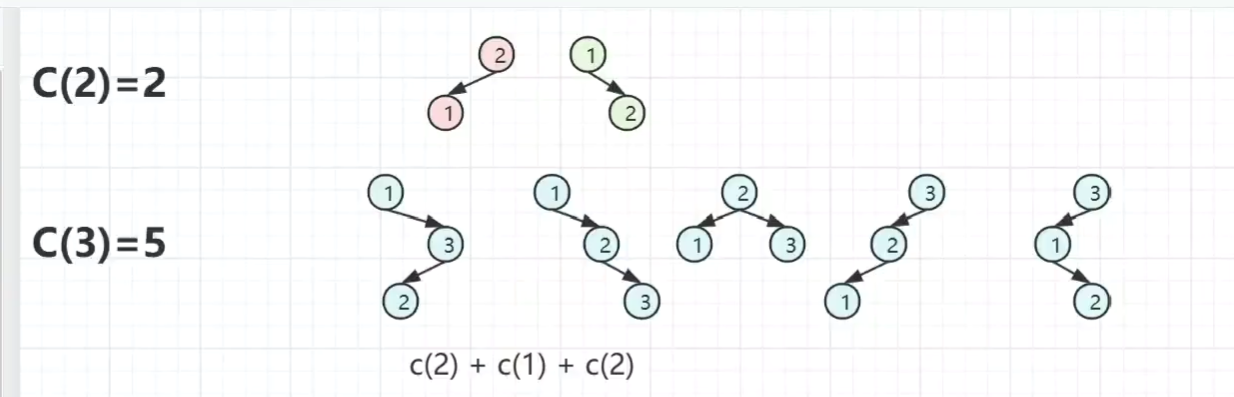
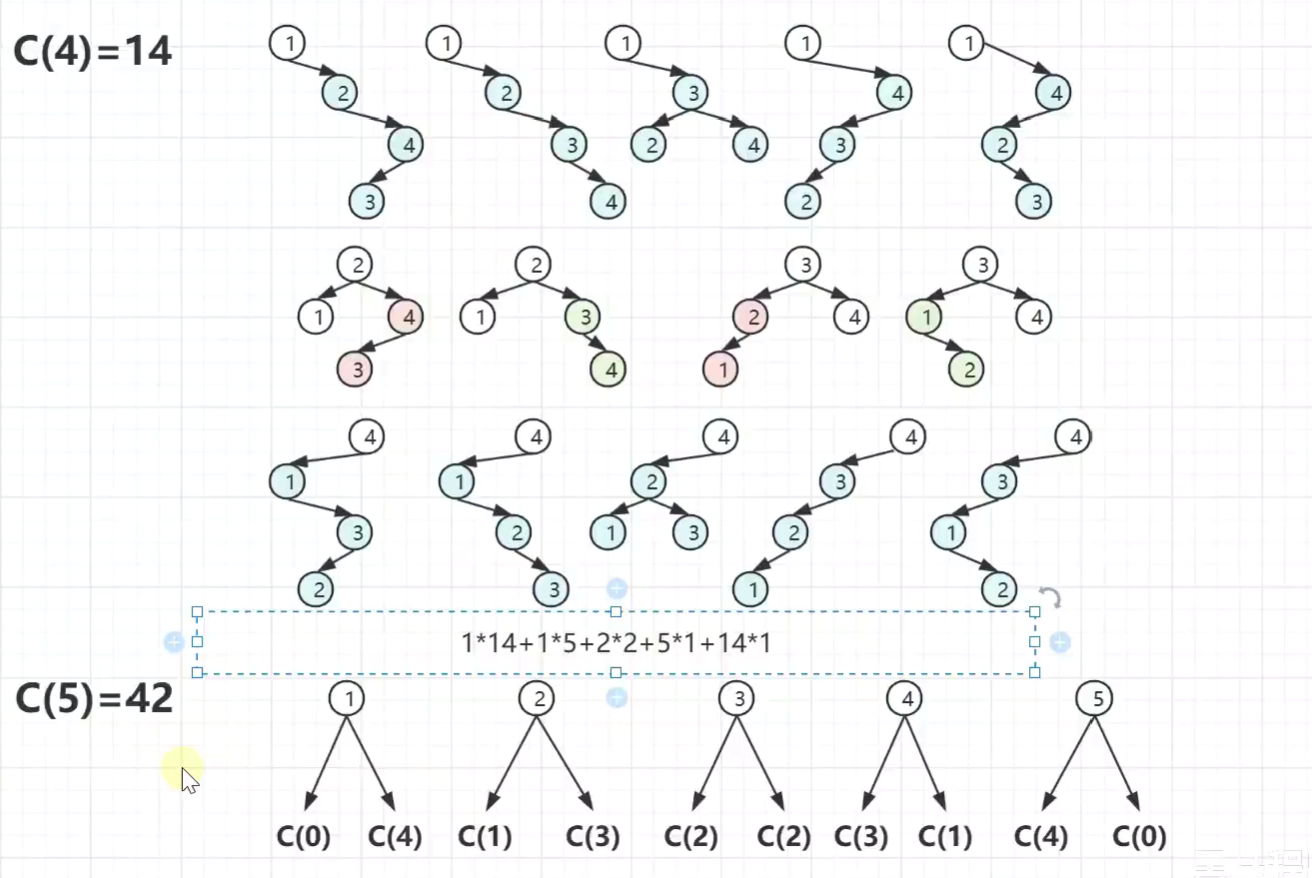
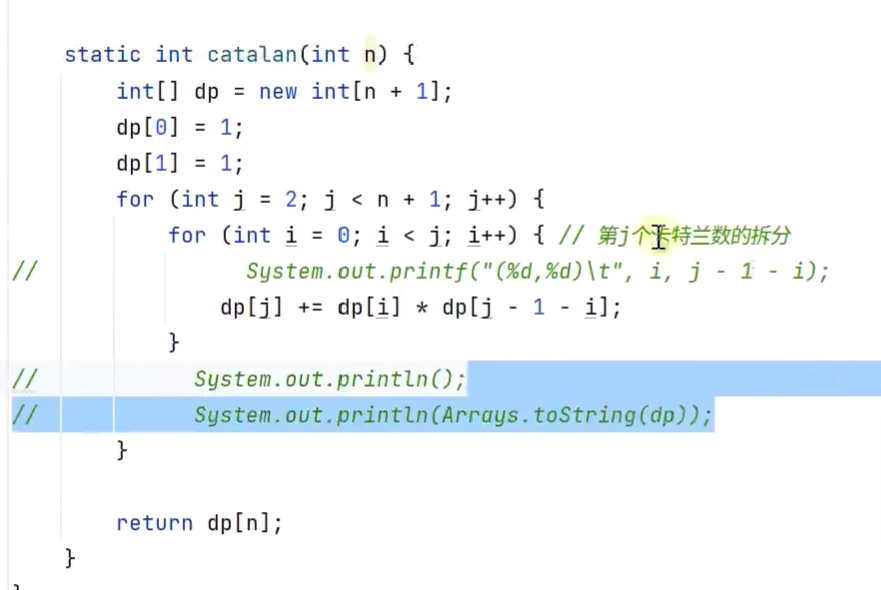
-
利用卡特兰数 求出战序列有多少种
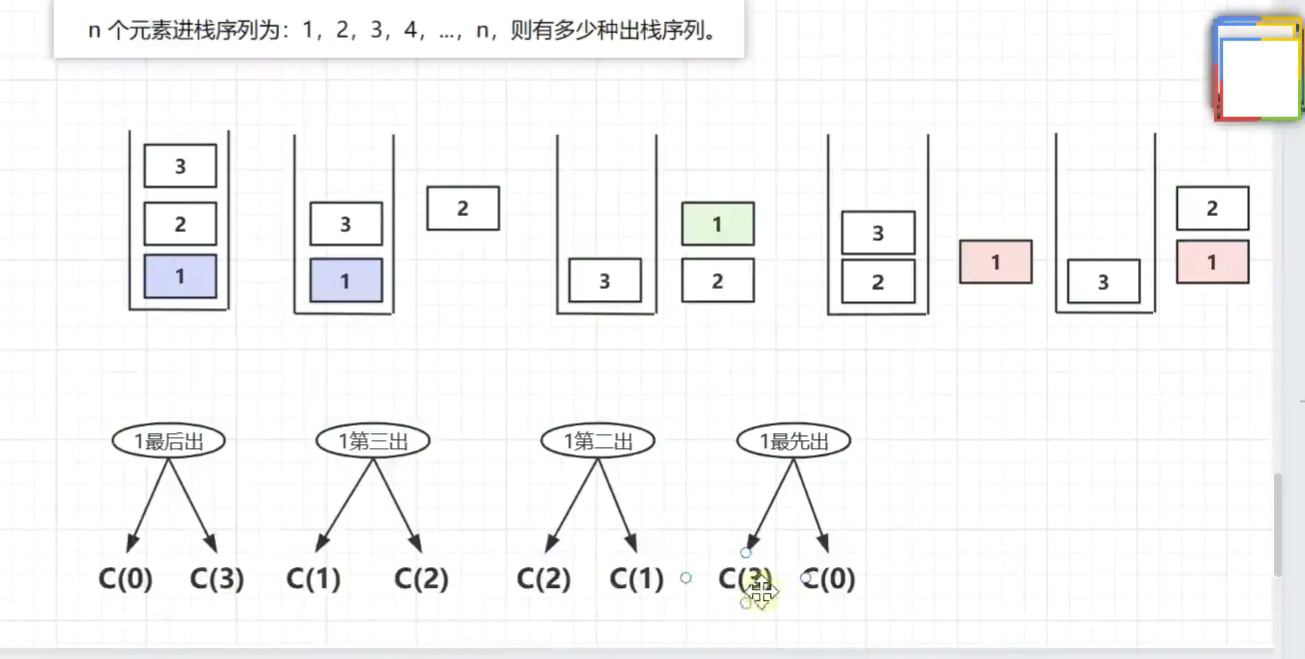
-
括号 生成
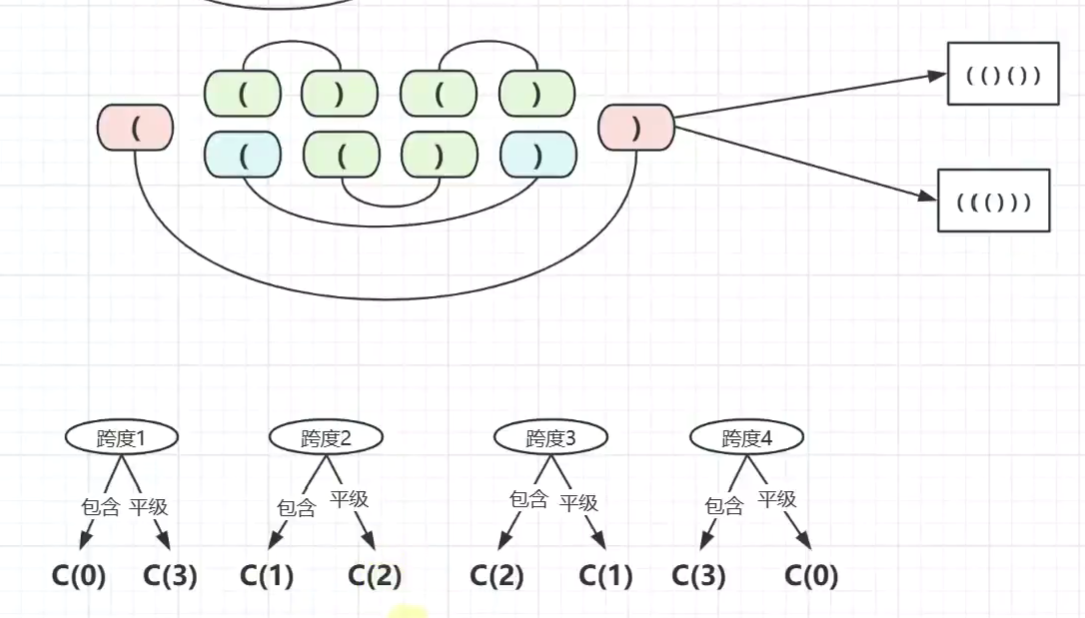
-
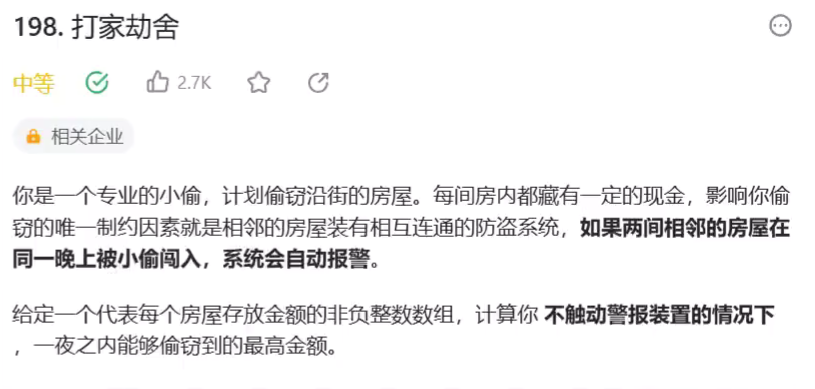
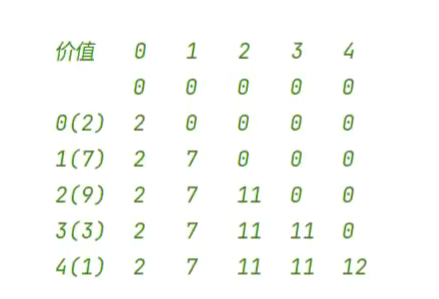
抢钱


-
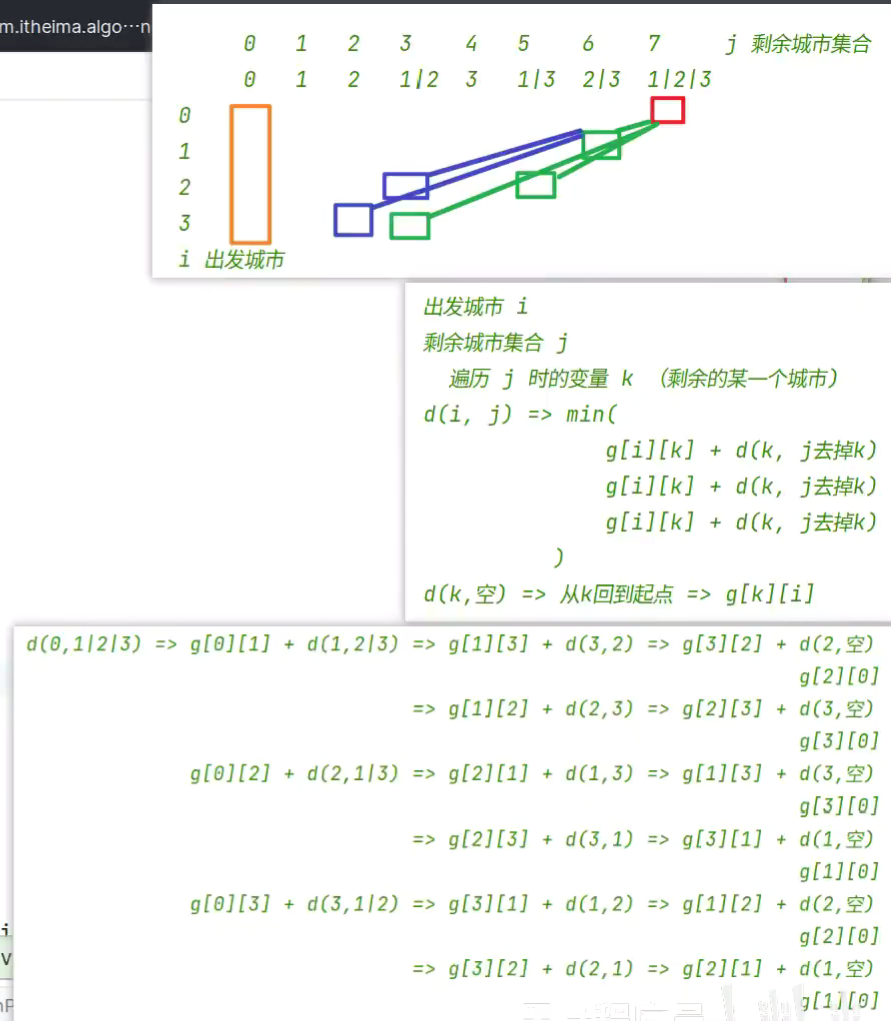
旅行商问题




-
分治


-
快速选择算法
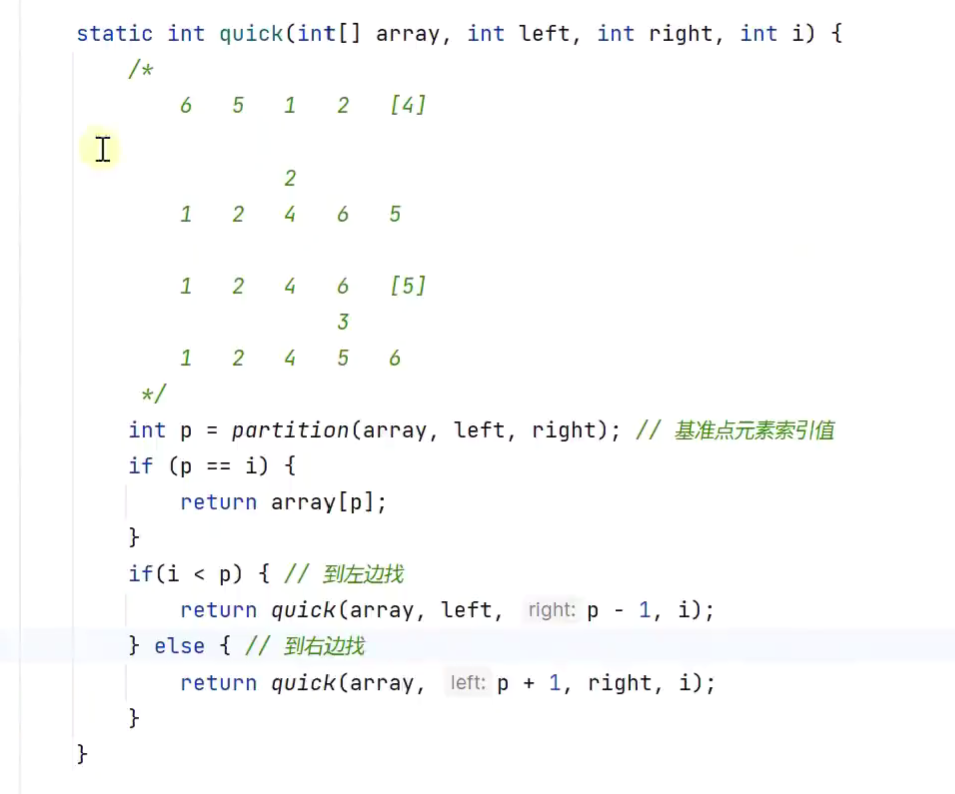
-
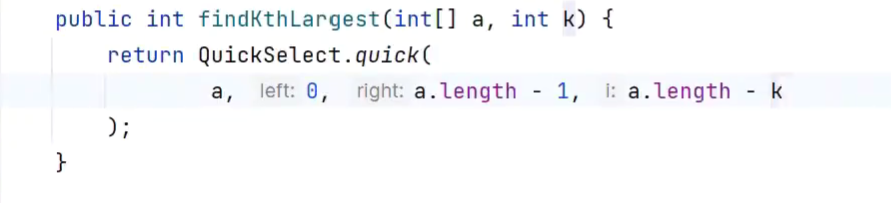
求数组中第K大的元素

利用快速选择算法 O(n)
-
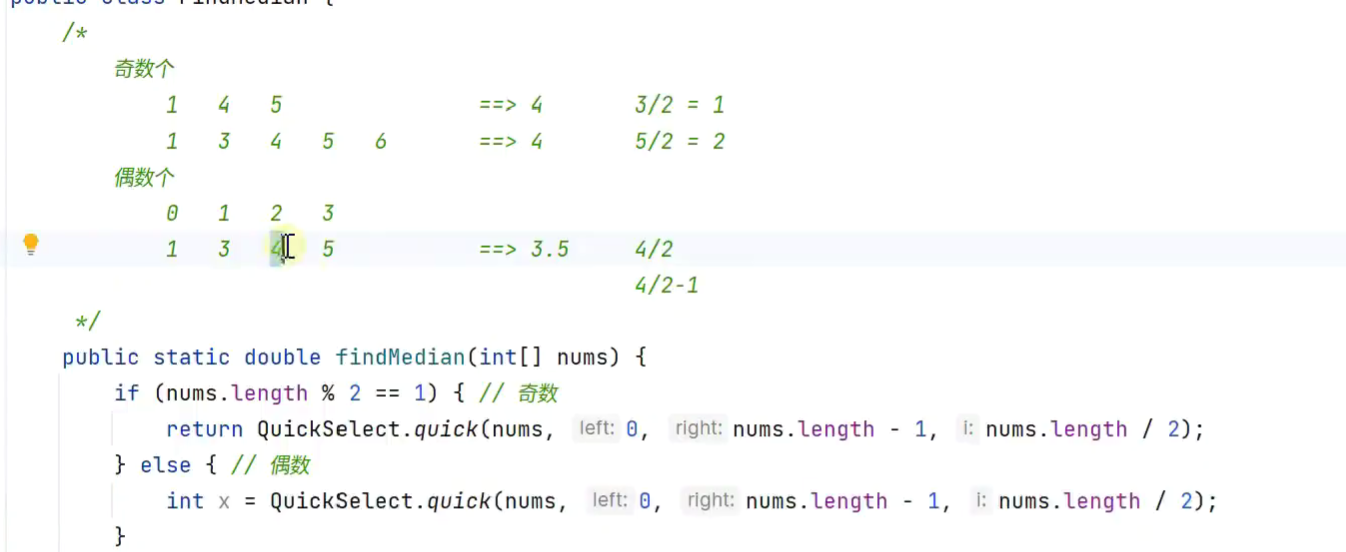
数组中位数
-
快速幂

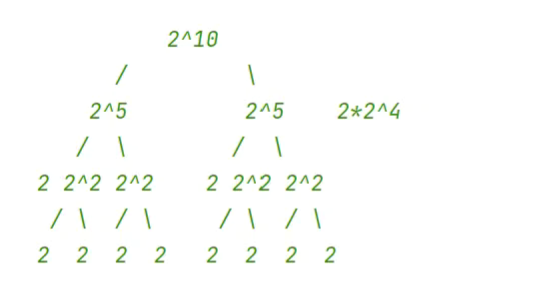
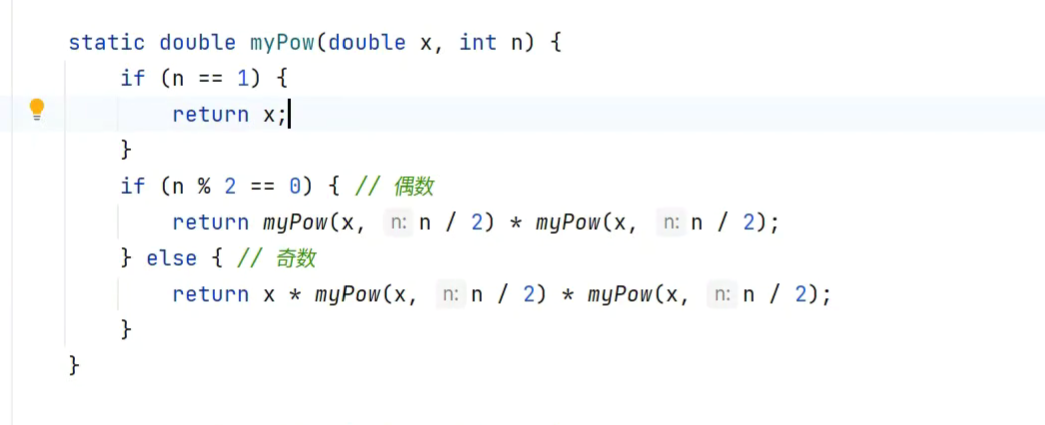
改进
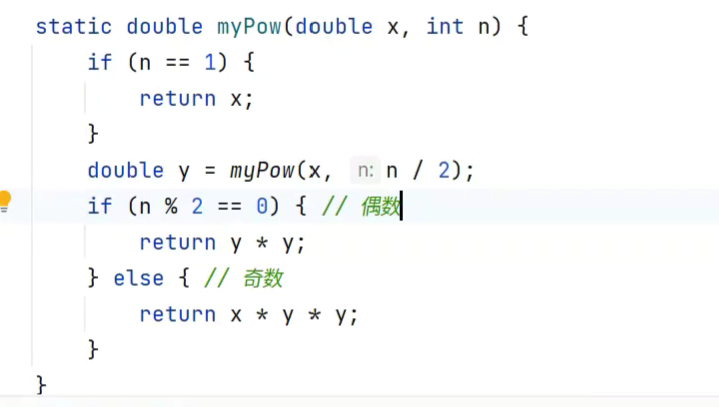
改进0的情况

改进负数次幂的情况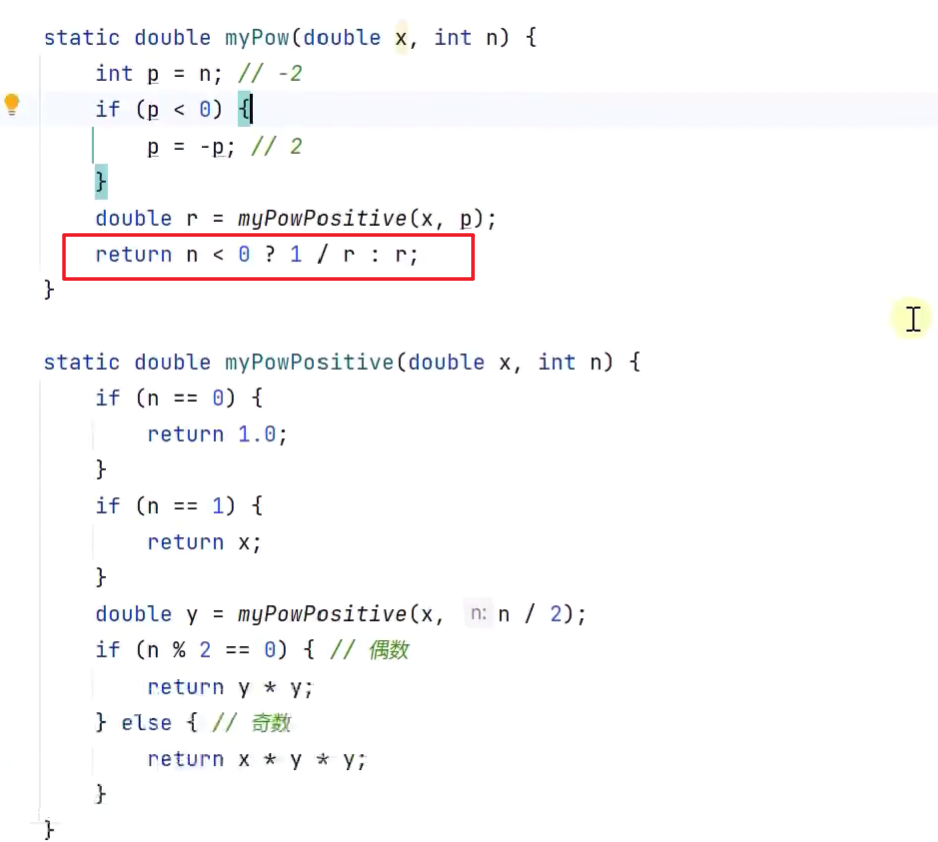
改进极限负值(Integer最小值)换成long就行
另一种判断奇偶的方法
与1按位与,通过判断最后一位
-
平方根整数部分

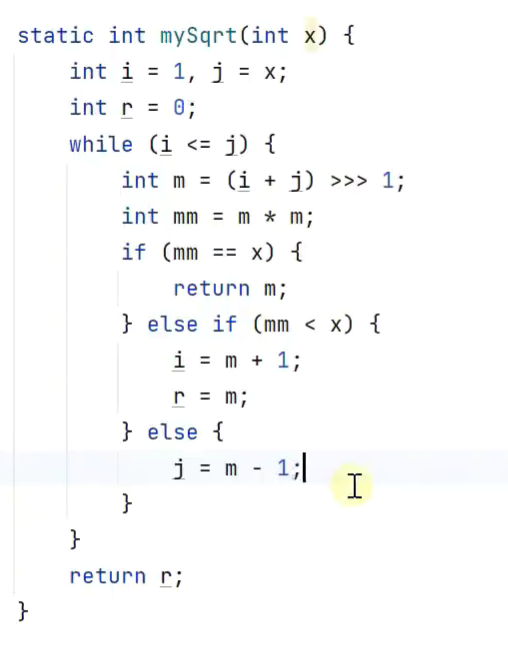
缺陷:大数容易越界
改进:改成除法
- 至少有k个重复字符的最长子串


逐步去除出现频率不符合要求的字符

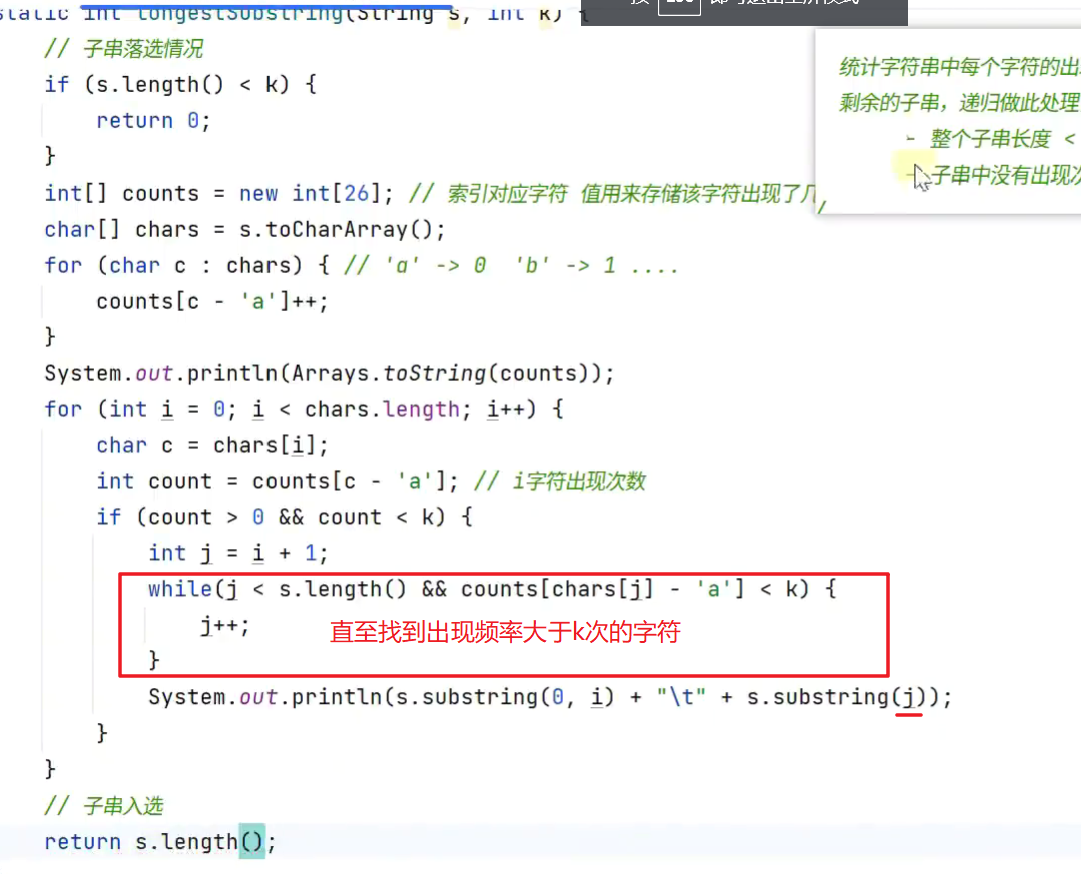
- 回溯

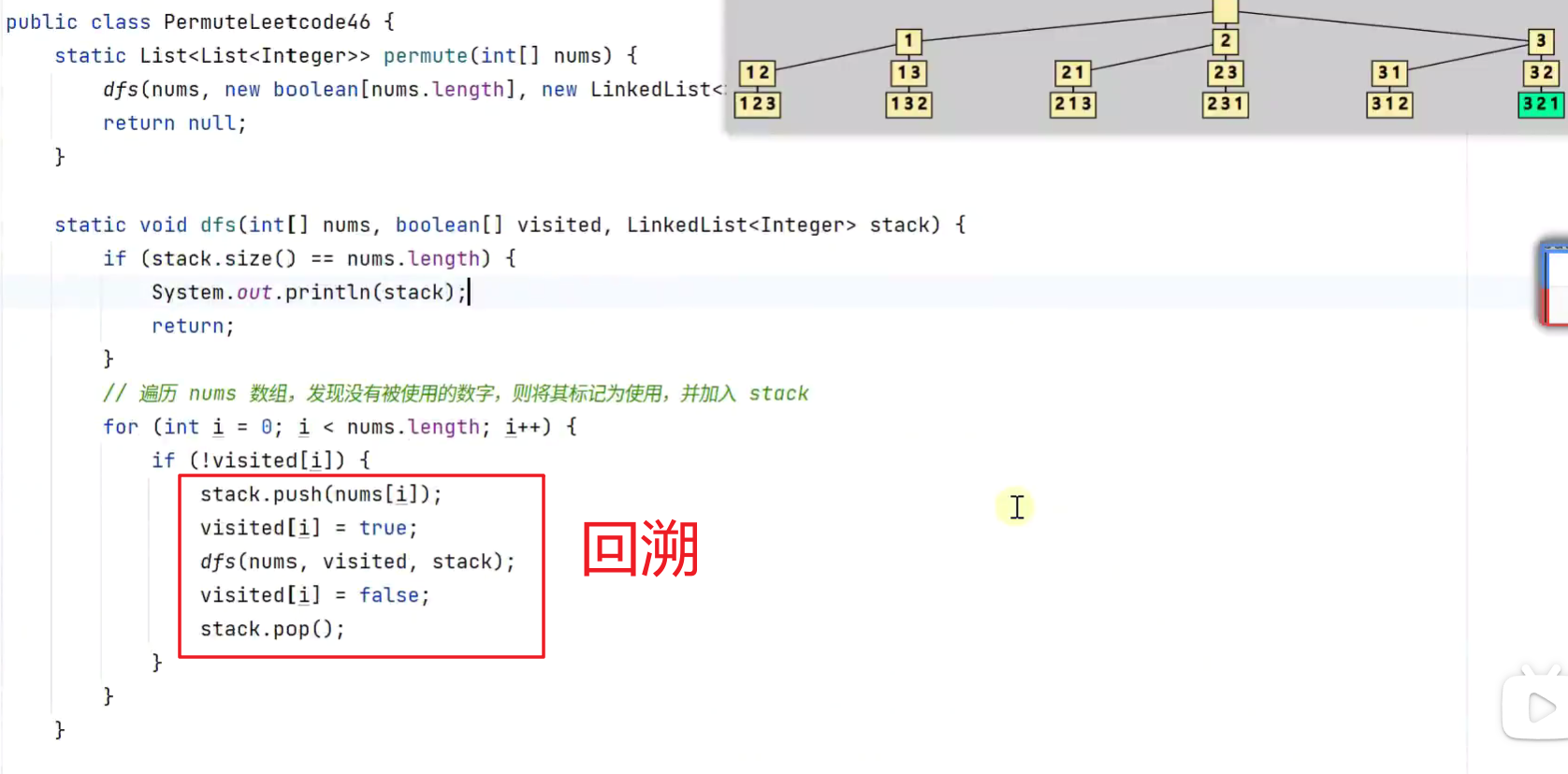
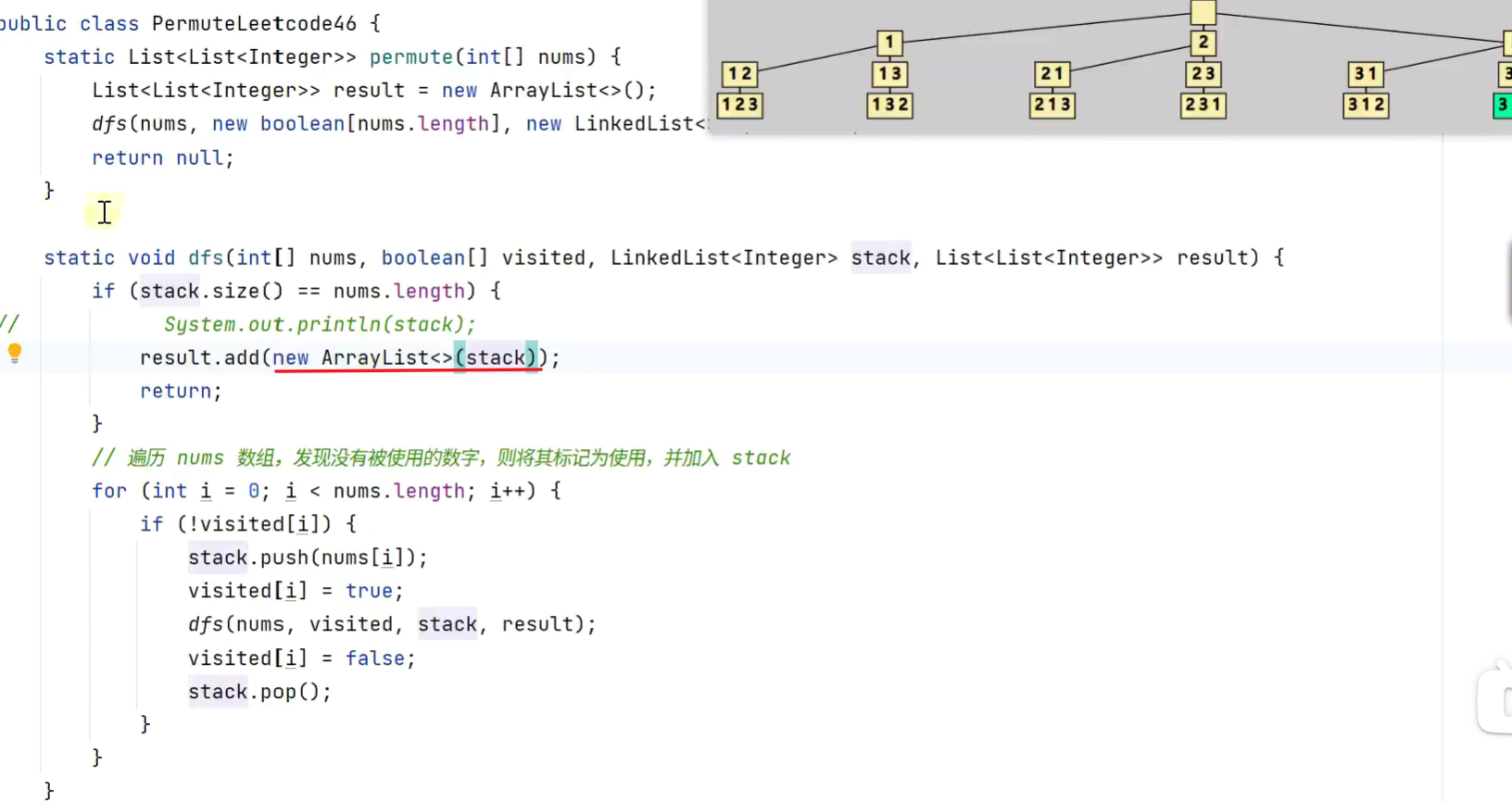
-
全排列II
去除重复的排列
剪枝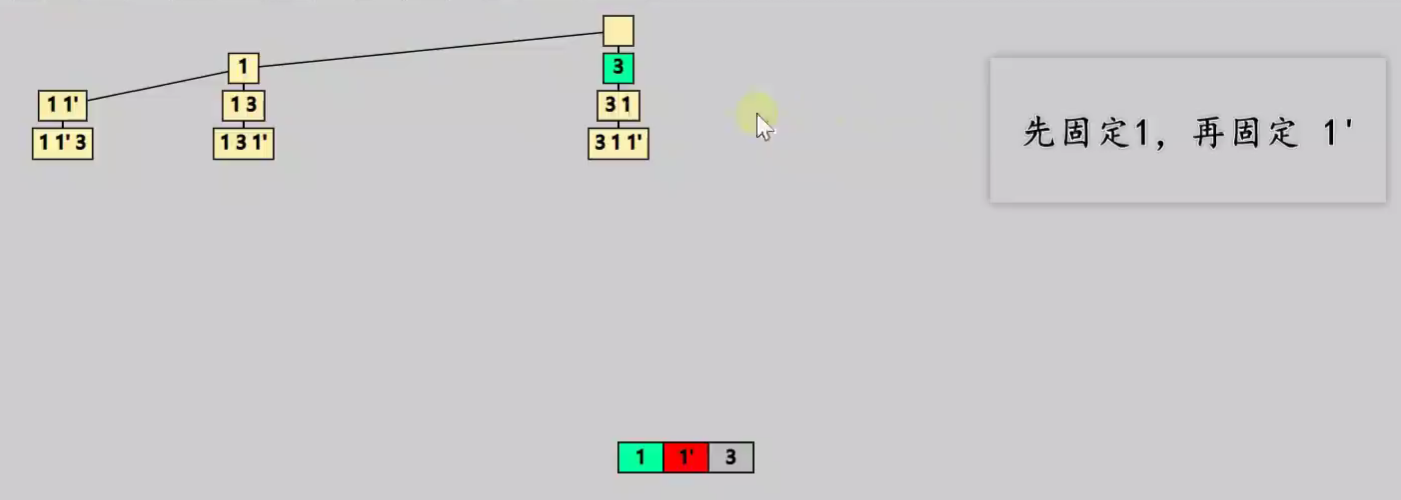
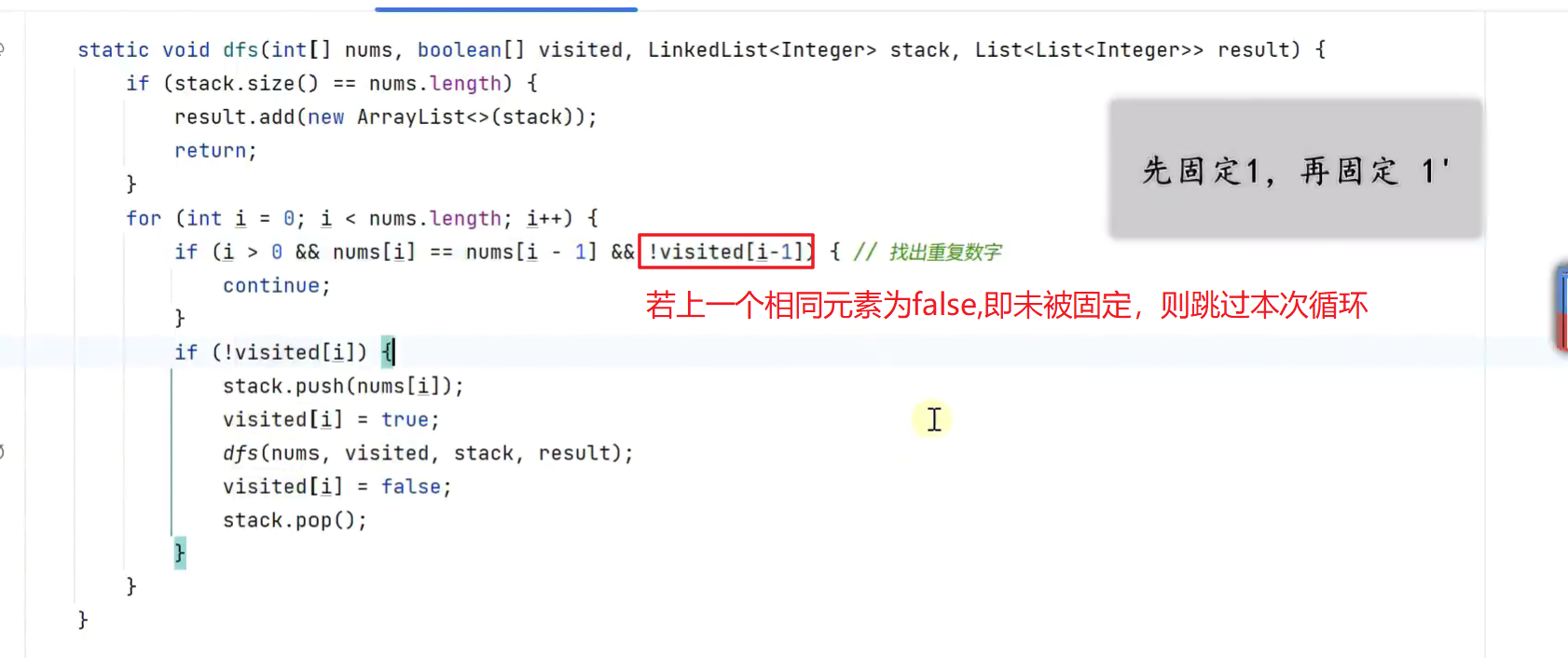
-
组合


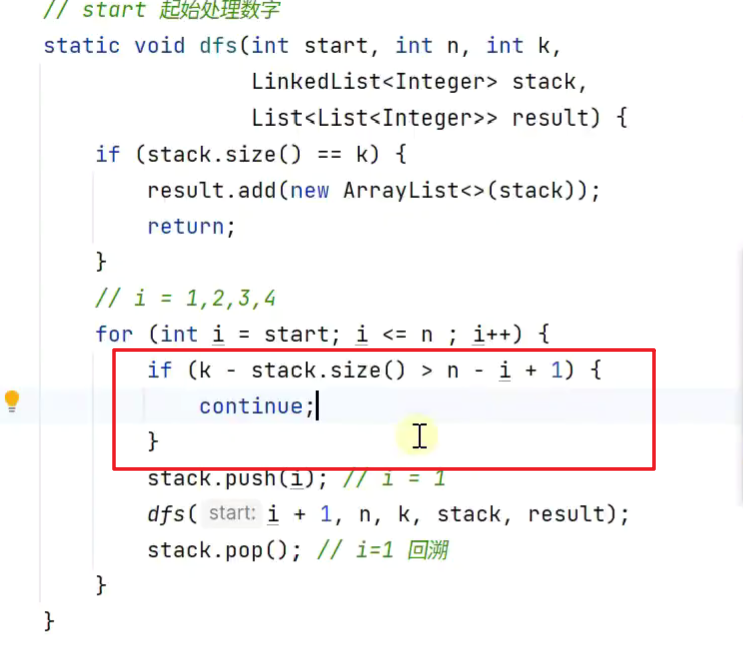
剪枝优化
把多余的显然之后都不符合条件剪掉
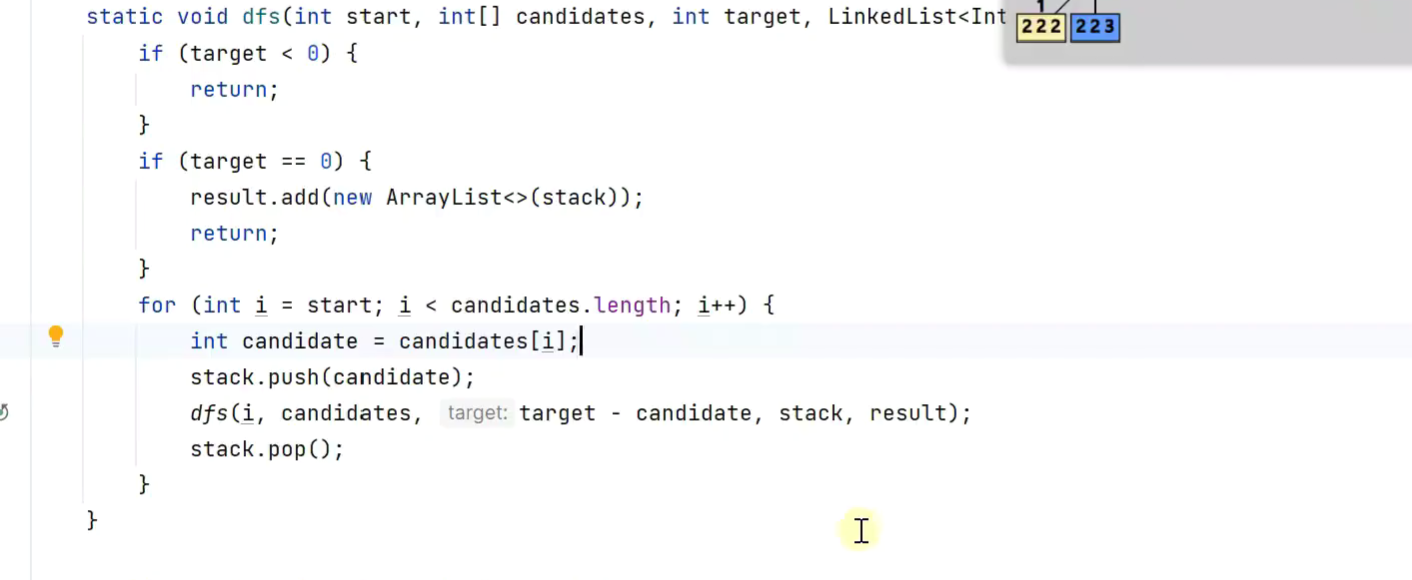
- 组合总和,类似零钱兑换
剪枝,优化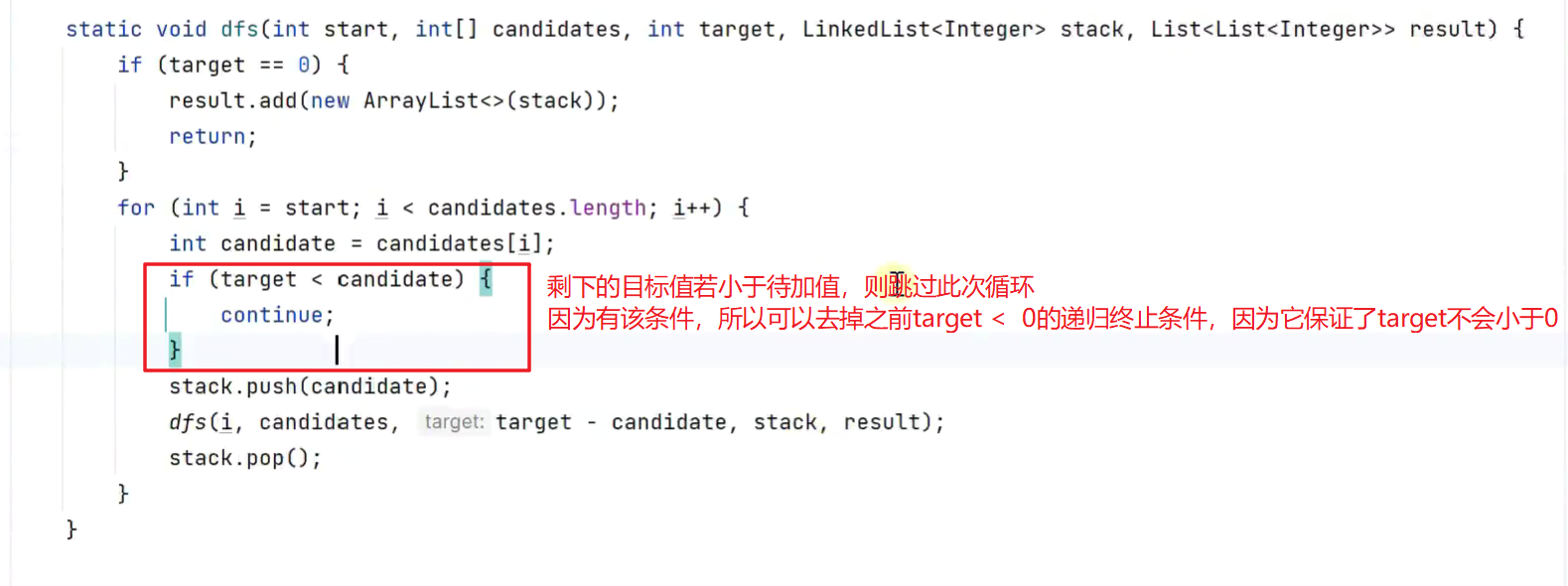

-
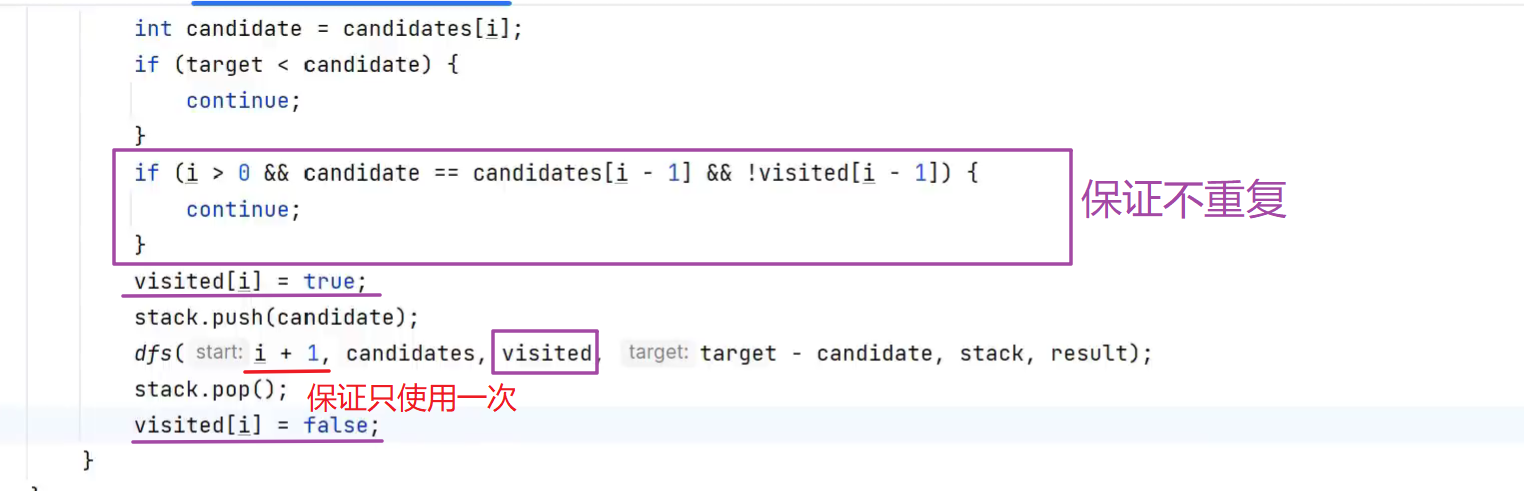
组合总和II
只能用一次,且不允许有重复
-
组合总和III
和组合比较类似
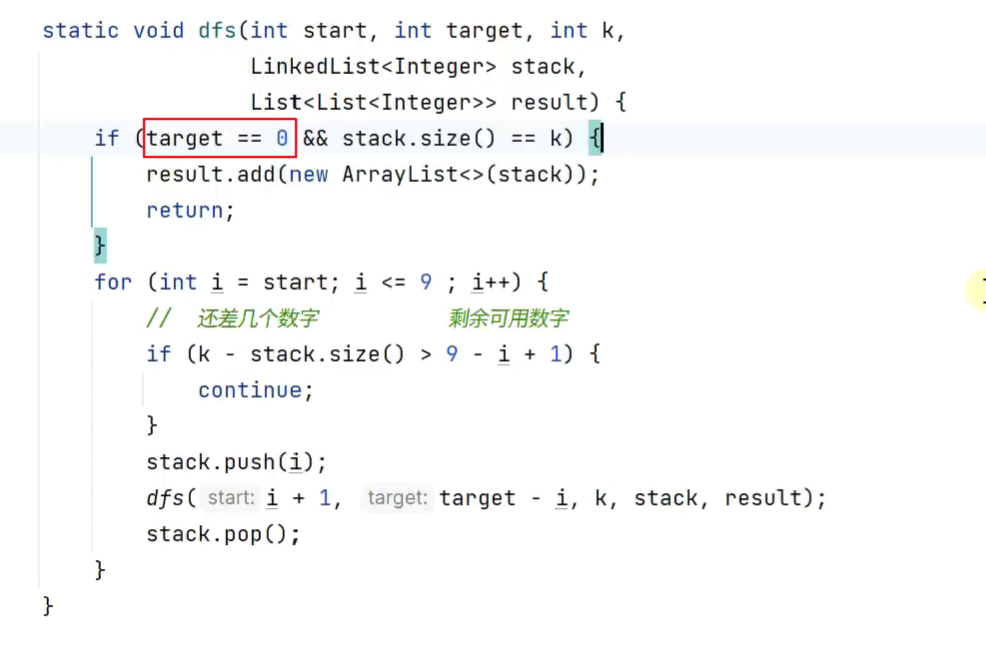
更有效的剪枝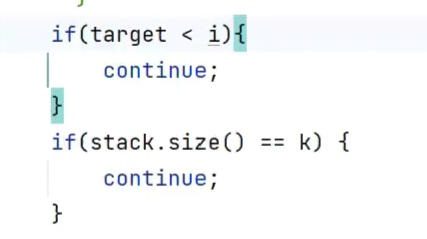
-
N皇后
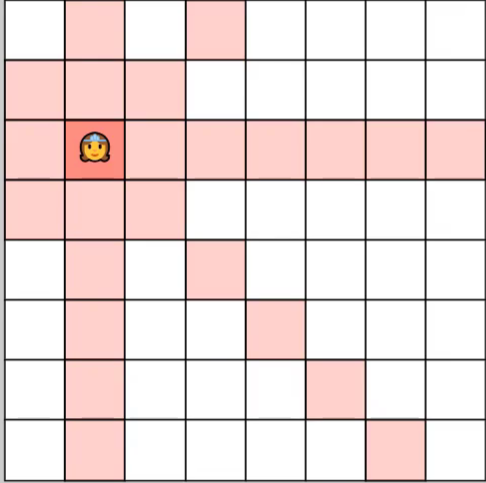
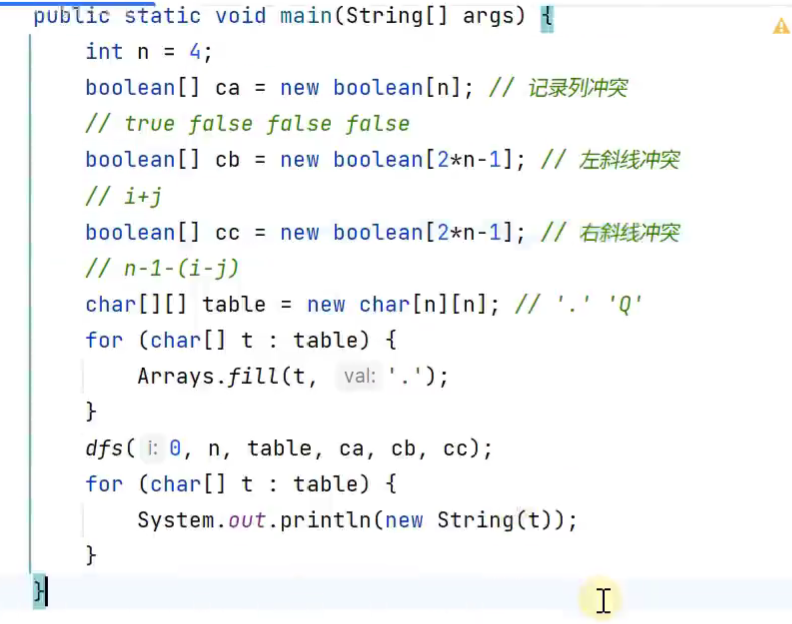
i为正在处理第几行
n为数组的维度,也是皇后的个数
一行一行尝试放皇后,每一行中对不同列进行尝试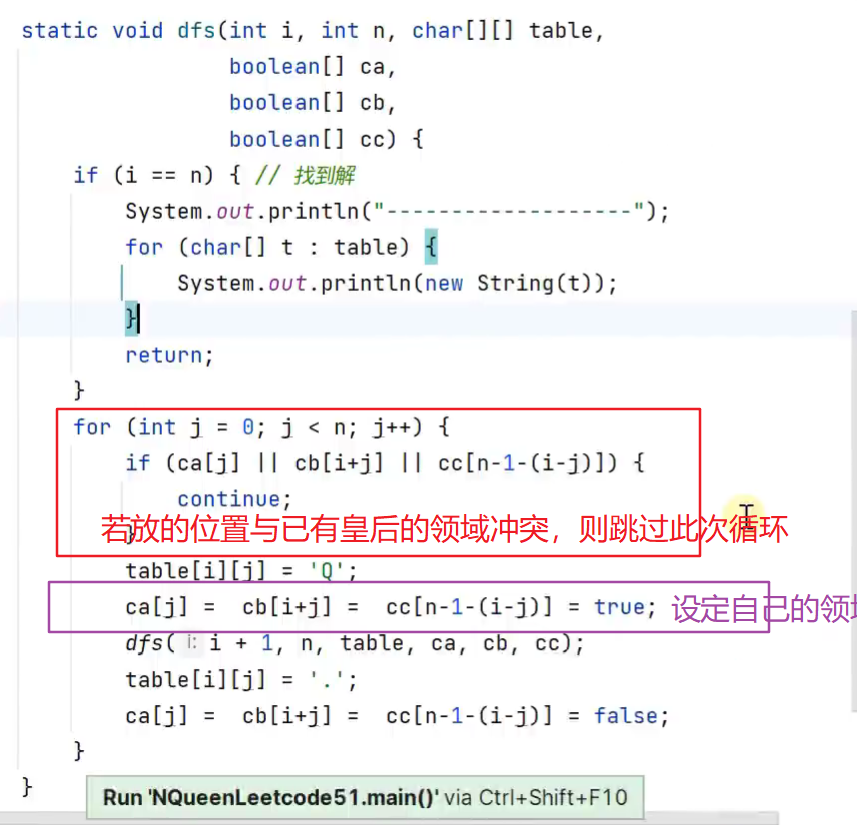
若递归失败,没地方可放,则恢复到递归之前的状态,
-
解数独
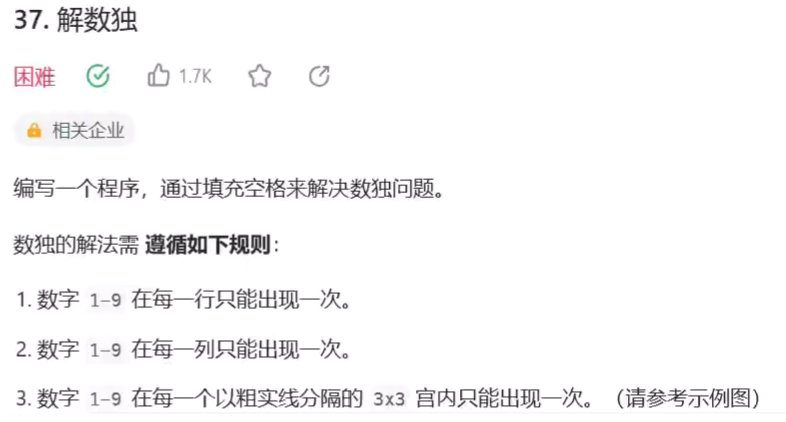


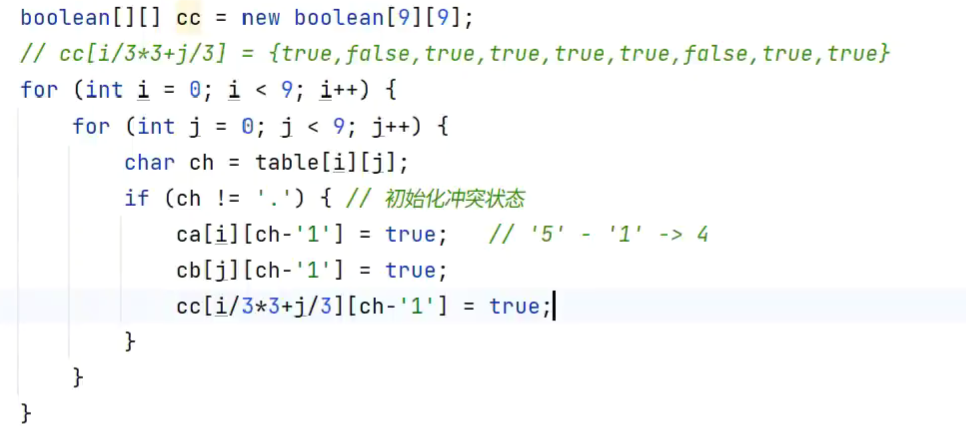


- ,
-