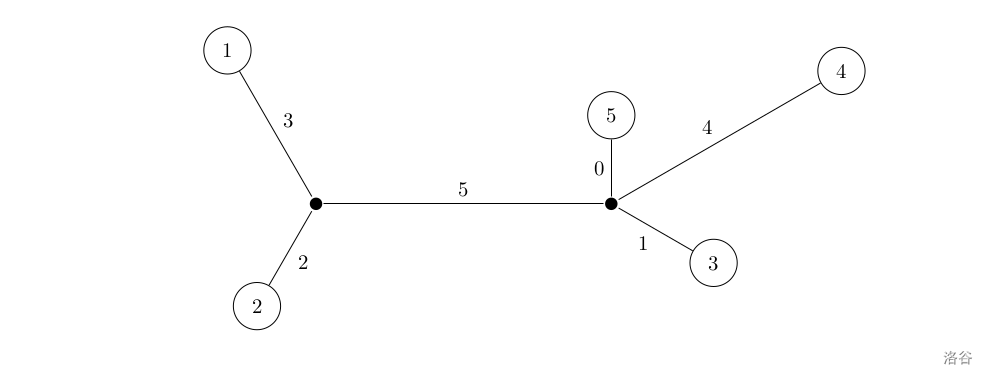
暑假集训D4 2023.7.27 补题

CF不上1400不改名 / 2023-07-28 / 原文

昨天做搜索专题真是太折磨了,总是想不到.今天比昨天稍微好一点,但也没好哪去.

H. P2504 [HAOI2006] 聪明的猴子

这题虽然最后 $AC$ 了,但是中途做了好几种方法都没成功.

首先是把点的坐标转化成距离,给出来的点两两组合就好了.注意是双向的. $i \rightarrow j$ $\ \ \ $ $j \rightarrow i$

然后就是求解过程了

首先想用类似于 $dijkstra$ 的方法做的.

if(dist[j]>w[i])
{
	dist[j] = w[i];
	q.push({dist[j],j});
}

先求出到点 $i$ 的最短的边权 ,记为 $dist[i]$ ,然后对所有点的权 $dist$ 取 $\max$ .

double res = -1;
for(int i =1;i<=n;i++)
{
	res = max(res,dist[i]);
}
return res;

很不幸的 $WA$ 了,后面有时间写对拍改一下.

本来想的是,对于一个点 $j$ ,如果他能到其他任意的一个点,最短的一条边边权为 $w$ ,就记为 $dist[j]$ ,然后统计所有点的 $dist$ ,取 $\min$ 作为答案.比如 $1$ 有边直接连接到 $2\ 3\ 4$ 三个点, 距离分别为 $4\ 5\ 2$,只要青蛙能跳 $2$ 的距离,那么青蛙就可以从 $4 \rightarrow 1$ , 然而这可以被 $hack$ 掉:

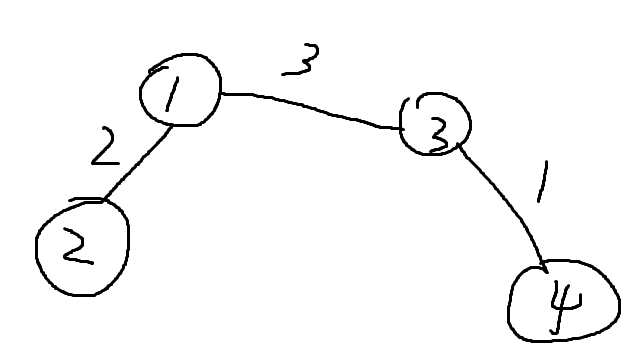
青蛙想觅食必须得通过 $1 \rightarrow 3$ 这条边. 因此最短距离必须是3

正解是用 $Kruskal$ 算法. $n$ 个点连通后最大的那条边即为答案

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<iostream>
#include<algorithm>
#include<math.h>
#include<queue>
#define endl '\n'
using namespace std;
const int N = 2e6+10;
double w[N];
struct edge
{
	int a,b;
	double c;
	bool operator<(edge &b)&
{
	return c<b.c;
}
}e[N];
int idx ;
int f[N];
int find(int x)
{
	if(x!=f[x]) f[x] = find(f[x]);
	return f[x];
}
typedef pair<double,int> PII;
int n;
PII node[N];
double dis(PII a,PII b)
{
	return sqrt((a.first-b.first)*(a.first-b.first)+(a.second-b.second)*(a.second-b.second));
}
double mouse[N];
int m;
int main()
{
	
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin>>m;
	for(int i= 1;i<=m;i++)
	{
		cin>>mouse[i];
	}
	sort(mouse+1,mouse+m+1);
	cin>>n;
	for(int i = 1;i<=n;i++)
	{
		f[i] = i;
	}
	
	for(int i =1;i<=n;i++)
	{
		int x,y;
		cin>>x>>y;
		node[i]={x,y};
	}
	for(int i =1;i<=n;i++)
	{
		for(int j=i+1;j<=n;j++)
		{
			e[idx++]= {i,j,dis(node[i],node[j])};
		}
	}
	sort(e,e+idx);
	double max_dis = -1;
	for(int i=0;i<idx;i++)
	{
		int a = e[i].a;
		int b = e[i].b;
		int pa = find(a);
		int pb = find(b);
		if(pa!=pb)
		{
			f[pa] = pb;
			max_dis = max(max_dis,e[i].c);
			//cout<<a<<" "<<b<<" "<<e[i].c<<endl;
		}
	}
	
//	cout<<max_dis<<endl;
	int pos = ((lower_bound(mouse+1,mouse+m+1,max_dis)-mouse-1));
	//cout<<pos;
	cout<<m-pos;
	
	return 0;
}