【学习笔记】【数学】概率与期望

sonnety-v0cali0d-kksk / 2023-07-21 / 原文

前言

如果不小心发表出去了那么大概率是我手滑点错了，没有更新完那就是我也在学，有问题请@我。

概率这个说到底和动态规划挂钩，逃离不了动态规划，而概率又给动态规划添了一层难度。

所以这篇博客应该重点不会在基础知识，可能后期会发展成杂题乱写的地步（？）

然后是我们的宣言：概率期望狗都不做！！！！！

基础知识：

互斥事件：事件 \(A\) 和 \(B\) 的交集为空， \(A\) 与 \(B\) 就是互斥事件，也叫互不相容事件。也可叙述为：不可能同时发生的事件。如 \(A∩B\) 为不可能事件（ \(A\bigcap B=\varnothing\) ），那么称事件 \(A\) 与事件 \(B\) 互斥，其含义是：事件 \(A\) 与事件 \(B\) 在任何一次试验中不会同时发生。

对立事件：对立事件是指其中必有一个发生的两个互斥事件。

独立事件：所谓独立事件就是某事件发生的概率与其它任何事件都无关，用集合的概念解释即集合之内所有事件发生的可能性范围互不相交。

- 前言
概率
- 条件概率公式
  - 定义：
  - 公式：
  - 乘法公式：
  - 乘法公式的推广：
- 全概率公式
  - 定义：
  - 公式：
  - 例题：
- 贝叶斯公式
  - 定义
  - 公式
  - 例题：
- 杂题乱写(?)
  - POJ3071 Football

概率

条件概率公式

定义：

条件概率：

在另外一个事件 \(B\) 已经发生的情况下，事件 \(A\) 发生的概率叫做 \(A\) 对 \(B\) 的条件概率。记作 \(p(A|B)\) ，易证\(p(AB)=p(A|B)p(B)\) ，若 \(p(A|B)==p(A)\) 则称事件 \(A\) 与事件 \(B\) 相互独立。

公式：

\[ \begin{aligned} p(A|B)=\frac{p(AB)}{p(B)} \end{aligned} \]

乘法公式：

由条件概率公式可得：

\[ \begin{aligned} p(AB)=p(A|B)p(B)=p(B|A)p(A) \end{aligned} \]

乘法公式的推广：

对于任何一个正整数 \(n>=2\) ，当 \(p(A_1A_2……A_{n-1})>0\) 时，有：

\[ \begin{aligned} p(A_1A_2……A_{n-1})=p(A_1)p(A_2|A_1)p(A_3|A_1A_2)……p(A_n|A_1A_2……A_{n-1}) \end{aligned} \]

全概率公式

定义：

完备事件组：

若事件 \(A_1,A_2,……,A_n\) 满足：

\(A_i \bigcap A_j==\varnothing\)，\(i\neq j\)
\(A_1 \bigcup A_2 \bigcup A_3 \bigcup …… \bigcup A_n==\Omega\)

则称这些事件是完备事件组。

(也称事件组 \(A_1,A_2……A_n\) 是样本空间 \(\Omega\) 的一个划分)

公式：

设 \(B_1,B_2,……,B_n\)是样本空间 \(\Omega\) 的一个划分， \(A\) 是任一事件，则：

\[ \begin{aligned} P(A) =\sum_{ i = 1 }^{ n } P(B_i)P(A|B_i) \end{aligned} \]

证明见图：

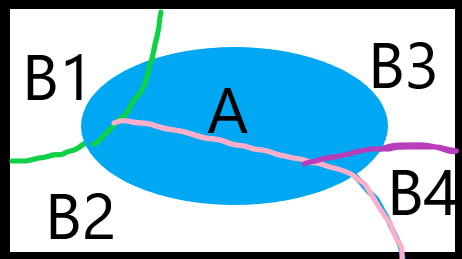
整个矩形为样本空间，蓝色椭圆是事件 \(A\).

显然 \(P(B_i)P(A|B_i)\) 等于 \(B_i\) 区域的那一块蓝色。

全概率公式将较难计算的事件 \(A\) 分割为多个小事件后相加。

例题：

某车间用甲、乙、丙三台机床进行生产，各台机床次品率分别为 \(0.05\) ，\(0.04\)，\(0.02\)，它们各自的产品分别占总量的\(0.25\)，\(0.35\)，\(0.40\)，将它们的产品混在一起，求任取一个产品是次品的概率。

解：
\(P(A)=0.25*0.05+0.04*0.35+0.02*0.40=0.0345\)

贝叶斯公式

定义

与全概率公式解决的问题恰好相反，贝叶斯公式是建立在条件概率的基础上寻找事件发生的原因。

返回上图：

贝叶斯公式要求的是大事件 \(A\) 已经发生的情况下，分割中小事件 \(B_i\) 的概率。

公式

设 \(B_1,B_2,……,B_n\)是样本空间 \(\Omega\) 的一个划分， \(A\) 是任一事件，则：

\[ \begin{aligned} P(B_i|A) = \frac{P(B_i)P(A|B_i)}{\sum_{ j = 1 }^{ n }P(B_j)P(A|B_j)} \end{aligned} \]

还是这张图：

我们先看分子： \(P(B_i)P(A|B_i)\) 毫无疑问是在 \(B_i\) 范围内事件 \(A\) 的概率。

而分母 \(\sum_{ j = 1 }^{ n }P(B_j)P(A|B_j)\) 则是事件 \(A\) 发生的概率。

例题：

仍然是上面的机床awa：

某车间用甲、乙、丙三台机床进行生产，各台机床次品率分别为 \(0.05\) ，\(0.04\)，\(0.02\)，它们各自的产品分别占总量的\(0.25\)，\(0.35\)，\(0.40\)，将它们的产品混在一起，取出的零件是次品，求它是第 \(i\) 台加工的概率。

0.0345

解：
甲：\(\frac{0.25*0.05}{0.05*0.25+0.04*0.35+0.02*0.40}\) 约等于 \(0.362\)

乙和丙大家自己算吧算完了发评论区~~（骗个评论）~~检查你是否真正掌握。

杂题乱写(?)

POJ3071 Football

题目链接

翻译来源：岛田小雅

老师上课的时候课件里的博客

题目描述
\(2^n\) 个队伍参加一场单淘汰制足球锦标赛，它们被编号为 \(1,2,…,2^n\) 。每一轮比赛，未被淘汰的队伍按照升序被放在一个列表里，接下来，列表里的第 \(1\) 个队伍跟第 \(2\) 个队伍比赛，第 \(3\) 个队伍跟第 \(4\) 个队伍比赛，等等。获胜的队伍晋级下一轮，战败的队伍被淘汰。\(n\) 轮之后，只有一个队伍留下来，那个队伍就是冠军。

有一个矩阵 \(1,2,…,2^n\)，\(p_{i,j}\) 表示队伍 \(i\) 在一场比赛中战胜队伍 \(j\) 的概率，决定了哪支队伍更容易赢得冠军。

输入格式
多组测试点。每个测试点都由一个 \(n(1\leqslant{n}\leqslant{7})\) 开头，接下来的 \(2^n\) 行每行有 \(2^n\) 个值， \(i\) 行的第 \(j\) 个值是 \(p_{i,j}\) 。矩阵 \(P\) 满足对任意的 \(i\neq{j}\) , \(p_{ij}=1-p_{ji}\) ，并且对任意 \(i\)，\(p_{i_i}\)等于0.

输入结束的标志是一个数字 \(-1\)。

矩阵 \(P\) 中的所有数据都以小数给出，为避免精度问题，请使用 \(double\) 数据类型作答。

输出格式
对每个测试点输出一行整数，表示哪个队伍最有可能成为冠军。为了避免精度问题，数据保证任意两个队伍之间成为冠军的概率之差不小于 \(0.01\)。

样例
输入

2
0.0 0.1 0.2 0.3
0.9 0.0 0.4 0.5
0.8 0.6 0.0 0.6
0.7 0.5 0.4 0.0
-1

输出

样例解释：

在样例中，第一轮队伍 \(1\) 对阵队伍 \(2\) ，队伍 \(3\) 对阵队伍 \(4\) 。两场比赛的胜者在第二轮对阵来决出冠军。队伍\(2\)获得冠军的概率如下：

\[\begin{aligned} P(队伍2获胜) &=P(2击败1)P(3击败4)P(2击败3)+P(2击败1)P(4击败3)P(2击败4)\\ &=p_{21}p_{34}p_{23}+p_{21}p_{43}p_{24}\\ &=0.9\times{0.6}\times{0.4}+0.9\times{0.4}\times{0.5}\\ &=0.396 \end{aligned} \]

队伍 \(3\) 的获胜概率紧随其后，为 \(0.372\) 。

很明显的概率dp题目。

~~（但是老师不讲我肯定不会）~~

设 \(f_{i,j}\) 表示队伍 \(j\) 在第 \(i\) 轮晋级的概率。

初始化：\(f_{0,j}=1\)。

得转移方程：

\[\begin{aligned} f_{i,j}=f_{i,j}+f_{i-1,j}*f_{i-1,k}*p_{j,k} \end{aligned} \]

但是这个题的难点不在于推一个转移方程，而是如何确定队伍 \(j\) 在每一轮遇到的对手都有一个范围。

比如说我们发现，第一轮里队伍 \(1\) 与队伍 \(2\) 对决决出一个胜者，第二轮显然是 \(1\) 与 \(2\) 中胜者与 \(3\) 与 \(4\) 之间胜者决出胜者。

因此我们总结出规律：决出胜者就像合并一样，队伍 \(j\) 在第 \(i\) 轮只能与在第 \(i\) 轮和它一组且在第 \(i-1\) 轮不在一组的队伍对决，可得队伍 \(i\) 在第\(j\) 轮中遇到的队伍 \(k\)必须满足的条件：

\[\begin{aligned} (\frac{j}{2^{i-1}}\neq{\frac{k}{2^{i-1}}}\bigwedge{\frac{j}{2^i}={\frac{k}{2^i}}}) \end{aligned} \]

（ps:\(\bigwedge\)的意思是并列）

于是有代码：

Miku's Code

#include<iostream>
#include<stdio.h>
//因为是poj的题所以没有万能头 
using namespace std;

const int maxn = (1<<8)+2;
int n,nlen;
double p[maxn][maxn],f[maxn][maxn];

void input(){
	nlen=(1<<n);
    for(int i=0;i<nlen;++i){
        for(int j=0;j<nlen;++j){
           	scanf("%lf",&p[i][j]);	
		}
        f[0][i]=(double)1.0;
    }	
}

void work(){
	for(int i=1;i<=n;++i){
        for(int j=0;j<nlen;++j){
            f[i][j]=(double)0.0;
            //不要忘记 
            for(int k=0;k<nlen;++k){
				if(j==k)	continue; 
                if(j/(1<<(i-1))!=k/(1<<(i-1)) && j/(1<<i)==k/(1<<i))
					f[i][j]+=f[i-1][j]*f[i-1][k]*p[j][k];
            }
        }
	}
}

int main(){
    while(scanf("%d",&n) && n!=-1){
        input();
        work();
        int ans=0;
        for(int i=1;i<nlen;i++){	//遍历每一个队伍 
			if(f[n][ans]<f[n][i]) ans=i;
		}
        printf("%d\n",ans+1);		//我们的队伍编号是从0开始的 
    }
    return 0;
}