动态规划（2）

闲时记录 / 2023-05-07 / 原文

线性DP
数字三角形

给定一个如下图所示的数字三角形，从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点，一直走到底层，要求找出一条路径，使路径上的数字的和最大。

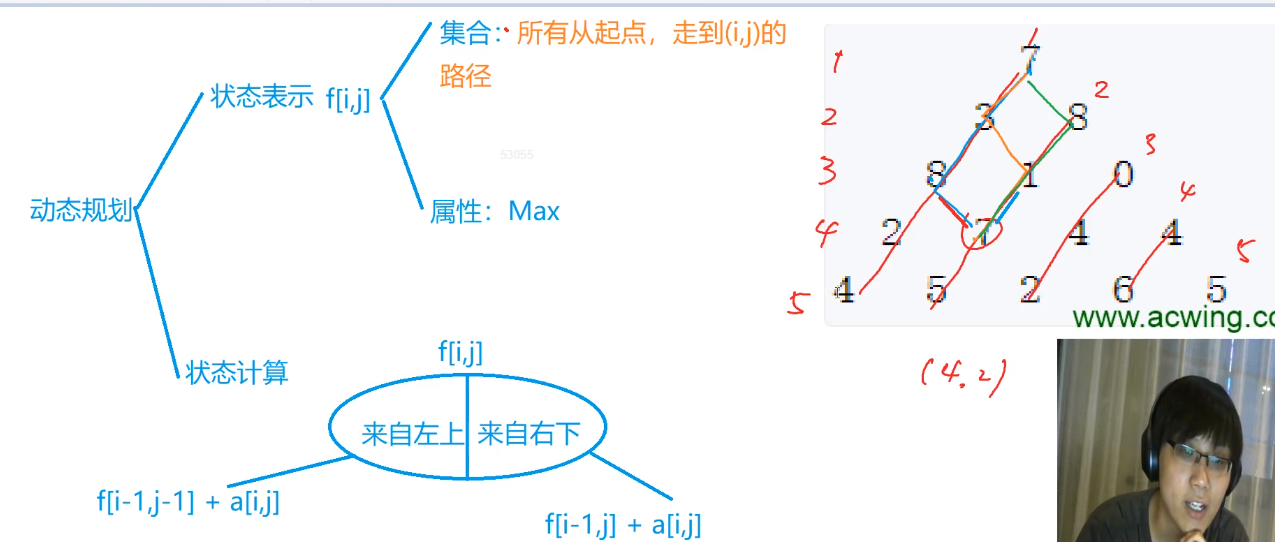
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 3e3+10, INF = 1e9  ; 
int n ; 
int a[N][N] ; 
int f[N][N] ; 
 
int main(){
     
    cin>> n ; 
    
    for(int i=1 ; i<=n; i++ )
        for(int j=1 ; j<=i ; j++)
            cin>>a[i][j] ; 

     for(int i=1; i<=n ; i++)
         for(int j=0; j<=i+1 ; j++)    // 初始化时，要多初始化最左边点的左上角和最右边点的右上角 
            f[i][j] = -INF ;     //负的无穷大 
     
    f[1][1] = a[1][1] ; 
    
    for(int i=2 ; i<=n ;i++ )
        for(int j=1 ; j<=i ; j++)
            f[i][j] = max(f[i-1][j-1]+a[i][j], f[i-1][j] + a[i][j]) ; 
            // 来自左上和右上的最大路加上当前点
    int res = -INF ;     
    for(int i=1; i<=n ; i++ ) 
        res = max(res, f[n][i] ) ; // 遍历底部节点，选出最大的 
                             
    cout<<res<<endl ;     
    return 0;
}

最长上升子序列

给定一个长度为

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 3e3+10 ; 
int n ; 
int a[N]; 
int f[N] ; 
 
int main(){        
    cin>>n ; 
    for(int i=1; i<=n; i++) cin>>a[i] ; 
    
    for(int i=1; i<=n; i++)
    {
        f[i] = 1; // 只有a[i]一个数 
        for(int j=1; j<i; j++ )
            if(a[j]<a[i])
                f[i] = max(f[i], f[j]+1) ; 
    }
    
    int res = 0 ;
    for(int i=1; i<=n; i++) // 找最大的
        res = max(res, f[i]) ;
             
    cout<<res<<endl ;     
    return 0;
}

最长公共子序列

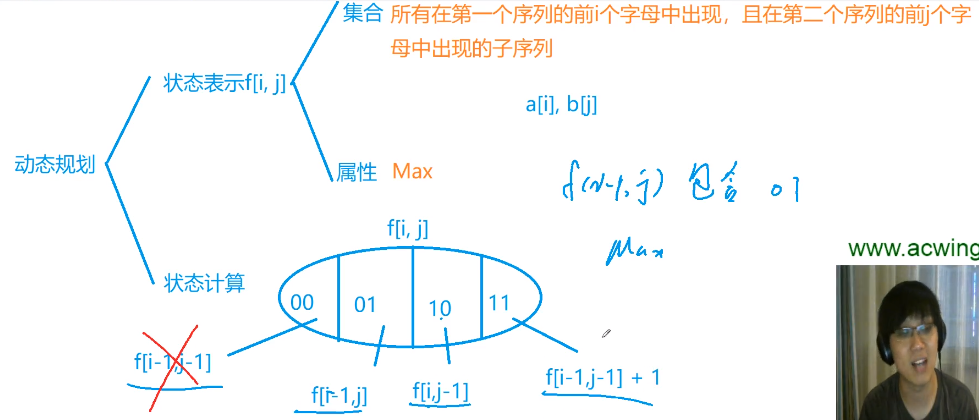
#include <iostream>
#include <algorithm>
using namespace std ;
const int N = 1010 ; 
int n,m ; 
char a[N], b[N]; 
int f[N][N] ;

int main(){
    
    cin>>n>>m ; 
    scanf("%s%s", a+1, b+1 ) ; 
    
    for(int i=1; i<=n ;i++)
    {
        for(int j=1 ; j<=m ; j++)
        {
            f[i][j] = max(f[i-1][j], f[i][j-1]) ; 
            if(a[i]==b[j]) f[i][j] = max(f[i][j], f[i-1][j-1]+1) ; 
        }
    }
    cout<<f[n][m] ; 
    return 0 ;
}

最短编辑距离

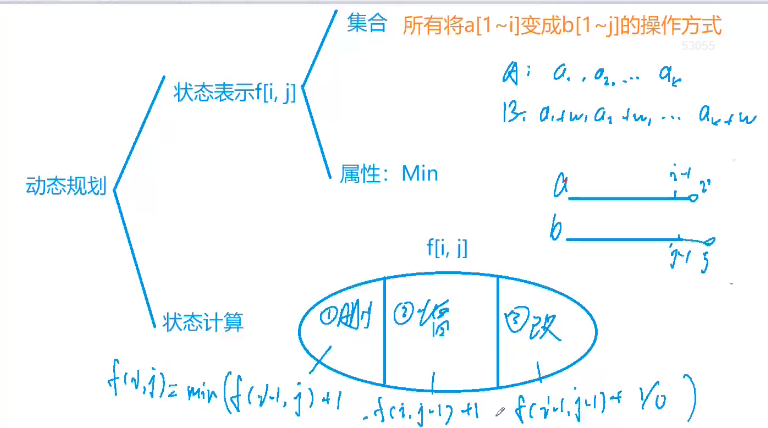
#include <iostream>
#include <algorithm>
using namespace std ;

const int N = 1010 ; 

int n,m ; 
char a[N], b[N]; 
int f[N][N] ;

int main(){
    
    scanf("%d%s%d%s",&n, a+1,&m, b+1 ) ; 
    for(int i=0; i<=m ; i++) f[0][i] = i; //a为空，肯定是添加
    for(int j=0; j<=n ; j++) f[j][0] = j ;//b为空，肯定是删除
    
    for(int i=1; i<=n ;i++)
    {
        for(int j=1 ; j<=m ; j++)
        {
            f[i][j] = min(f[i-1][j]+1, f[i][j-1]+1) ; 
            if(a[i]==b[j]) f[i][j] = min(f[i][j], f[i-1][j-1]) ;
            else f[i][j] = min(f[i][j], f[i-1][j-1]+1) ; 
        }
    }
    cout<<f[n][m] ; 
    return 0 ;
}

区间DP

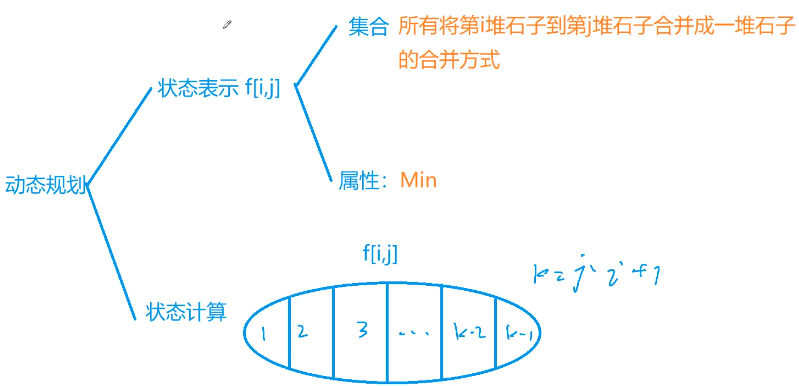
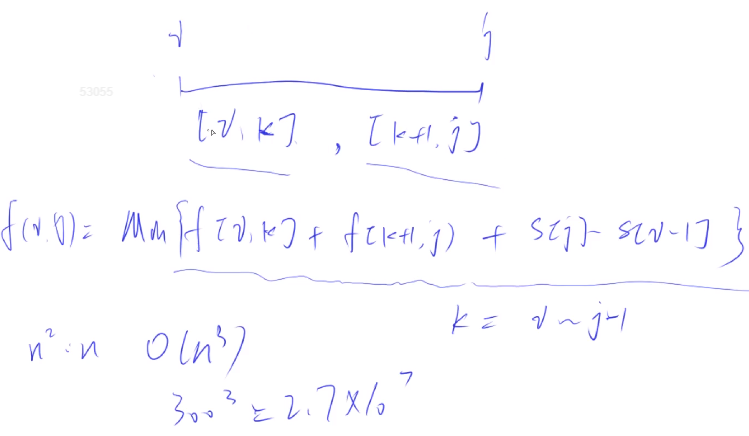
#include <iostream>
#include <algorithm>
using namespace std ;

const int N = 1010 ; 

int n; 
int s[N] ; // 前缀和
int f[N][N] ;

int main(){
    
    cin>>n;  
    
    for(int i=1; i<=n; i++) cin>>s[i] ;
    
    for(int i=1; i<=n; i++) s[i] += s[i-1] ;
    
    for(int len = 2; len<=n; len++)
    {
        for(int i=1; i+len-1 <= n; i++)
        {
            int l=i, r = i+len-1 ; 
            f[l][r] = 8e7 ; // 先初始化为一个较大
            for(int k=l ; k<r; k++)
                f[l][r] = min( f[l][r], f[l][k] + f[k+1][r] + s[r] - s[l-1]) ;
        }
    }

    cout<<f[1][n] ;  // 从第1堆到第n堆合并的最小代价
    
    return 0 ;
}