AC 自动机学习笔记

masterhuang's blog / 2023-05-07 / 原文

前置知识：\(\texttt{trie}\) 树。不会的话到这篇博客看看吧。

前置知识：\(\texttt{kmp}\)。不会的话到这篇博客看看吧。

字符串好的题单。下面设所有字符串的大小之和为 \(|\Sigma|\)。

\(\texttt{AC}\) 自动机（也叫 \(\texttt{ACAM}\)）

定义与构建

\(\texttt{ACAM}\) 时为了解决 \(\lceil\) 多个字符串在一个字符串上的匹配 \(\rfloor\) 的问题。设多个字符串为 \(S_1,S_2,\dots,S_n\)，那一个字符串为 \(T\)。

如果暴力 \(\texttt{kmp}\) 的话复杂度为 \(|\Sigma||T|\)，显然会爆炸。

我们把 \(S_1,S_2,\dots,S_n\) 建成一颗 \(\texttt{trie}\) 树。

比如这样，灰色是结尾。

接下来是最重要的一步：构建 \(\texttt{fail}\) 指针。

这一步与 \(\texttt{kmp}\) 算法中的 \(\texttt{next}\) 数组是类似的，通过跳转来省略重复的检查。

那么要如何构建呢？我先把构建好的放出来。

每次沿着 \(\texttt{trie}\) 树匹配，匹配到当前位置没有匹配上时，直接跳转到 \(\texttt{fail}\) 指针所指向的位置继续进行匹配。

下面考虑如何求 \(\texttt{fail}\) 指针。

沿着其父节点的失配指针一直向上，直到找到拥有当前这个字母的子节点的节点的那个子节点，如果没有就指向 \(\texttt{trie}\) 树的根。但是直接按这个定义做的话复杂度还是会爆炸。

具体实现的时候我们把 \(\texttt{fail}\) 数组当做一个辅助数组。把 \(\texttt{trie}\) 树中的儿子数组（每个点的 \(\texttt{next}\) 数组）充分利用起来。

构建过程：考虑字典树中当前的结点 \(u\)，\(u\) 的父结点是 \(p\)，\(p\) 通过字符 \(c\) 的边指向 \(u\)，即 \(\text{trie}[p,\mathtt{c}]=u\)。假设深度小于 \(u\) 的所有结点的 \(fail\) 指针都已求得。

如果 \(\text{trie}[\text{fail}[p],\mathtt{c}]\) 存在：则让 \(u\) 的 \(fail\) 指针指向 \(\text{trie}[\text{fail}[p],\mathtt{c}]\)。相当于在 \(p\) 和 \(\text{fail}[p]\) 后面加一个字符 \(c\)，分别对应 \(u\) 和 \(fail[u]\)。
如果 \(\text{trie}[\text{fail}[p],\mathtt{c}]\) 不存在：那么我们继续找到 \(\text{trie}[\text{fail}[\text{fail}[p]],\mathtt{c}]\)。重复 \(1\) 的判断过程，一直跳 \(fail\) 指针直到根结点。
如果真的没有，就让 \(fail\) 指针指向根结点。
如此即完成了 \(\text{fail}[u]\) 的构建。相信大家自己结合代码都能理解构建和匹配的过程。构建复杂度 \(O(|\Sigma|)\)。匹配复杂度 \(O(|\Sigma|+|T|)\)。都是线性的。

这种构建方式很妙，大家可以参考这个动图理解。

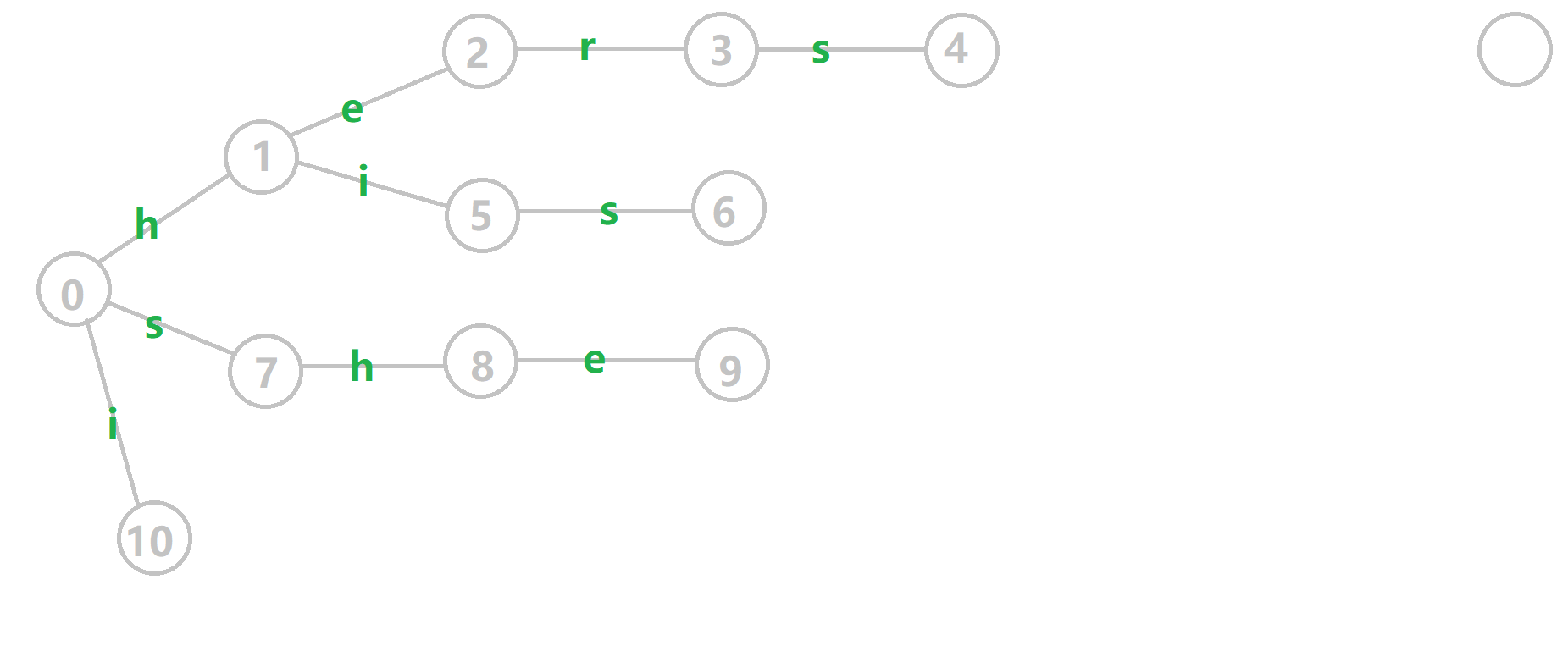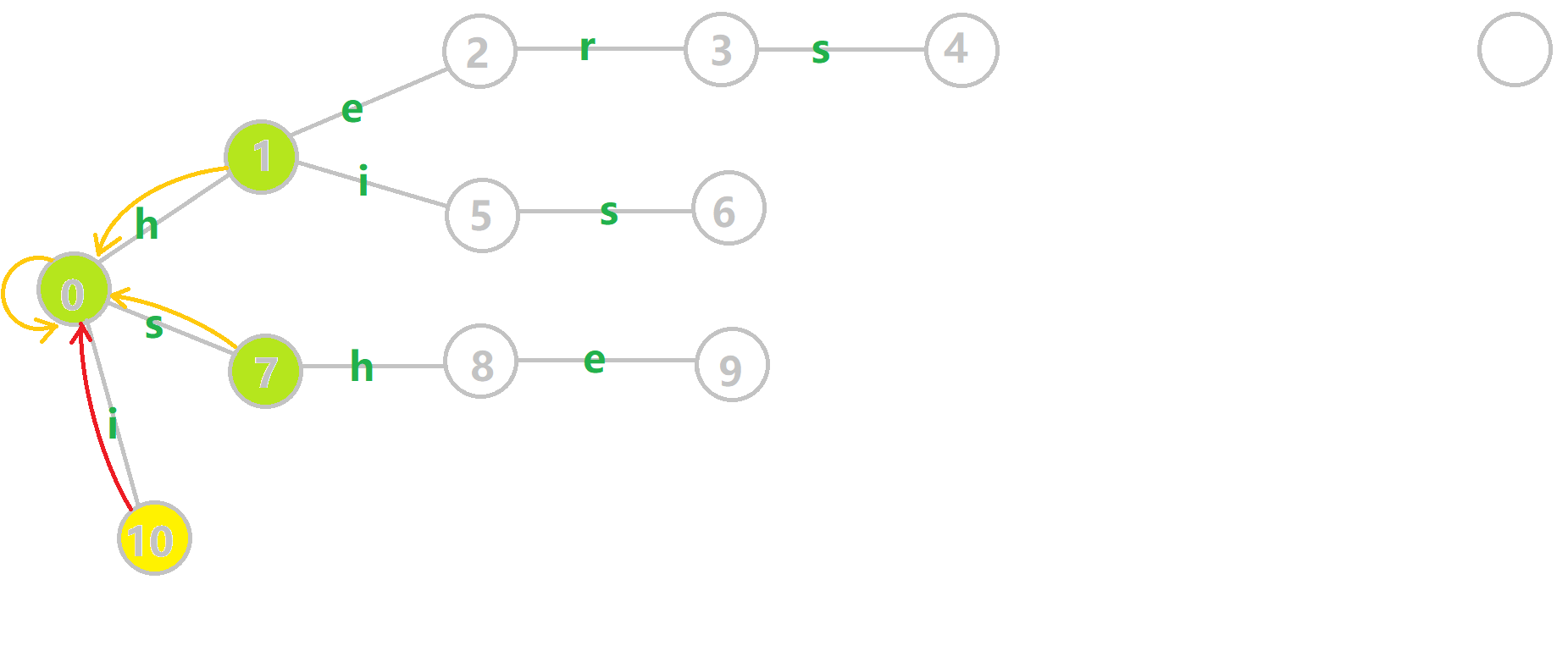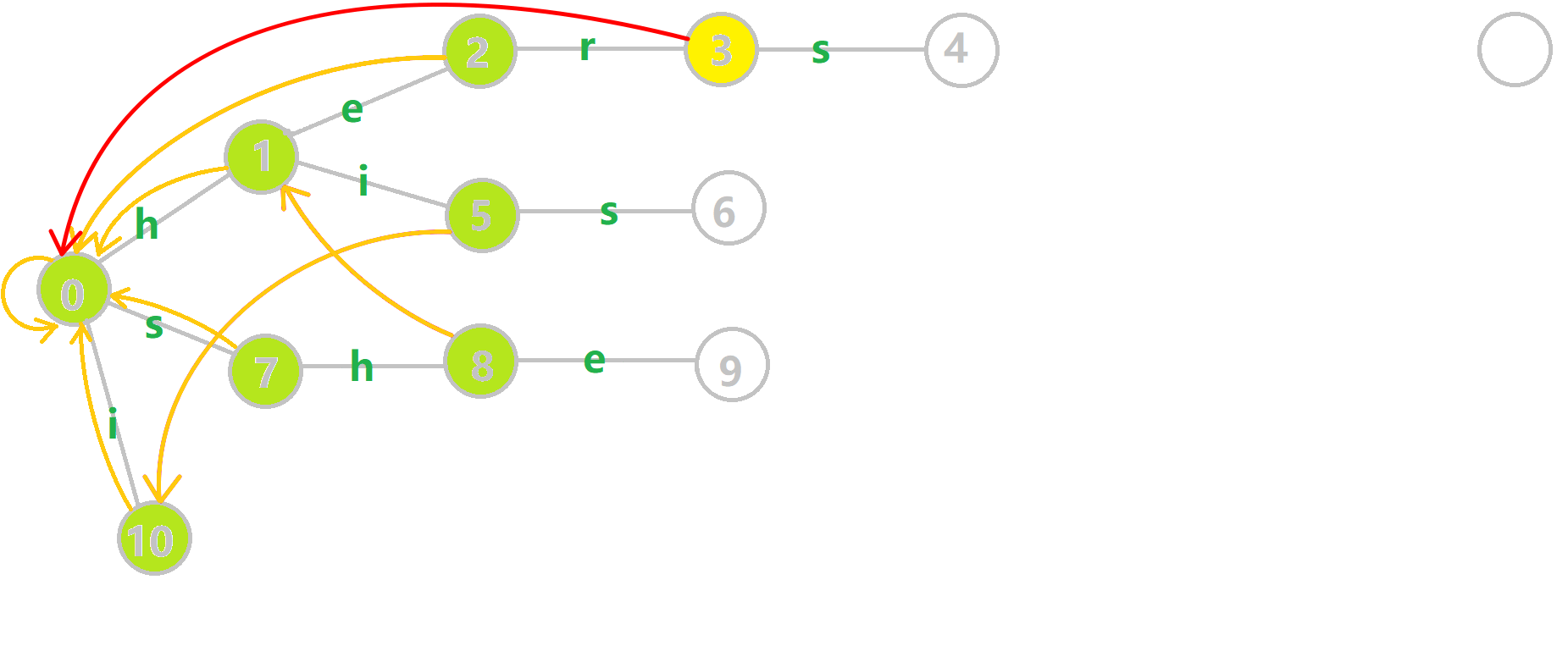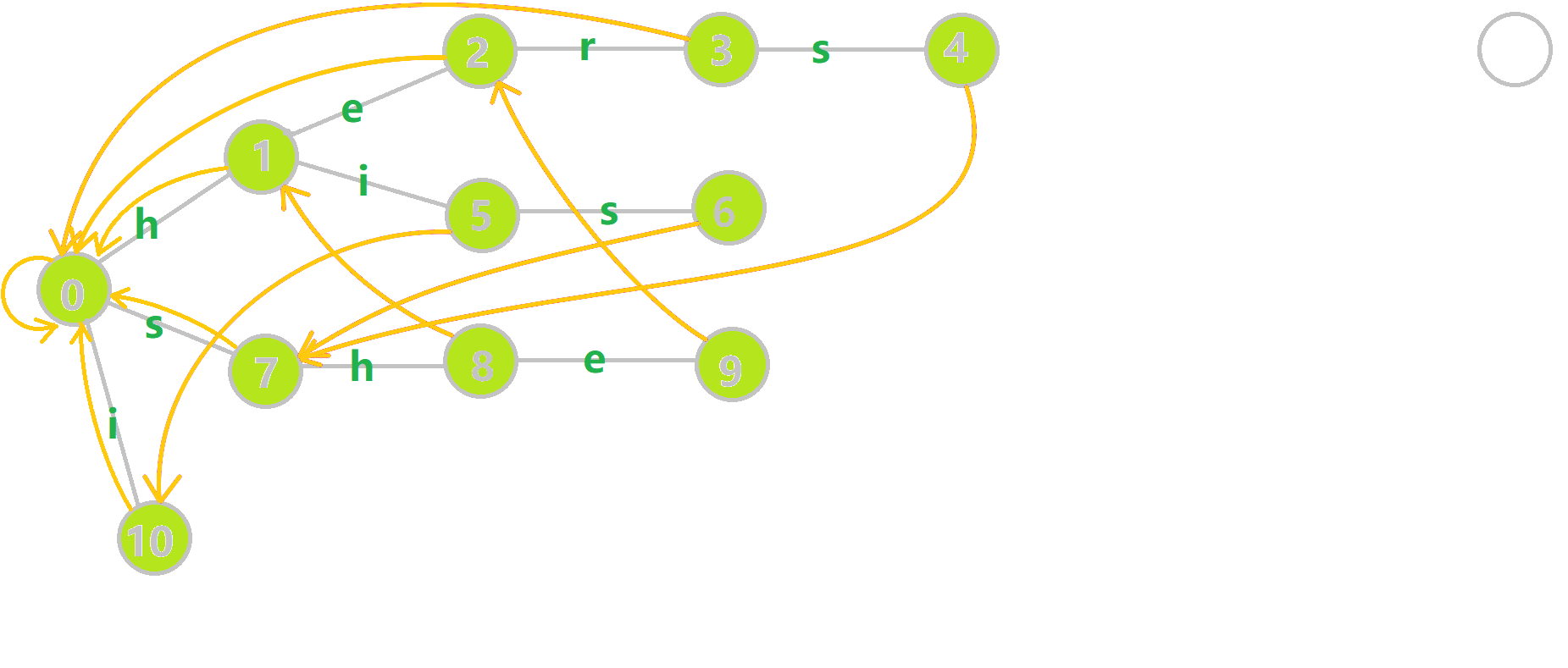
代码（\(\texttt{by yyb}\)）

void Get_fail()//构造fail指针
{
	    queue<int> Q;//队列 
	    for(int i=0;i<26;++i)//第二层的fail指针提前处理一下
        	   if(AC[0].vis[i]!=0)
        	   {
        	       AC[AC[0].vis[i]].fail=0;//指向根节点
        	       Q.push(AC[0].vis[i]);//压入队列 
        	   }
	    while(!Q.empty())//BFS求fail指针 
	    {
	    	  int u=Q.front();
	    	  Q.pop();
			  for(int i=0;i<26;++i)//枚举所有子节点
			  {
			  	      if(AC[u].vis[i]!=0)//存在这个子节点
					  {
					  	           AC[AC[u].vis[i]].fail=AC[AC[u].fail].vis[i];
//子节点的fail指针指向当前节点的fail指针所指向的节点的相同子节点 
					  	      Q.push(AC[u].vis[i]);//压入队列 
					  }
					  else//不存在这个子节点 
					  AC[u].vis[i]=AC[AC[u].fail].vis[i];
					  //当前节点的这个子节点指向当前节点fail指针的这个子节点 
		      }
	    }
}
int AC_Query(string s)//AC自动机匹配
{
        int l=s.length();
        int now=0,ans=0;
        for(int i=0;i<l;++i)
        {
                now=AC[now].vis[s[i]-'a'];//向下一层
                for(int t=now;t&&AC[t].end!=-1;t=AC[t].fail)//循环求解
                {
                         ans+=AC[t].end;
                         AC[t].end=-1;
                } 
        }
        return ans;
}

上面是 P3808 模板1 的主要代码。

一个性质

注意到 \(\texttt{fail}\) 指针最终构成了一颗树，于是跳 \(\texttt{fail}\) 指针的过程可以转化为树上操作。

比如 \(P3796,P5357\)，是两个加强版。以二次加强版为例：

我们要不断跳 \(\texttt{fail}\) 指针，对跳到的节点权值 \(+1\)，最后 \(O(n)\) 次查询某个点的权值。

转化为树上操作后显然是个树上差分问题，建出 \(\texttt{fail}\) 树然后树上差分做即可。保证了复杂度为 \(O(|\Sigma|+|T|)\)。

struct trie{int nex[26],fail,x;}a[N];
int n,tot,b[N];string c[N],x;
vector<int>g[N];
inline void Push(int I,string x)
{
	int wz=0;
	for(int i=0;i<x.size();i++)
	{
		int to=x[i]-'a';
		if(!a[wz].nex[to]) a[wz].nex[to]=++tot;wz=a[wz].nex[to];
	}b[I]=wz;
}
inline void ACAM()
{
	queue<int>q;for(int i=0;i<26;i++) if(a[0].nex[i]) q.push(a[0].nex[i]),g[0].push_back(a[0].nex[i]);
	while(!q.empty())
	{
		int t=q.front();q.pop();
		for(int i=0;i<26;i++)
		{
			int u=a[t].nex[i],v=a[a[t].fail].nex[i];
			u?q.push(u),g[v].push_back(u),a[u].fail=v:a[t].nex[i]=v;
		}
	}
}
void dfs(int x,int fa){for(int i:g[x]) if(i!=fa) dfs(i,x),a[x].x+=a[i].x;}
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	cin>>n;for(int i=1;i<=n;i++) cin>>c[i],Push(i,c[i]);
	ACAM();cin>>x;int wz=0,mx=0;
	for(int i=0;i<x.size();i++) a[wz=a[wz].nex[x[i]-'a']].x++;dfs(0,-1);
	for(int i=1;i<=n;i++) cout<<a[b[i]].x<<"\n";
	return 0;
}