质数和约数

SunnyYuan的博客 / 2023-07-14 / 原文

试除法

思想：

要检验一个数字 \(n\) 是否为质数，将 \(n\) 除以 \(1\sim \sqrt n\)，如果有一个数字刚好整除 \(n\)，那么 \(n\) 为合数，否则 \(n\) 为奇数。

代码：

bool prime(int x) {
    if (x < 2) return false;
	for (int i = 2; i <= x / i; i++) {
		if (x % i == 0) {
			return false;
		}
	}
	return true;
}

埃氏筛

思想：

埃氏筛直接利用质数的定义。

我们易知一个数 \(x\) 的 \(n\) 倍一定是一个合数，

那么我们遇到一个质数时 \(x\)，我们可以把它的倍数 \(x \times n\) 全部标记为不是质数。

例：

遇到质数 \(2\)（绿色）：

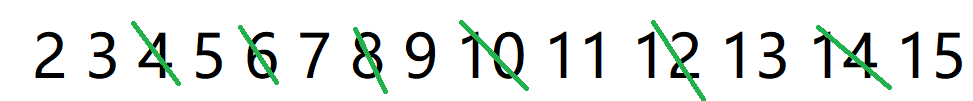
遇到质数 \(3\)（红色）：

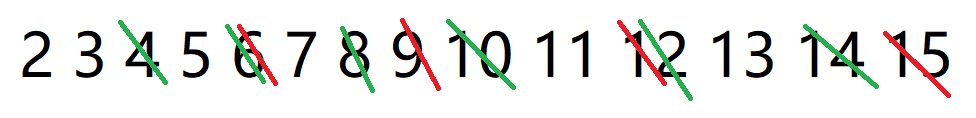
遇到质数 \(5\)（橙色）：

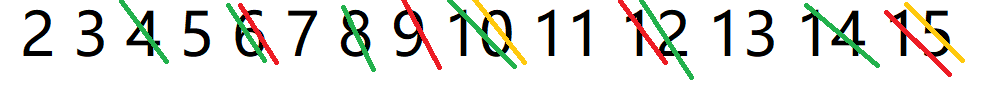
遇到质数 \(7\)（蓝色）：

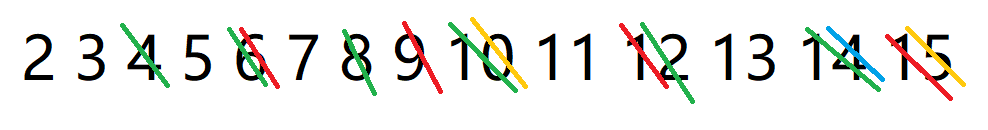
等等。

我们还有一些优化：

我们遇到质数 \(x\)，可以直接从 \(x \times x\) 开始划，因为前面的 \(x \times i\) 已经被更小的质数筛掉了，比如 \(20\) 通过 \(5 \times 4\) 筛掉，但早已经通过 \(2 \times 10\) 筛掉了。
我们可以只枚举 \(1 \sim \sqrt n\)，道理与试除法相同。

代码：

#include <bits/stdc++.h>

using namespace std;

const int N = 1000010;

int n;
int prime[N], cnt;
bool is_not_prime[N];

void get_prime() {
    is_not_prime[0] = is_not_prime[1] = true;
    for (int i = 2; i <= n / i; i++) {
        if (!is_not_prime[i]) {
            for (int j = i * i; j <= n; j += i) {
                is_not_prime[j] = true;
            }
        }
    }
    for (int i = 2; i <= n; i++) {
        if (!is_not_prime[i]) {
            prime[++cnt] = i;
        }
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    cin >> n;
    get_prime();
    cout << cnt << '\n';
    
    return 0;
}