并查集(Disjoint Set)
并查集是算法竞赛中常用的一种数据结构。
其主要功能是查询两个元素是否在同一个集合以及将两个集合合并。
第一部分 并查集的基本操作
算法思想
- 我们将所有元素建成很多树(森林),每一棵树就是一个集合,比如下图有 \(\{1, 2, 3, 4, 5, 6\}, \{7, 9, 10, 11, 12, 13\}\) 两个集合。
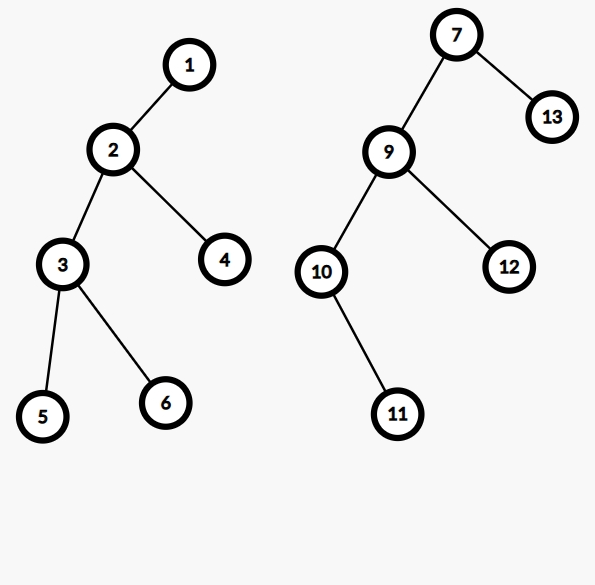
- 我们将每一棵树的根当作判断依据,当我们要查询两个元素是否在同一个集合时,可以判断它们是否在同一棵树上,即只要判断它们所在树的根相同与否就可以了,比如下图 \(2, 3\) 有相同的根 \(1\),它们便在一个集合,但是 \(2, 9\) 分别拥有根 \(1, 7\),不在同一个集合。
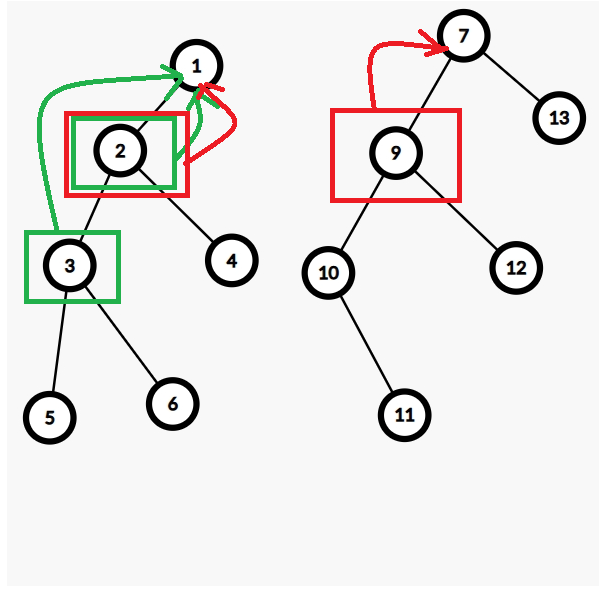
- 当我们要合并两个集合时,只要两棵树合并即可,即只要把两棵树的根节点连接起来就可以了。
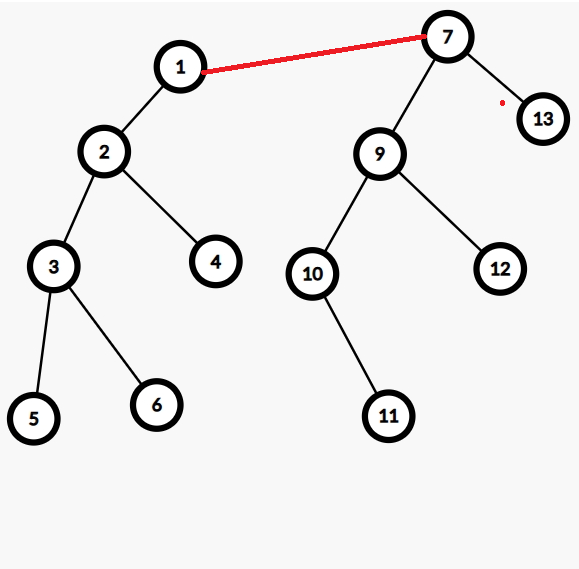
- 最开始时,每个元素各为一棵树并且自己就是根。

算法优化
我们发现,如果建出来的树长这样:
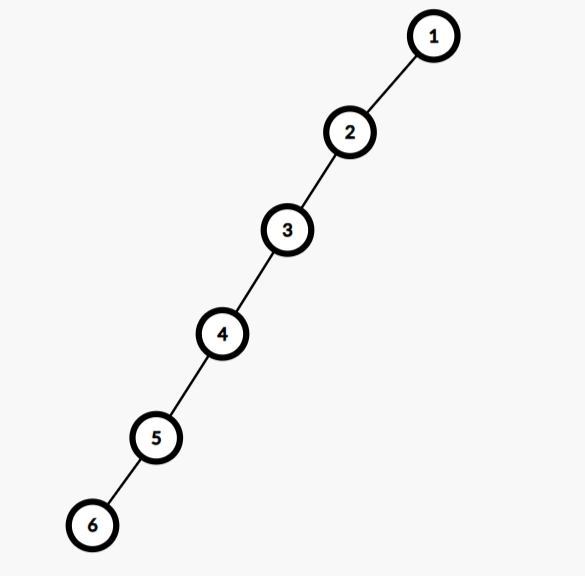
多次查找非常费时间,因为每次都要从最下面跑到最上面。
因为它们都是一个集合的,不在乎它在集合中的顺序,所以我们可以把树变成这样:
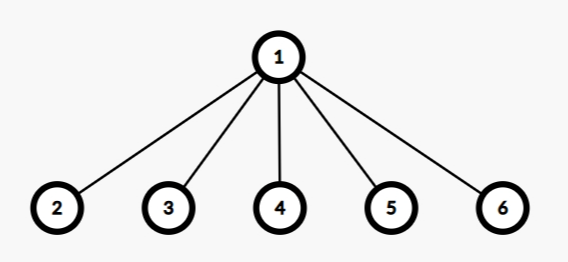
即每次查询一个元素在哪一个集合的时候直接把它接在根节点上。
这个可以通过递归实现。
例题1:HDU 1213 How many tables
题目描述

思路
认识的人合并为一个集合,最后查找有多少个集合即可。
查询集合数量有两种方法:
方法1:等所有操作进行完成以后,我们可以查询有多少棵树,也就是查找有多少个根;
方法2:我们定义 \(cnt\) 初始值为 \(n\),当合并两个不同的集合时,\(cnt\) 就可以 \(-1\),代表两个集合合并,集合数量少了一个。
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
int fa[N];
void init() {
for (int i = 1; i <= n; i++) fa[i] = i;
}
int find(int u) {
if (u == fa[u]) return u;
return fa[u] = find(fa[u]);
}
void merge(int a, int b) {
int fx = find(a), fy = find(b);
if (fx != fy) fa[fx] = fy;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) {
cin >> n >> m;
int cnt = n;
init();
for (int i = 1; i <= m; i++) {
int x, y;
cin >> x >> y;
if (find(x) != find(y)) cnt--;
merge(x, y);
}
cout << cnt << '\n';
}
return 0;
}