二叉树的操作
二叉树的操作
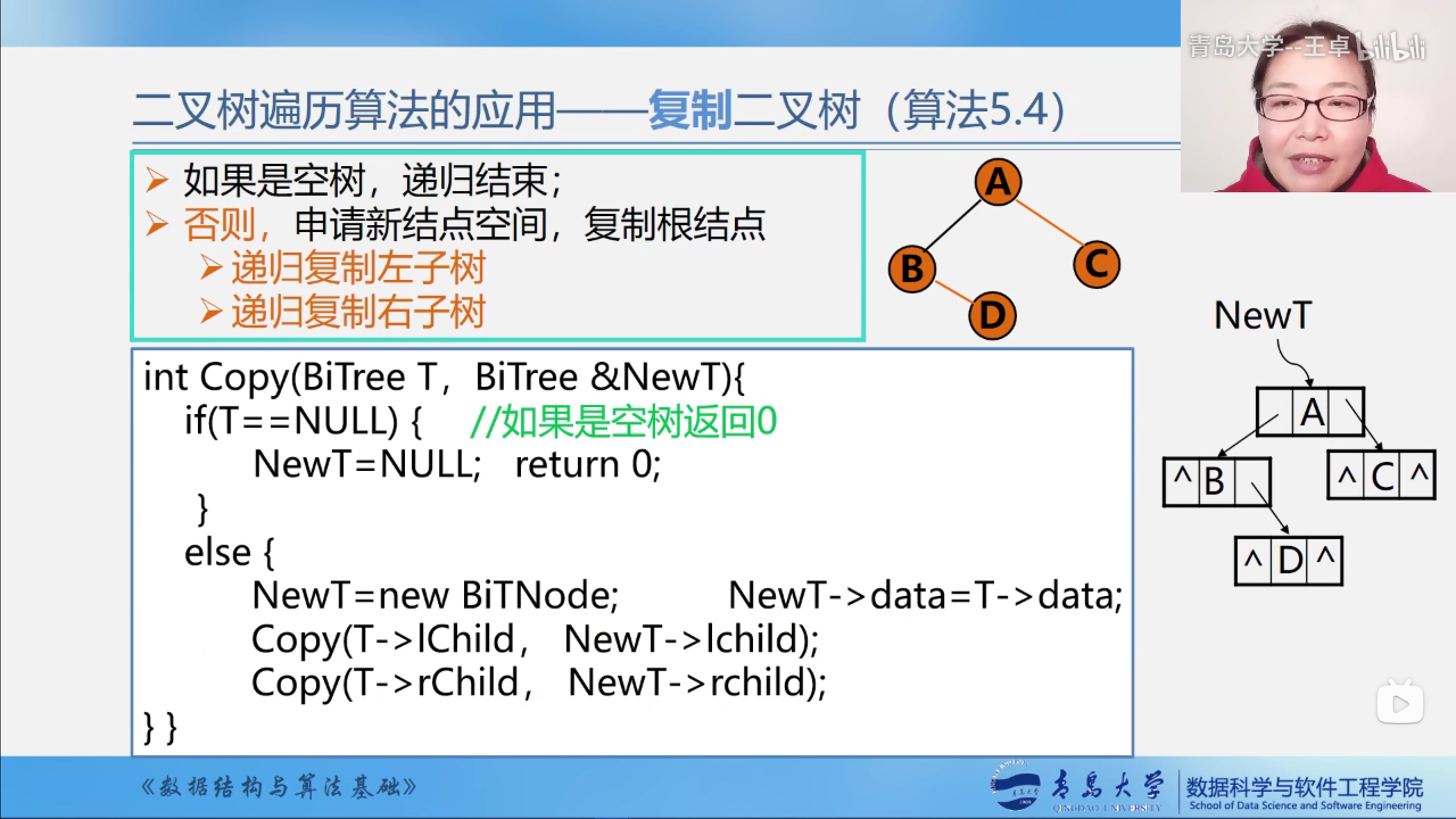
二叉树的复制
如果是空树,递归结束
否则, 申请新结点的空间,复制根结点
- 递归复制左子树
- 递归复制右子树
代码实现
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>
#include <cstring>
#include <unordered_set>
#include <set>
#include <stack>
#include <map>
#include <cmath>
#include <sstream>
#include <queue>
using namespace std;
typedef struct BiNode {
char data;
struct BiNode* lchild, *rchild;
} BiNode, *BiTree;
void CreateBitree(BiTree &T) {
char ch;
cin >> ch;
if (ch != ',') {
T = new BiNode; //创建一个新结点
T->data = ch;
CreateBitree(T->lchild);
CreateBitree(T->rchild);
} else {
T = NULL;
return;
}
}
/*
二叉树复制函数
需要两个二叉树的根结点
*/
void copyBiTree(BiTree T, BiTree &NewT) {
if (T == NULL) { //如果旧树的地址只为空
NewT = NULL; //那么新树的地址值也为空
} else {
NewT = new BiNode; //创建一个新结点
NewT->data = T->data; //将旧树的值域赋值给新树
copyBiTree(T->lchild, NewT->lchild); //递归复制左子树
copyBiTree(T->rchild, NewT->rchild); //递归复制右子树
}
}
void DLR(BiTree T) {
if (T != NULL) {
cout << T->data;
DLR(T->lchild);
DLR(T->rchild);
} else {
return;
}
}
int main () {
BiTree root = NULL;
CreateBitree(root);
DLR(root);
cout << '\n';
BiTree Newroot = NULL;
copyBiTree(root, Newroot);
DLR(Newroot);
return 0;
}
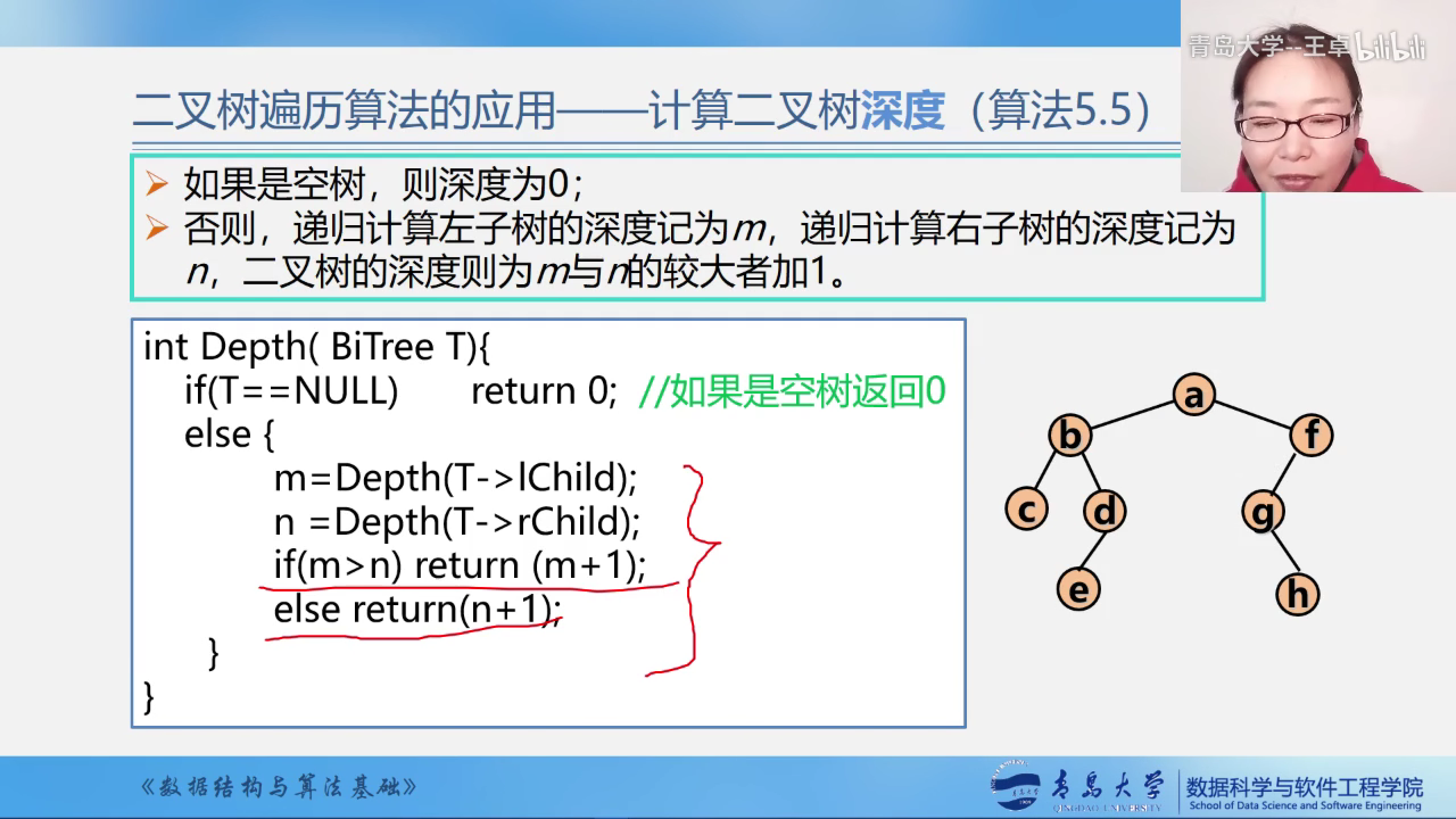
计算二叉树的深度
如果是空树,则深度为0;
否则,递归计算左子树的深度记为m,递归计算右子树的深度记为n,二叉树的深度则为m与n的较大者加1
代码示例
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>
#include <cstring>
#include <unordered_set>
#include <set>
#include <stack>
#include <map>
#include <cmath>
#include <sstream>
#include <queue>
using namespace std;
typedef struct BiNode {
char data;
struct BiNode* lchild, *rchild;
} BiNode, *BiTree;
void CreateBitree(BiTree &T) {
char ch;
cin >> ch;
if (ch != ',') {
T = new BiNode; //创建一个新结点
T->data = ch;
CreateBitree(T->lchild);
CreateBitree(T->rchild);
} else {
T = NULL;
return;
}
}
/*
二叉树深度计算函数
返回值为二叉树的深度
*/
int Depth(BiTree T) {
int m = 0, n = 0; //m用来记录左子树的深度,n用来记录右子树的深度
if (T == NULL) {
return 0;//空树的返回值为0
} else {
m = Depth(T->lchild);//递归计算左子树
n = Depth(T->rchild);//递归计算右子树
if (m > n) {
return m + 1;//取m,n的较大值加1
//然后返回
} else {
return n + 1;
}
}
}
void DLR(BiTree T) {
if (T != NULL) {
cout << T->data;
DLR(T->lchild);
DLR(T->rchild);
} else {
return;
}
}
int main () {
BiTree root = NULL;
CreateBitree(root);
DLR(root);
cout << '\n';
cout << Depth(root) << '\n';
return 0;
}
题目链接
104. 二叉树的最大深度
AC代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
int m=0,n=0;
if(root==NULL)
{
return 0;
}
else
{
m=maxDepth(root->left);
n=maxDepth(root->right);
if(m>n)
{
return m+1;
}
else
{
return n+1;
}
}
}
};
计算二叉树的结点总数
如果是空树,则结点的个数为0;
否则,结点个数为:左子树的结点个数+右子树的结点个数再+1

代码实现
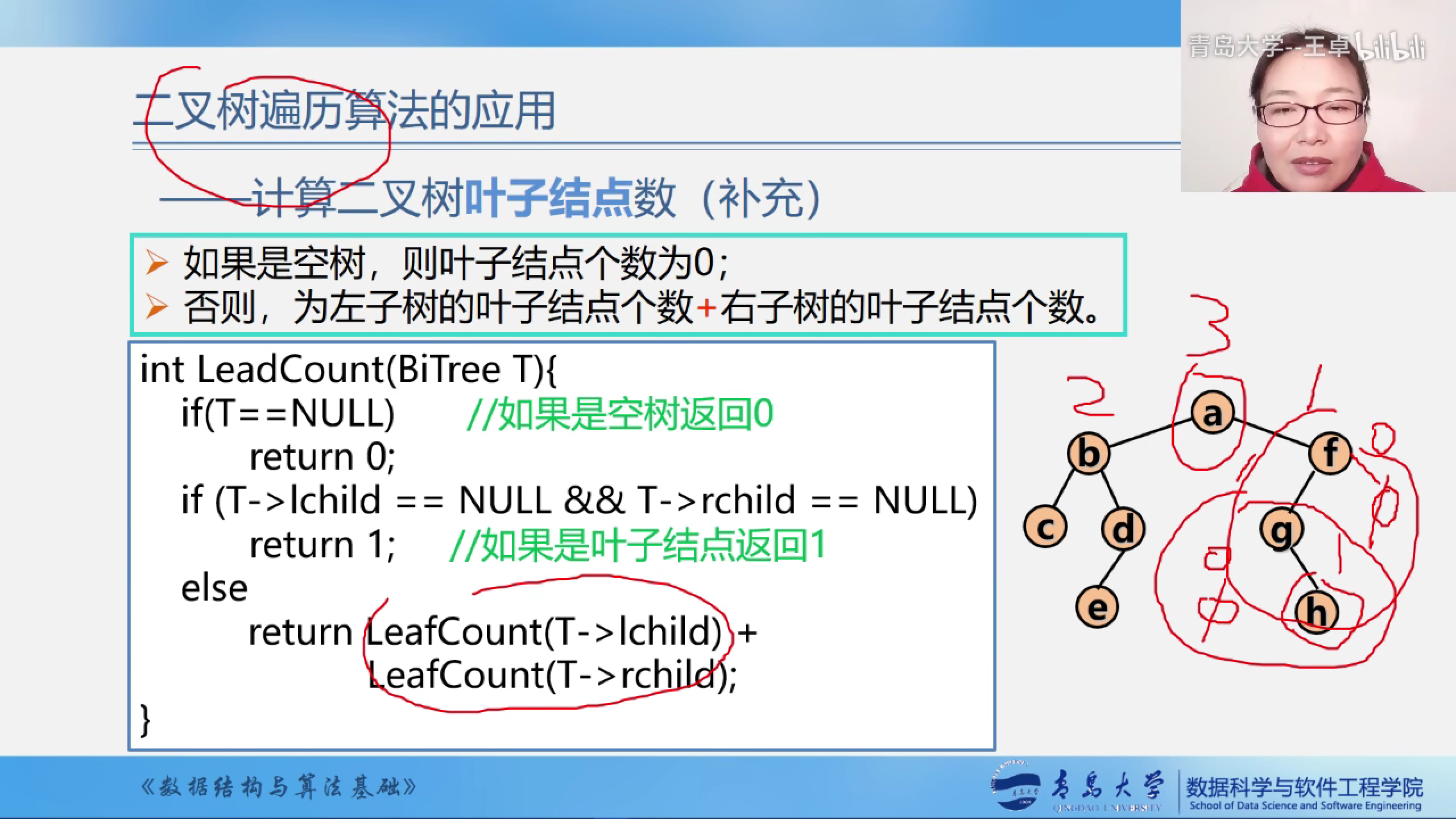
计算二叉树的叶子结点数
如果是空树,则叶子结点个数为0;
否则,为左子树的叶子结点个数+右子树的叶子结点个数.