前言

终于把线性动态规划学完了，本蒟蒻要开始背包了，祝我好运吧！如果文章有任何问题，欢迎评论或者私信让我知道🌹。

[NOIP2001 普及组] 装箱问题

题目描述

有一个箱子容量为 \(V\)，同时有 \(n\) 个物品，每个物品有一个体积。

现在从 \(n\) 个物品中，任取若干个装入箱内（也可以不取），使箱子的剩余空间最小。输出这个最小值。

输入格式

第一行共一个整数 \(V\)，表示箱子容量。

第二行共一个整数 \(n\)，表示物品总数。

接下来 \(n\) 行，每行有一个正整数，表示第 \(i\) 个物品的体积。

输出格式

• 共一行一个整数，表示箱子最小剩余空间。

样例 #1

样例输入 #1

24
6
8
3
12
7
9
7

样例输出 #1

0

我的代码

#include<iostream>
#define int long long
const int N = 2e5 + 5;
bool dp[N];
signed main(){
    int v,n;
    std::cin>>v>>n;
    int ans[n + 1];
    for(int i  =1;i <= n;i ++) {
        std::cin >> ans[i];
    }
    dp[0] = true;
    for(int i = 1;i <=n ;i ++){
        for(int j = v;j >= ans[i];j --){
            dp[j] = dp[j] || dp[j - ans[i]];
        }
    }
    for(int i = v;i >= 0;i --){
        if(dp[i]){
            std::cout<<v - i<<"\n";
            return 0;
        }
    }
    return 0;
}

解题思路

1、先考虑二维数组dp[i][j]，表示在继承前面所有状态的情况下，第i个物品是否放进背包的两种状态下，背包所用的体积j

2、因为每个物品都可以选择放或者不放（注意放入背包的条件是剩余的空间充足），所有dp[i][j]可以继承dp[i-1][j]或者dp[i - 1][j - v[i]]的状态

3、不难发现，dp[i - 1][j]为true的话，dp[i][j]必定为true，dp[i][j]是在dp[i - 1][j]的基础上进行叠加。所以可以优化为一维数组dp[i]，表示背包中使用了i体积的状态

4、一维数组的状态转移方程可以优化为dp[j] = dp[j] || dp[j - v[i]]，需要注意的是，前面的状态会对后面的状态造成影响，所以，我们从后向前遍历。又因为继承了前面的状态，所以当j - v[i] < 0时的状态不需要进行修改。

01背包

题目描述

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。第 i 件物品的体积是 vi，价值是 wi。求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。
接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

样例

输入样例

4 5
1 2
2 4
3 4
4 5

输出样例：

8

我的代码

#include<iostream>
#include<math.h>
#define int long long
const int N = 1e3 + 5;
int dp[N];
signed main(){
    int V,n,ans = 0;
    std::cin >> n >> V;
    int v[n + 1],w[n + 1];
    for(int i = 1;i <= n;i ++) {
        std::cin >> v[i] >> w[i];
    }
    for(int i = 1;i <=n ;i ++){
        for(int j = V; j >= v[i]; j --){
            dp[j] = std::max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    std::cout<<dp[V]<<"\n";
    return 0;
}

解题思路

基本和上面一样，只不过数组内存的值变成了当前价值。

完全背包

题目描述

有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。

第 i 种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 种物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤1000
0<vi,wi≤1000

样例

输入样例

4 5
1 2
2 4
3 4
4 5

输出样例：

10

解题思路

完全背包其实就是01背包的bug版，还记得01背包的内层循环是从哪开始的吗？从后开始遍历是为了规避前面放入物品的操作对后面的影响，因为01背包的物品只能放入一次，是不是感觉晕乎乎的，不知道我在说啥？那就画个表来理解一下

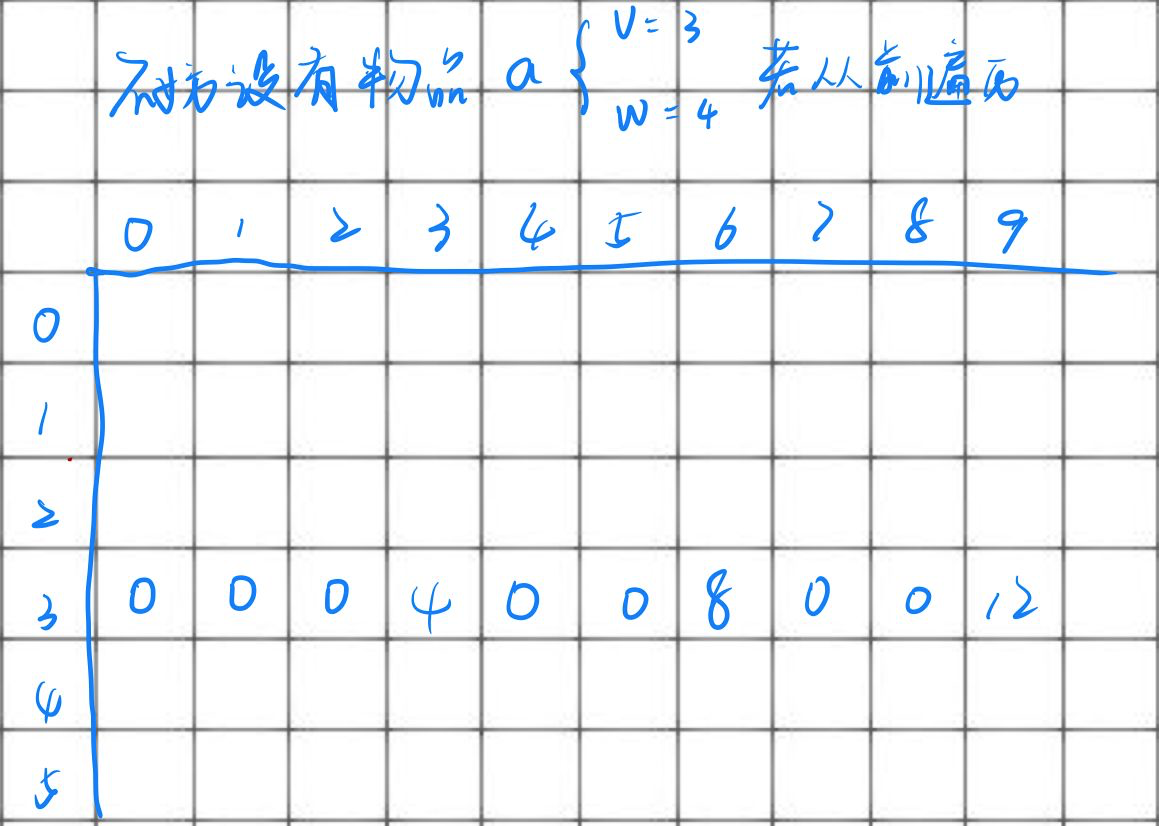
因为dp[6] = max(dp[6],dp[6 - 3] + w[3])，同理可知dp[9] = 12。不难发现，这样表示的含义就是每个物品都能放无限次，恰好符合完全背包的题目定义。

多重背包1⃣️

题目描述

有 N 种物品和一个容量是 V 的背包。

第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式

输出一个整数，表示最大价值。

样例

输入样例

4 5
1 2 3
2 4 1
3 4 3
4 5 2

输出样例：

10

我的代码

#include<iostream>
#include<math.h>
#define int long long
const int N = 1e3 + 5;
int dp[N];
signed main(){
    int V,n;
    std::cin >> n >> V;
    int v[n + 1],w[n + 1],s[n + 1];
    for(int i = 1;i <= n;i ++) {
        std::cin >> v[i] >> w[i] >> s[i];
    }
    for(int i = 1;i <= n;i ++){
        for(int k = 1;k <= s[i];k ++) {
            for (int j = V;j >= v[i] * k;j --) {
                dp[j] = std::max(dp[j], dp[j - v[i]]+ w[i]);
            }
        }
    }
    std::cout<<dp[V]<<"\n";
    return 0;
}

解题思路

不难发现是完全背包的一点点小变化的版本，从不限制个数到限制个数，只需要把完全背包的朴素版稍作修改就可以了。

蒟蒻被坑全过程：
本蒟蒻因为刚刚在01背包被坑了，所以记忆深刻，写完全背包的时候直接就想到了优化版，导致本蒟蒻好像并不会朴素版的完全背包。在自己搓多重背包的时候，把第二层循环和第三层循环写反了，wa了不知道多久之后，打开了神犇的blog（指路），抱着试试的心态，把位置换了一下，成功AC了，但是本蒟蒻人菜胆大，始终觉得先按个数放，再看剩余空间思路上没有问题，肯定是某个小细节没有考虑到！

One hour later……在神犇的提点下，本蒟蒻幡然醒悟。

回忆一下，当前消耗体积j下的最优的状态必定是由消耗体积j - v[i]的最优状态的转化来的，所以……第二层和第三层循环不能交换

好的，事情出现了转机。

在写……的部分的时候，我还是感觉怪怪的，就拿被我缝缝补补几次的代码出来，想跑一组数据来输出整个变化过程的表格，来看看到底在哪里出了问题。结果发现这组数据居然对了，交上去测评试了一下，居然AC了。所以我真的是有小细节没有考虑到：1、k必须从1开始，如果从0开始的话，k = 0时会全部被覆盖2、状态转移方程为：dp[j] = std::max(dp[j], dp[j - v[i]]+ w[i])而非dp[j] = std::max(dp[j], dp[j - v[i] * k]+ w[i] * k)

这里是本蒟蒻的调了不知道多久的代码

#include<iostream>
#include<math.h>
#define int long long
const int N = 1e3 + 5;
int dp[N];
signed main(){
    int V,n;
    std::cin >> n >> V;
    int v[n + 1],w[n + 1],s[n + 1];
    for(int i = 1;i <= n;i ++) {
        std::cin >> v[i] >> w[i] >> s[i];
    }
    for(int i = 1;i <= n;i ++){
        for(int k = 1;k <= s[i];k ++) {
            for (int j = V;j >= v[i] * k;j --) {
                dp[j] = std::max(dp[j], dp[j - v[i]]+ w[i]);
            }
        }
    }
    std::cout<<dp[V]<<"\n";
    return 0;
}

多重背包2⃣️

题目描述

有 N 种物品和一个容量是 V 的背包。

第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N≤1000
0<V≤2000
0<vi,wi,si≤2000

提示：

本题考查多重背包的二进制优化方法。

样例

输入样例

4 5
1 2 3
2 4 1
3 4 3
4 5 2

输出样例：

10

我的代码

#include<iostream>
#include<math.h>
#define int long long
const int N = 1e5 + 5;
int dp[N];
int v[N],w[N];
signed main(){
    int V,n;
    std::cin >> n >> V;
    int cnt = 0;
    for(int i = 1;i <= n;i ++){
        int a,b,s;
        std::cin >> a >> b >> s;
        int k = 1;
        while (k <= s){
            cnt ++;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if(s > 0){
            cnt ++;
            v[cnt] = a * s;
            w[cnt] = b * s;
            s -= s;
        }
    }
    for(int i = 1;i <= cnt;i ++){
        for (int j = V;j >= v[i];j --) {
            dp[j] = std::max(dp[j], dp[j - v[i]]+ w[i]);
        }
    }
    std::cout<<dp[V]<<"\n";
    return 0;
}

解题思路

刚开始完全没思路，看了神犇的题解都不理解什么意思，理解了好一会才知道啥意思，咱们这就重点以蒟蒻的视角，来解释一下，我们不妨设物品的体积为v，价值为w，
有a个，那么我们可以将a用二进制表示即a = 2 ^ 0 + 2 ^ 1 + 2 ^ 2 + .... + 2 ^ n + t(余数)，将其分别作为新的物品存储起来，代码上可以看得很清楚。不知道有没有萌新跟我一样，不理解这样分组是不是不能能覆盖到全部的情况。那我们画个表就清楚了！

可以看到如果当取3给为最优时，我们可以取a[0]和a[1]，因为2进制可以表示所有10进制的数，所以无论最优应该取几，都能由a拆分的数组组合而成，类似于01背包的操作。

后记

虽然还有其他的背包的内容，但是时间有限，背包的内容暂时告一段落啦，完结撒花🎉

如果有任何问题欢迎随时告诉我，感激不尽🌹