C++ 相关系数的计算以及在图像配准领域应用演示
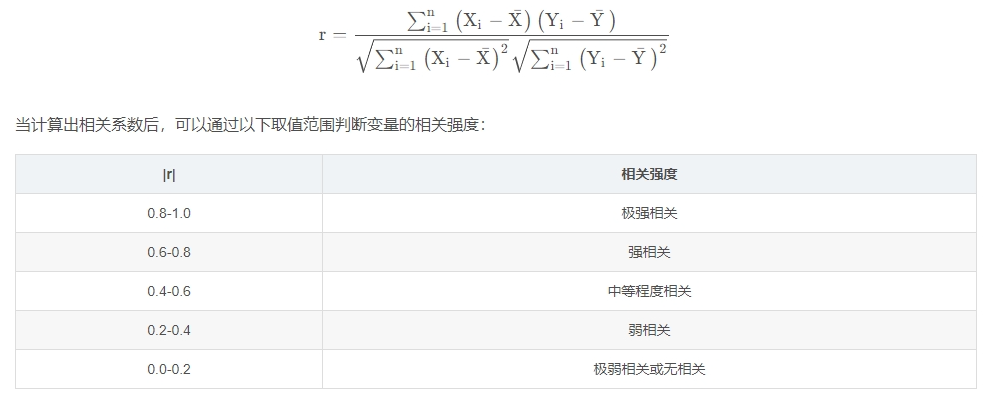
相关系数(皮尔逊相关系数)公式如下


#include <iostream> #include <vector> #include <cmath> using namespace std; // 计算平均值 double mean(vector<double> v) { double sum = 0; for (int i = 0; i < v.size(); i++) { sum += v[i]; } return sum / v.size(); } // 计算协方差 double covariance(vector<double> x, vector<double> y) { double x_mean = mean(x); double y_mean = mean(y); double sum = 0; for (int i = 0; i < x.size(); i++) { sum += (x[i] - x_mean) * (y[i] - y_mean); } return sum / x.size(); } // 计算相关系数 double correlation(vector<double> x, vector<double> y) { double cov = covariance(x, y); double x_std = sqrt(covariance(x, x)); double y_std = sqrt(covariance(y, y)); return cov / (x_std * y_std); } int main() { vector<double> x1 = { 2, 3, 4, 5, 6 }; vector<double> y1 = { 2, 3, 4, 5, 6 }; cout << "x1: "; for (int i = 0; i < x1.size(); i++) { cout << x1[i] << " "; } cout << endl; cout << "y1: "; for (int i = 0; i < y1.size(); i++) { cout << y1[i] << " "; } cout << endl; cout << "x1-y1相关系数: " << correlation(x1, y1) << "\r\n" << endl; vector<double> x2 = { 2, 3, 4, 5, 6 }; vector<double> y2 = { 20, 30, 40, 50, 60 }; cout << "x2: "; for (int i = 0; i < x2.size(); i++) { cout << x2[i] << " "; } cout << endl; cout << "y2: "; for (int i = 0; i < y2.size(); i++) { cout << y2[i] << " "; } cout << endl; cout << "x2-y2相关系数: " << correlation(x2, y2) << "\r\n" << endl; vector<double> x3 = { 2, 3, 4, 5, 6 }; vector<double> y3 = { 2, 3, 5, 6, 7 }; cout << "x3: "; for (int i = 0; i < x1.size(); i++) { cout << x3[i] << " "; } cout << endl; cout << "y3: "; for (int i = 0; i < y3.size(); i++) { cout << y3[i] << " "; } cout << endl; cout << "x3-y3相关系数: " << correlation(x3, y3) << "\r\n" << endl; vector<double> x4 = { 2, 3, 4, 5, 6 }; vector<double> y4 = { 6, 2, 5, 3, 4 }; cout << "x4: "; for (int i = 0; i < x4.size(); i++) { cout << x4[i] << " "; } cout << endl; cout << "y4: "; for (int i = 0; i < y4.size(); i++) { cout << y4[i] << " "; } cout << endl; cout << "x4-y4相关系数: " << correlation(x4, y4) << "\r\n" << endl; vector<double> x5 = { 2, 3, 4, 5, 6 }; vector<double> y5 = { 7, 6, 5, 4, 3 }; cout << "x5: "; for (int i = 0; i < x5.size(); i++) { cout << x5[i] << " "; } cout << endl; cout << "y5: "; for (int i = 0; i < y5.size(); i++) { cout << y5[i] << " "; } cout << endl; cout << "x5-y5相关系数: " << correlation(x5, y5) << "\r\n" << endl; return 0; }

相关系数越接近+1则两个向量同方向接近,相关系数越接近-1则两个向量反方向接近。该系数的应用举例 ---图像配准
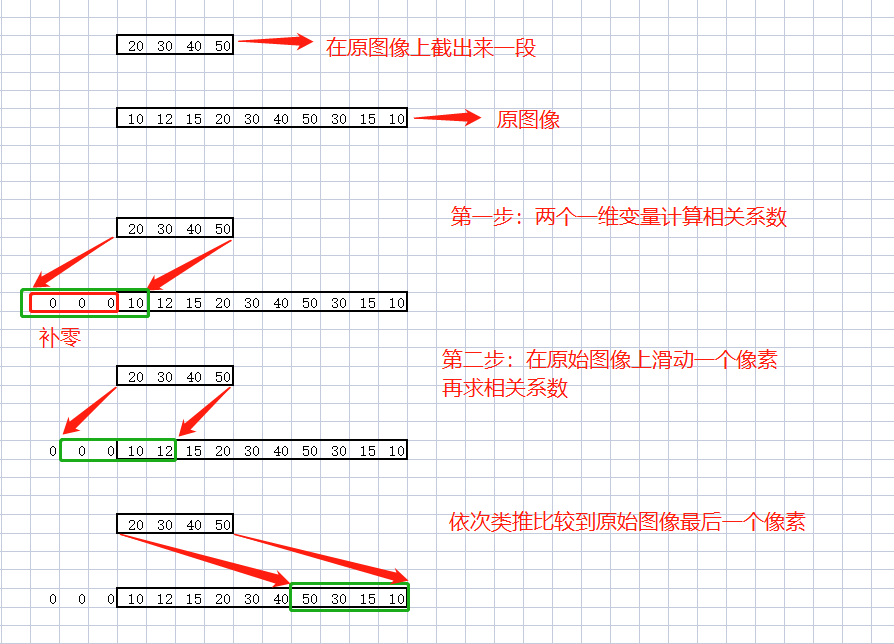
原始图像[ 10 12 15 20 30 40 50 30 15 10] 总共10个长度的像素,裁剪图像[ 20 30 40 50]总共4个长度的像素,在原始图像前补4 -1 个0,让裁剪图像依次从左到右得到 10 +4 -1 个长度的系数向量。在这个系数向量中找到最大的系数
本文引用
相关系数——皮尔逊相关系数的公式及其理解_胤风的博客-CSDN博客
