常用代码模板3——搜索与图论
常用代码模板3——搜索与图论
DFS
dfs没有模板,关键是搜索的顺序和剪枝
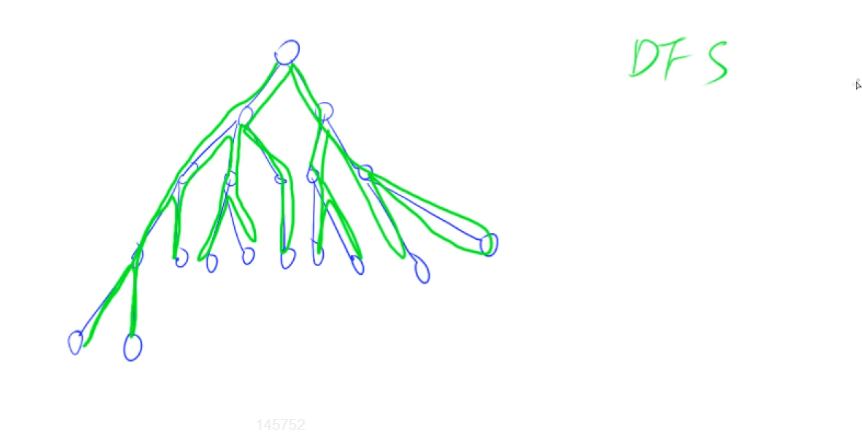
- 关键:搜索顺序
- 回溯、剪枝、搜索树
- 剪枝:最优性剪枝(当前路径一定不如最优解)、可行性剪枝
- 每次只存储一条搜索路径
- 处理的问题:对空间要求比较高,算法思路比较奇怪
…… dfs(int u, ……) // 到树的第几层和其他参数
{
// 剪枝
// 搜到叶节点后的逻辑
if(check(u))
{
}
// 搜索该节点的所有子节点
for (int i = 1; i <= n; i ++ )
{
if(check(i)) // 如果这个子节点可以走
{
store(u, i); // 存储路径
dfs(u+1); // 移动到下一层,搜索它的所有子节点
recover(i); // 该子节点下的所有路径搜完了,回溯并恢复现场
}
// 搜索下一个子节点
}
}
BFS
bfs图解
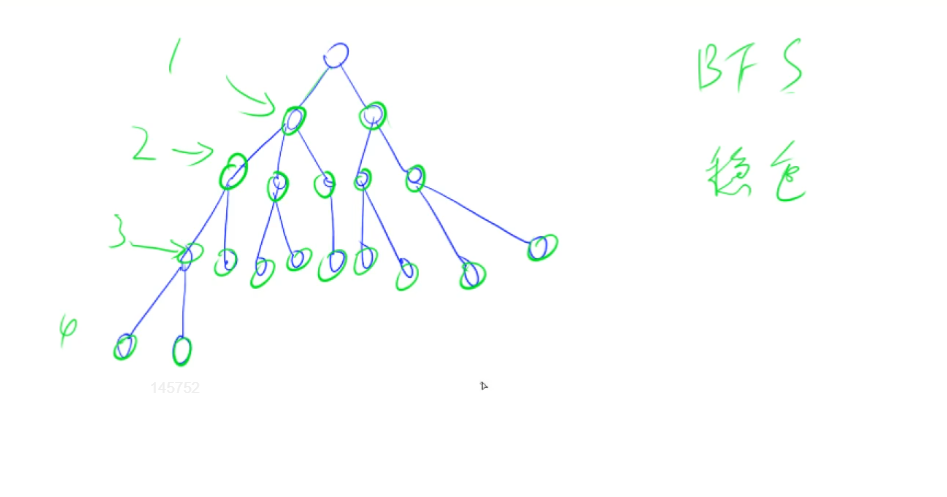
-
搜索顺序:搜索所有到起点距离为1的点 - > 搜索所有到起点距离为2的点 - > 搜索所有到起点距离为3的点 - > ……(距离为n的点是由距离为n-1的点走到的,而且之前没有走过)
-
当图中所有边的权重都是1时,bfs第一次搜到的一定是最短路,因为bfs是按到起点的距离向外搜索的,所以每个点第一次被搜到时一定是最短距离
-
存储路径的话定义一个pre数组,对于每个点,记录它是从哪个点走过来的
-
处理的问题:最小步数、最短路、最少操作次数
…… bfs()
{
// 初始状态可以把所有点的距离置为-1, 表示没走过
// memset(d, -1, sizeof(d))
// 然后将起点入队并更新它的距离为0
queue <- 初始状态
while (queue不空)
{
t <- 队头出队
t的所有邻点x入队(到t距离是1且没走过的点),d[x]=d[t]+1
}
}
树与图的存储
树是一种特殊的图(无环连通图),与图的存储方式相同。
对于无向图中的边ab,存储两条有向边a->b, b->a。
因此我们可以只考虑有向图的存储。
(1) 邻接矩阵:储存稠密图,g[a][b] 存储边a->b,a->b如果有多条边只能存一条
(2) 邻接表:储存稀疏图
// 对于每个点k,开一个单链表,存储k所有可以走到的点。h[k]存储这个单链表的头结点
// N不小于点的总数,M不小于边的总数
int h[N], e[M], ne[M], idx;
// 添加一条边a->b
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
// 初始化
idx = 0;
memset(h, -1, sizeof h);
树与图的遍历
时间复杂度 O(n+m), n表示点数,m表示边数
1. 深度优先遍历
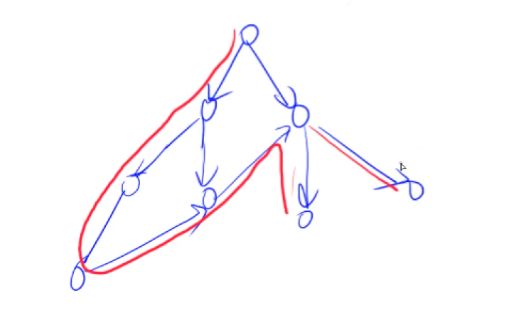
对于树,dfs可以维护子树信息
int dfs(int u) // u是当前搜到的点
{
st[u] = true; // st[u] 表示点u已经被遍历过
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j]) dfs(j);
}
}
2. 宽度优先遍历
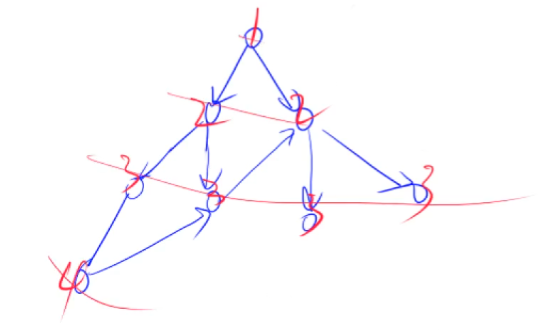
queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);
while (q.size())
{
int t = q.front();
q.pop();
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true; // 表示点j已经被遍历过
q.push(j);
}
}
}
拓扑排序
时间复杂度 O(n+m), n 表示点数,m 表示边数
// 递推的思想:如果要求一个图的拓扑序列,可以先找到一个入度为0的点并摘掉它,求剩余图的拓扑序列,再将该点放在开头即可得到原图的拓扑序列。最小问题(一个点就是它自身的拓扑序列)有解,
// 思路:先让所有入度为0的点入队,取队头并出队,遍历所有邻点,将由该点出发的边都删除,就相当于将这个点摘掉。然后在删的过程中,有邻点的入度减为零,则该邻点可以作为新图的起点,要入队。如果所有的点都入队了,说明每个新图都是有入度为0的点作为起点的(即有解),那么原问题一定有解,并且由于每个新图的起点都从队尾入队,则拓扑序列就存在队列中。
bool topsort()
{
int hh = 0, tt = -1;
// d[i] 存储点i的入度
for (int i = 1; i <= n; i ++ )
if (!d[i])
q[ ++ tt] = i;
while (hh <= tt)
{
int t = q[hh ++ ];
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (-- d[j] == 0)
q[ ++ tt] = j;
}
}
// 如果所有点都入队了,说明存在拓扑序列;否则不存在拓扑序列。
return tt == n - 1;
}
最短路算法
最短路问题
-
概念
- 源点:起点
- 汇点:终点
- n:点数
- m:边数
-
分类
-
单源最短路:从一个固定点到其他所有点的最短距离(如从1->n)
- 所有边权都是正数:
- 朴素dijkstra算法:复杂度\(O(n^2)\),与边数无关,适用于稠密图(点少边多),例如边数是\(n^2\)级别的。
- 堆优化版dijkstra算法:复杂度\(O(mlogn)\),适用于稀疏图(点和边一个级别或点多边少),例如点数和边数差不多时。
- 存在负权边:
- bellman-ford算法:复杂度\(O(nm)\),一般用于求不超过k条边的最短路
- spfa算法:一般\(O(m)\),最坏\(O(nm)\),如果对最短路经过的边数限制,只能用bellman-ford算法
- 所有边权都是正数:
-
多源汇最短路:求任意两个点之间的最短距离(起点不止一个)
floyd算法:复杂度\(O(n^3)\)
-
-
关键:建图(将原问题抽象成最短路),如何定义点和边,不侧重于证明算法的正确性
dijkstra算法(无负权边)
1. 朴素dijkstra算法(稠密图)
时间复杂是 \(O(n^2)\), n 表示点数
步骤:(这里的距离指的都是到出发点的距离)
-
起点的距离置为0,其他点的距离置为\(\infty\)
-
每次从未标记的节点中选择距离最小的节点赋给 t ,并把这个点标记,收录到最短路径集合中(基于贪心算法,没有确定最短路的、距离出发点最近的点此时的距离就是它的最短距离)
-
用 t 更新邻点的距离,若(节点 t 的距离 + 节点 t 到该节点的边长)<该节点的距离,就更新该节点的距离
由于 :
1. 已经确定最短路的点的距离一定最小 2. 与 t 不连通的点一定与起点不连通,$g[t][j]=dist[j]=\infty<dist[t]+g[t][j]=dist[t]+\infty$所以直接遍历所有点即可
每一次循环确定一个点的最短距离,循环 n - 1 次是因为最后一个点只更新了距离并且已经确定是最短距离,所以不需要再考虑加入st[n]的操作
重边保留长度最短的那条,自环不影响(在更新距离时,如果遍历到自己,dist[t] < dist[t] + g[t][t],所以dist[t]不变)
int g[N][N]; // 存储每条边
int dist[N]; // 存储1号点到每个点的最短距离
bool st[N]; // 存储每个点的最短路是否已经确定
memset(g, 0x3f, sizeof(g)); // 每条边初始化为正无穷
// 求1号点到n号点的最短路,如果不存在则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n - 1; i ++ )
{
int t = -1; // 在还未确定最短路的点中,寻找距离最小的点
for (int j = 1; j <= n; j ++ )
{
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
}
st[t] = true; // 把这个点标记,收录到最短路径集合中
// 用t更新其他点的距离
for (int j = 1; j <= n; j ++ )
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
2. 堆优化版dijkstra (稀疏图)
时间复杂度 O(mlogn), n 表示点数,m 表示边数
步骤:(这里的距离指的都是到出发点的距离)
- 起点的距离置为0,其他点的距离置为\(\infty\)
- 用小根堆来维护距离最小的点,由于一个点会进堆入度次,则已经确定最短路的可能在堆顶,每次取堆顶后赋给 t 后要判断,直到取到未确定最短路的、距离最小的点,并把这个点标记,收录到最短路径集合中。
- 用 t 更新它的邻点的距离,若(节点 t 的距离 + 节点 t 到该节点的边长)<该节点的距离,就更新该节点的距离,并将该距离进堆。
typedef pair<int, int> PII;
int n; // 点的数量
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边,w[]储存边长
int dist[N]; // 存储所有点到1号点的距离
bool st[N]; // 存储每个点的最短距离是否已确定
// 加边,带权
void add(int a, int b, int c)
{
e[idx]=b, w[idx]=c, ne[idx]=h[a], h[a]=idx++;
}
// 求1号点到n号点的最短距离,如果不存在,则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1}); // first存储距离,second存储节点编号,因为pair优先比较first
// 堆空时所有与起点连通的点的最短路已经被算出来了
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({dist[j], j});
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}
Bellman-Ford算法(有负权边)
时间复杂度 O(nm), n 表示点数,m 表示边数
注意在模板题中需要对下面的模板稍作修改,加上备份数组,详情见模板题。
三角不等式:\(dist[b] \leq dist[a] + w\)
松弛操作:\(dist[b] = dist[a] + w\)
循环k次后dist[]的意义:从起点经过不超过k条边到达该点的最短距离(如果发生串联则不是,所以需要一个backup[]数组备份上一次迭代的结果,松弛操作用backup[]更新)
如果图中存在负权回路,最短路不一定存在,若负环不在路径上,则不影响
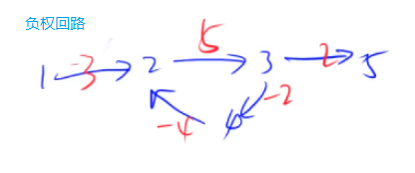
步骤:
- 起点的距离置为0,其他点的距离置为\(\infty\)
- 循环k次(k为允许经过的最大边数),每次对所有边都进行松弛操作\(dist[b] = dist[a] + w\)
- 循环结束之后,dist中存的就是最短路
注意:与起点不连通的点也可能被更新,所以要用dist[i] > inf / 2判断,并且不存在要返回inf,不是-1
int n, m; // n表示点数,m表示边数
int dist[N]; // dist[x]存储1到x的最短路距离
struct Edge // 边,a表示出点,b表示入点,w表示边的权重
{
int a, b, w;
}edges[M];
// 求1到n的最短路距离,如果无法从1走到n,则返回-1。
int bellman_ford()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
// 如果第n次迭代仍然会松弛三角不等式,就说明存在一条长度是n+1的最短路径,由抽屉原理,路径中至少存在两个相同的点,说明图中存在回路。由于经过n+1条边的dist比经过n条边的dist短,说明该回路一定是负权回路。
// 循环n次表示经过n条边(不判断负环可改为n-1,因为只有n-1条边)
for (int i = 0; i < n; i ++ )
{
// 对每条边都进行松弛操作
for (int j = 0; j < m; j ++ )
{
auto t = edge[j];
dist[t.b] = min(dist[t.b], dist[t.a] + t.w);
}
}
if (dist[n] > 0x3f3f3f3f / 2) return 0x3f3f3f3f;
return dist[n];
}
// if(bellman_ford()==0x3f3f3f3f) 不存在最短路
// else 存在
spfa 算法(队列优化的Bellman-Ford算法)(无负环)
时间复杂度 平均情况下 O(m),最坏情况下 O(nm), n 表示点数,m 表示边数
因为松弛操作:\(dist[b] = dist[a] + w\)中\(dist[b]\)要减小就要求\(dist[a]\)减小,所有可以用一个队列存储所有变小的的点(要判重),当队列空的时候,迭代也不会改变dist[]的值,退出。
步骤:
- 起点的距离置为0,其他点的距离置为\(\infty\)
- 起点入队,打上标记
- 当队列不空时,取队头,去除标记,并用队头松弛所有邻边,并将成功松弛的点入队,打上标记
int n; // 总点数
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N]; // 存储每个点到1号点的最短距离
bool st[N]; // 存储每个点是否在队列中
// 求1号点到n号点的最短路距离,如果从1号点无法走到n号点则返回-1
int spfa()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
if (!st[j]) // 如果队列中已存在j,则不需要将j重复插入
{
q.push(j);
st[j] = true;
}
}
}
}
return dist[n];
}
// if(spfa() == 0x3f3f3f3f) 不存在最短路
// else 存在
spfa判断图中是否存在负环
时间复杂度是 O(nm), n 表示点数,m 表示边数
spfa判负环有两种做法,去掉st数组会更快
- bfs做法:(较慢)
int n; // 总点数
int h[N], w[N], e[N], ne[N], idx; // 邻接表存储所有边
int dist[N], cnt[N]; // dist[x]存储1号点到x的最短距离,cnt[x]存储1到x的最短路中经过的点数
bool st[N]; // 存储每个点是否在队列中,可以不用
// 如果存在负环,则返回true,否则返回false。
bool spfa()
{
// 不需要初始化dist数组,当dist初始值为0时,代码会在负环处打转(负环内元素一直入队出队,cnt[]单调递增直到>=n)
// 原理:如果某条最短路径上有n个点(除了自己),那么加上自己之后一共有n+1个点,由抽屉原理一定有两个点相同,所以存在环。
queue<int> q;
// 把所有点都放在初始点集中,防止有从1号点到不了的负环
for (int i = 1; i <= n; i ++ )
{
q.push(i);
st[i] = true;
}
while (q.size())
{
auto t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
dist[j] = dist[t] + w[i];
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return true; // 如果从1号点到x的最短路中包含至少n个点(不包括自己),则说明存在环,且为负环(路更长距离反而更短)
if (!st[j])
{
q.push(j);
st[j] = true;
}
}
}
}
return false;
}
-
dfs做法:(较快,注意dist一定要初始化为0)
只需将bfs中的队列换成栈即可。
floyd算法 (无负环)
时间复杂度是 O(\(n^3\)), n 表示点数
重边取最短的,自环忽略
d[N][N]; // 邻接矩阵
初始化:
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
if (i == j) d[i][j] = 0;
else d[i][j] = INF;
// 算法结束后,d[a][b]表示a到b的最短距离
void floyd()
{
// 一定要先循环k
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
// if(d[a][b] > INF / 2) 不存在最短路
// else 存在
最小生成树算法
一般是无向图,要同时加a->b,b->a两条边
朴素版prim算法(稠密图)
时间复杂度是\(O(n^2)\),n 表示点数,m 表示边数
步骤:(距离:点到集合内点的所有连线中的最短长度)
- 将所有点的距离初始化为\(+\infty\)
- 每次找到最小生成树集合外的距离最近的点赋给 t ,并将它标记,收录到最小生成树集合中
- 用 t 更新其他点的距离。如果该点到 t 的距离比当前该点到集合的距离短,就将该点的到集合的距离更新为到 t 的距离
每一次循环都将一个点加入最小生成树中,循环 n 次即可
重边保留长度最短的那条,自环会有影响,要先将新的树边长度加入权重之和中,再更新距离,否则dist[t] = min(dist[t], g[t][t])中,自环可能会修改dist[t],导致树边长度不正确
int n; // n表示点数
int g[N][N]; // 邻接矩阵,存储所有边
int dist[N]; // 存储其他点到当前最小生成树的距离
bool st[N]; // 存储每个点是否已经在生成树中
memset(g, 0x3f, sizeof(g)); // 每条边初始化为正无穷
g[a][b] = g[b][a] = min(g[a][b], w); // 重边取最短,如果是无向图要加两条边
// 如果图不连通,则返回INF(值是0x3f3f3f3f), 否则返回最小生成树的树边权重之和
int prim()
{
memset(dist, 0x3f, sizeof dist);
int res = 0;
for (int i = 0; i < n; i ++ )
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
if (i && dist[t] == INF) return INF; // 当前不是第一个点(如果是第一个点dist还没更新,一个点也不能谈连通)且距离集合最短的点都是INF,说明图不连通,不存在最小生成树
if (i) res += dist[t]; // 如果不是第一个点,当前的dist[t]就是距离最短的点到集合的距离,是一条树边,注意这一步要在更新距离之前,防止自环
st[t] = true;
for (int j = 1; j <= n; j ++ )
dist[j] = min(dist[j], g[t][j]); // 可能会修改集合内点的dist,可以加个判断if(!st[j])
}
return res;
}
// 更简洁的写法
int prim()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0; // 规定一号点是起点,将它的dist提前置成0,可以减少特判
int res = 0;
for (int i = 0; i < n; i ++ )
{
int t = -1;
for (int j = 1; j <= n; j ++ )
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
if (dist[t] == INF) return INF; // 一号点是0,不会return
st[t] = true;
res += dist[t]; // 一号点的dist是0,放心加
for (int j = 1; j <= n; j ++ )
dist[j] = min(dist[j], g[t][j]);
}
return res;
}
Kruskal算法(稀疏图)
时间复杂度是\(O(mlogm)\),n 表示点数,m 表示边数
步骤:
- 将所有边按权重从小到大排序。
- 枚举每条边a-b,权重c,如果a, b不在一个连通块(并查集维护),将这条边加入最小生成树集合中,并将a,b这两个连通块合并
重边、自环不影响
理解:将所有的边升序排列,从小到大遍历的过程中,每次都以最小的代价将两个点连通,如果这两个点已经连通,说明在之前已经用更小的代价将它们连通了。像这样,每个点的连通都是最优解,如果存在最小生成树,一定可以找到n - 1条边,保证每条边都是最优解,那么最终的权重之和就是最优解。如果找不到,说明不存在最小生成树。
int n, m; // n是点数,m是边数
int p[N]; // 并查集的父节点数组,用并查集来维护连通块
struct Edge // 存储边
{
int a, b, w;
bool operator< (const Edge &W)const
{
return w < W.w;
}
}edges[M]; // M不小于总边数
int find(int x) // 并查集核心操作
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int kruskal()
{
sort(edges, edges + m);
for (int i = 1; i <= n; i ++ ) p[i] = i; // 初始化并查集
int res = 0, cnt = 0; // res是最小生成树的树边权重之和,cnt是当前最小生成树集合中的边数
for (int i = 0; i < m; i ++ )
{
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
a = find(a), b = find(b);
if (a != b) // 如果两个连通块不连通,则将这两个连通块合并,并将这条边加入最小生成树集合中
{
p[a] = b;
res += w;
cnt ++ ;
}
}
if (cnt < n - 1) return INF; // 如果边数小于n-1条,说明图不连通,不存在最小生成树
return res;
}
染色法判别二分图
时间复杂度是\(O(n+m)\),n 表示点数,m 表示边数

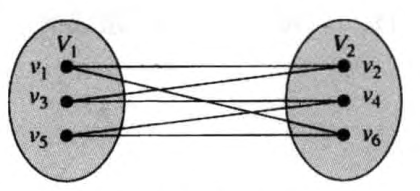
步骤:
- 将所有点置为未染色状态
- 遍历每个点,如果该点未染色,就以它为起点染色,如果返回了false,则不是二分图
- 染色:先将当前点染色,再遍历子节点。如果子节点未染色,则递归以它为起点染色,并检查返回值;如果子节点已经染色了,则判断是否同色,如果同色则不是二分图。
int n; // n表示点数
int h[N], e[M], ne[M], idx; // 邻接表存储图
int color[N]; // 表示每个点的颜色,-1表示未染色,0表示白色,1表示黑色
// 参数:u表示当前节点,c表示当前点的颜色
// 是二分图返回true, 不是返回false
bool dfs(int u, int c)
{
color[u] = c;
for (int i = h[u]; i != -1; i = ne[i])
{
int j = e[i];
if (color[j] == -1)
{
if (!dfs(j, !c)) return false;
}
else if (color[j] == c) return false;
}
return true;
}
bool check()
{
memset(color, -1, sizeof color);
bool flag = true;
// 尝试把所有点作为染色的起点,防止图不连通
for (int i = 1; i <= n; i ++ )
if (color[i] == -1)
if (!dfs(i, 0))
{
flag = false;
break;
}
return flag;
}
匈牙利算法
时间复杂度是\(O(nm)\),n 表示点数,m 表示边数,实际运行时间一般远小于\(O(nm)\)
二分图的匹配:给定一个二分图 G,在 G 的一个子图 M 中,M 的边集 {E} 中的任意两条边都不依附于同一个顶点,则称 M 是一个匹配。(即没有两条边共用一个点)
二分图的最大匹配:所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
步骤:
对于每一个find,遍历该点的子节点,如果该子节点没被标记,就标记它。如果该子节点已经有匹配的节点了,就递归调用find,看能否为该子节点的匹配对象找到新的匹配,如果可以,就匹配该子节点,返回成功。如果所有的子节点都无法匹配,就返回失败。
int n1, n2; // n1表示第一个集合中的点数,n2表示第二个集合中的点数
int h[N], e[M], ne[M], idx; // 邻接表存储所有边,匈牙利算法中只会用到从第一个集合指向第二个集合的边,所以这里只用存一个方向的边
int match[N]; // 存储第二个集合中的每个点当前匹配的第一个集合中的点是哪个
bool st[N]; // 表示第二个集合中的每个点是否已经被遍历过
bool find(int x)
{
for (int i = h[x]; i != -1; i = ne[i])
{
int j = e[i];
if (!st[j])
{
st[j] = true;
if (match[j] == 0 || find(match[j]))
{
match[j] = x;
return true;
}
}
}
return false;
}
// 求最大匹配数,依次枚举第一个集合中的每个点能否匹配第二个集合中的点
int res = 0;
for (int i = 1; i <= n1; i ++ )
{
memset(st, false, sizeof st);
if (find(i)) res ++ ;
}
网络流
参考资料
0x3f的网络流笔记
算法学习笔记(28): 网络流 - 知乎 (zhihu.com)
最大流 - OI Wiki (oi-wiki.org)
网络流的基本概念




最大流
存图方式
链式前向星
优点:容易取反向边。当反向边紧接着正向边建立,且正向边的编号是偶数时,可以通过^1互相取到。
// N是最大点数,M是题目中所给的最大边数,inf是流的最大值,要大于所有容量值
const int N = 210, M = 5010, inf = 0x3f3f3f3f;
// 链式前向星存图
// 所谓链式前向星存的是边,to是该边指向的点(终点),c是该边的容量,ne是下一条与该边起点相同的边的编号。因为要建反向边,所以最大边数等于题目边数*2
struct Edge {ll to, c, ne;} edge[M * 2];
// h[i]存的i的第一条出边的编号,之后可以通过edge里的ne找到以i为起点的所有边
// add函数中使用idx++且以0为边界,所以idx从2开始
// 这样的好处是在定义是直接初始化,不需要在main函数里再初始化h为-1了
int h[N], idx = 2; // 从2,3开始配对
// mf[i]存S~i的流量上限,pre[i]存i的前驱边的编号
ll mf[N], pre[N];
// 遍历u的所有出边
for (int i = h[u]; i; i = edge[i].ne) // 0为边界
{
auto to = edge[i].to, cap = edge[i].c;
...
}
// 增加一条a->b,容量是c的边,同时建它的反向边
void add(int a, int b, int c)
{
// 这样赋值时变量的顺序要对应
edge[idx] = {b, c, h[a]}, h[a] = idx ++ ;
edge[idx] = {a, 0, h[b]}, h[b] = idx ++ ;
}
-
当链式前向星的模板中每次加边用的下标是当前的idx(即idx++),要把idx初始化为偶数。
idx初始为0,则边界是-1;idx初始为2,边界是0或-1。
-
当链式前向星的模板中每次加边用的下标是当前的idx+1(即++idx),要把idx初始化为奇数idx初始为-1,边界是-1;idx初始为1,边界是0或-1。
FF方法
算法学习笔记(28): 网络流 - 知乎 (zhihu.com)
找最大流算法的基本思想
// 维护残留网络
ans初始为0,每次找到一条增广路,由|f+f'|=|f|+|f'|,ans+=增广路流量
最终ans就是最大流的流量值
dfs 找增广路
{
找增广路径(找一条从s出发沿着容量大于0的边走到t的通路),并计算它的流量
更新残留网络 // 规定与流量同向的容量是正向,正向容量-流量,反向容量+流量
返回流量
}
while (dfs能找到一条增广路)
{
ans += 流量
}
Ford-Fulkerson算法具体的代码实现(from Pecco)
EK算法
EK:1e3~1e4(点数加边数)最大流不用,最小费用流用
y总的EK模板
董晓算法的EK模板
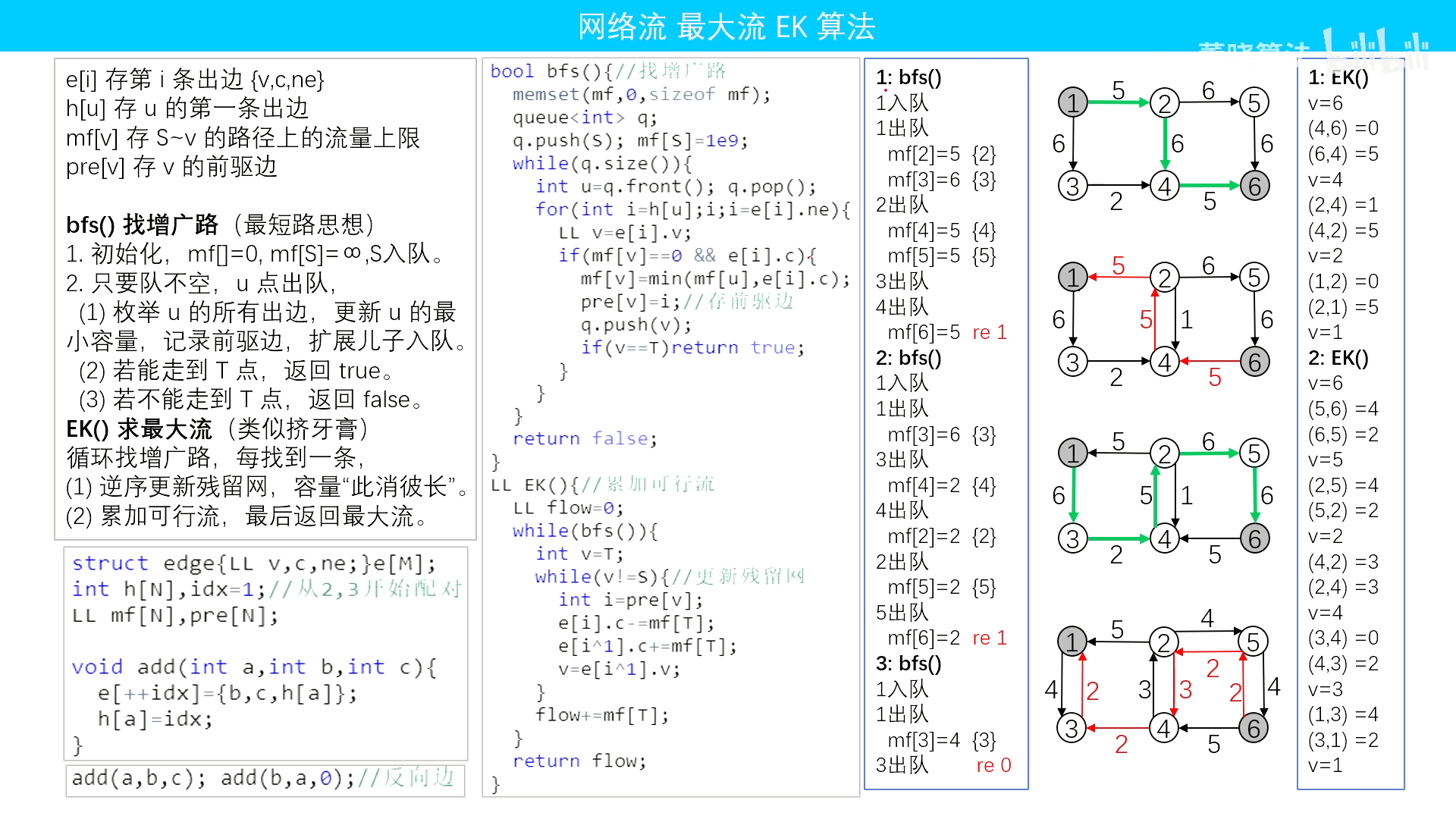
模板题:模板-网络最大流 草地排水
// 这是我结合多个模板写出的模板
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int N = 210, M = 5010, inf = 0x3f3f3f3f;
struct Edge {ll to, c, ne;} edge[M * 2];
int h[N], idx = 2;
ll mf[N], pre[N];
int n, m, S, T;
void add(int a, int b, int c)
{
edge[idx] = {b, c, h[a]}, h[a] = idx ++ ;
edge[idx] = {a, 0, h[b]}, h[b] = idx ++ ;
}
bool bfs()
{
// 每次寻找增广路前,初始化所有点的流量上限为0,这也是该点有没有走过的依据
memset(mf, 0, sizeof mf);
queue<int> q;
q.push(S), mf[S] = inf; // 源点入队,假设流量是正无穷
while (q.size())
{
// 每次遍历u的所有出边
auto u = q.front();
q.pop();
for (int i = h[u]; i; i = edge[i].ne)
{
auto to = edge[i].to, cap = edge[i].c;
// 如果该边的终点没走过且该边容量大于0
if (!mf[to] && cap)
{
mf[to] = min(mf[u], cap); // 计算能到达该边终点的流量上限
pre[to] = i; // 存该边终点的前驱边,也就是现在遍历到的这条边
q.push(to); // 终点入队
if (to == T) return true; // 如果已经找到汇点,返回true
}
}
}
return false; // 从源点走不到汇点,返回false
}
ll EK()
{
ll maxflow = 0; // 存最大流的流量
while (bfs()) // 当能找到一条增广路径时
{
// 新的可行流的流量等于原来的加上残留网络中增广路径的流量
maxflow += mf[T];
// 更新残留网络
// 遍历增广路上的每个点,
// 它的前驱边的容量-=流量,前驱边的反向边的容量+=流量
for (int i = T; i != S; i = edge[pre[i] ^ 1].to)
{
edge[pre[i]].c -= mf[T]; // pre[i]为i的前驱边编号
edge[pre[i] ^ 1].c += mf[T]; // pre[i]^1为i的前驱边反向边编号
// i的前一个点就是前驱边反向边的指向的点
}
}
return maxflow;
}
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m >> S >> T;
for (int i = 0; i < m; i ++ )
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
cout << EK();
return 0;
}
Dinic算法
Dinic:1e4~1e5(点数加边数)代码短
Dinic - OI Wiki
董晓算法讲解视频
y总的Dinic模板
董晓算法的Dinic模板
ISAP:和Dinic效率差不多,代码比Dinic长

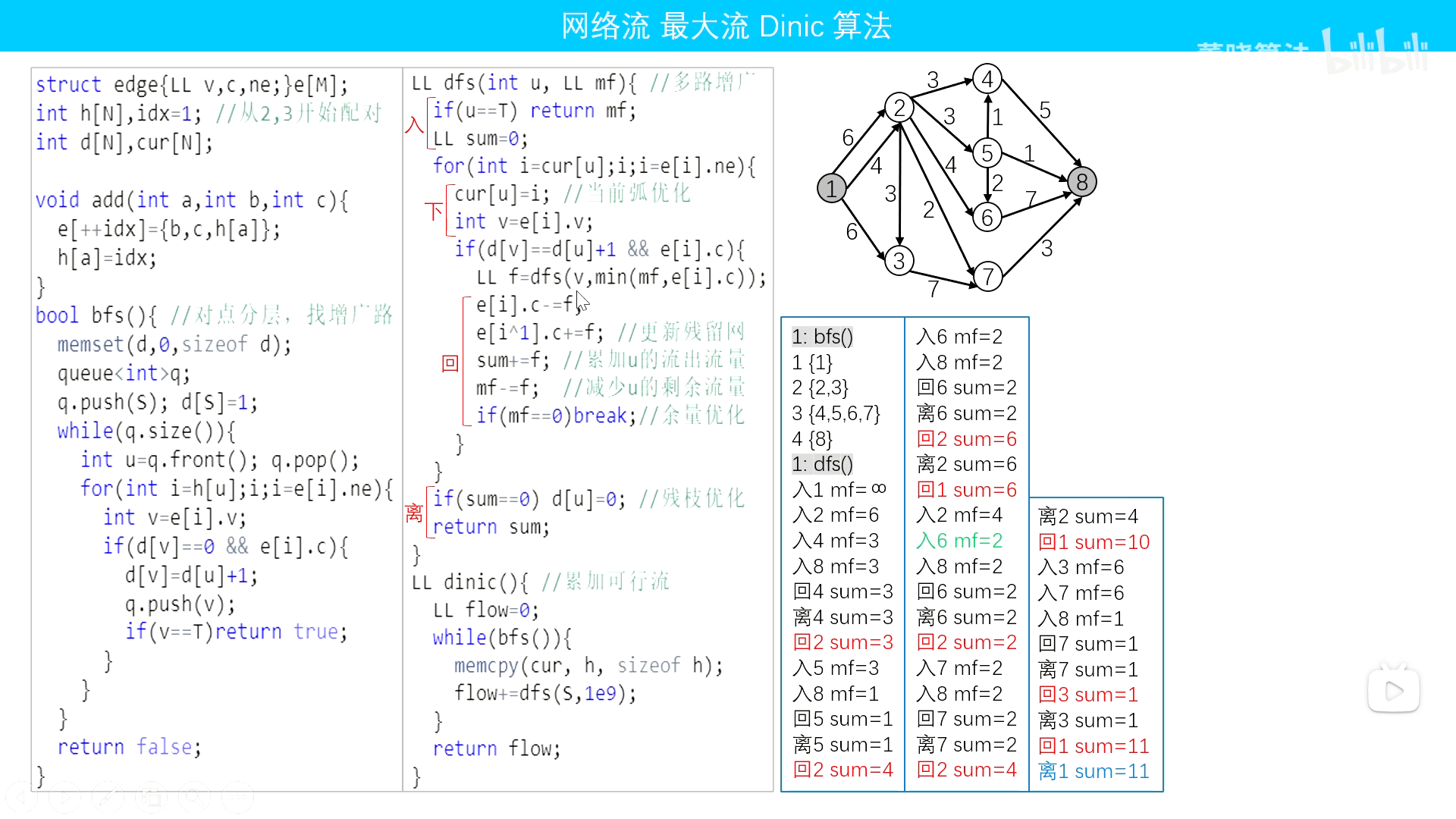

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int N = 210, M = 5010, inf = 0x3f3f3f3f;
struct Edge {ll to, c, ne;} edge[M * 2];
int h[N], idx = 2;
int d[N], cur[N]; // d[]存点的深度,cur存每个点的当前弧
int S, T, n, m;
void add(int a, int b, int c)
{
edge[idx] = {b, c, h[a]}, h[a] = idx ++ ;
edge[idx] = {a, 0, h[b]}, h[b] = idx ++ ;
}
// 对点分层,找增广路
bool bfs()
{
memset(d, 0, sizeof d);
queue<int> q;
q.push(S), d[S] = 1;
while (q.size())
{
auto u = q.front();
q.pop();
for (int i = h[u]; i; i = edge[i].ne)
{
auto to = edge[i].to, cap = edge[i].c;
if (!d[to] && cap)
{
d[to] = d[u] + 1;
q.push(to);
if (to == T) return true;
}
}
}
return false;
}
// 返回u在这一轮的网络结构以及流量上限是mf的情况下,从S~u~T的增广路流量之和
// 若u的高一层邻点是V,由S~u~T的增广路流量之和=把u分配给每个邻点v的流量是mf'的条件下,所有的邻点v的增广路流量之和累加的结果
ll dfs(int u, ll mf)
{
if (u == T) return mf;
ll sum = 0;
// 从当前弧开始
for (int i = cur[u]; i; i = edge[i].ne)
{
cur[u] = i; // 当前弧是为下一次再搜到u准备的,上一次搜到时已经搜索过u的前i-1条出边了,这些边已经增广到极限了(边 (u,v)已无剩余容量或 v的后侧已增广至阻塞),则 u的流量没有必要再尝试流向出边 (u,v)。而是从i开始尝试。
// 两种情况
// 1. 从这条边返回的f=mf,则说明v后面的边的容量都>=mf,则这条边i还有尝试的价值,此时mf=0,break,cur[u]就是i
// 2. f<mf,说明v后面存在容量小于mf的边集L,则L经过这次搜索容量已经减为0了,i的后侧阻塞,没有尝试的价值,此时mf>0,cur[u]之后会更新
auto to = edge[i].to, cap = edge[i].c;
if (d[to] == d[u] + 1 && cap)
{
ll f = dfs(to, min(mf, cap)); // 分配min(mf,cap)时,邻点v的增广路流量之和
edge[i].c -= f, edge[i ^ 1].c += f; // 更新残留网络
sum += f, mf -= f; // 累加u的流出流量,减少u的剩余流量
if (!mf) break; // 余量优化,如果u已经没有流量可分配了,就退出
}
}
if (!sum) d[u] = 0; // 如果从u到T的流量是0,说明u和T不连通,直接将u从图中去掉(残枝优化)
return sum;
}
ll dinic()
{
ll maxflow = 0;
while (bfs()) // 当存在增广路时
{
memcpy(cur, h, sizeof h); // 每一轮的网络结构不同,当前弧要从头开始
maxflow += dfs(S, inf); // 每一轮能找到的所有增广路径流量之和累加
}
return maxflow;
}
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m >> S >> T;
for (int i = 0; i < m; i ++ )
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
cout << dinic();
return 0;
}
最详细(也可能现在不是了)网络流建模基础 - victorique
在所有的最大流中寻找费用最小的,费用等于每条边的边权*流量累加 模板题: https://www.luogu.com.cn/problem/P3381 https://loj.ac/p/102 值:最小割=最大流 方案:我们找到了最大流,根据最大流最小割定理,它的值也就是最小割,因此当我们找到了最大流,也就是没有s->t的增广路径时,剩下的残留网络刚好将S集合与T集合分割开来,这就是最小割。寻找最小割对应边也就十分简单了: 原理:最大流的流量=最小割的容量,则在原网络中,S到T的边都是满流的,那么在最大流对应的残留网络(即最后的网络)中,这些边的容量都是0,也就是说,容量为0的边将S和T分隔。从s沿残留容量大于0的边能走到的都是S,都不到的都是T费用流
概念
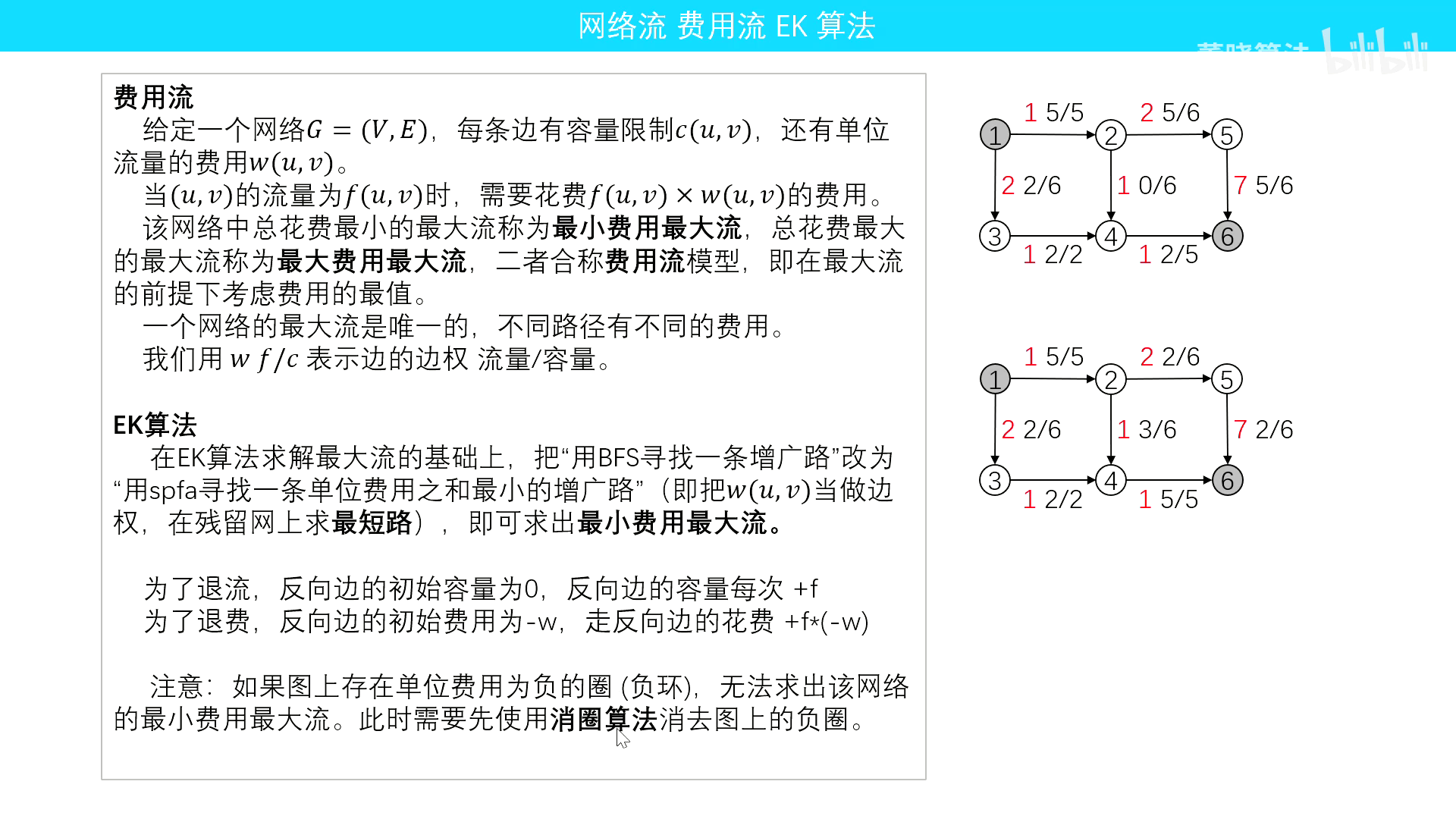
EK算法
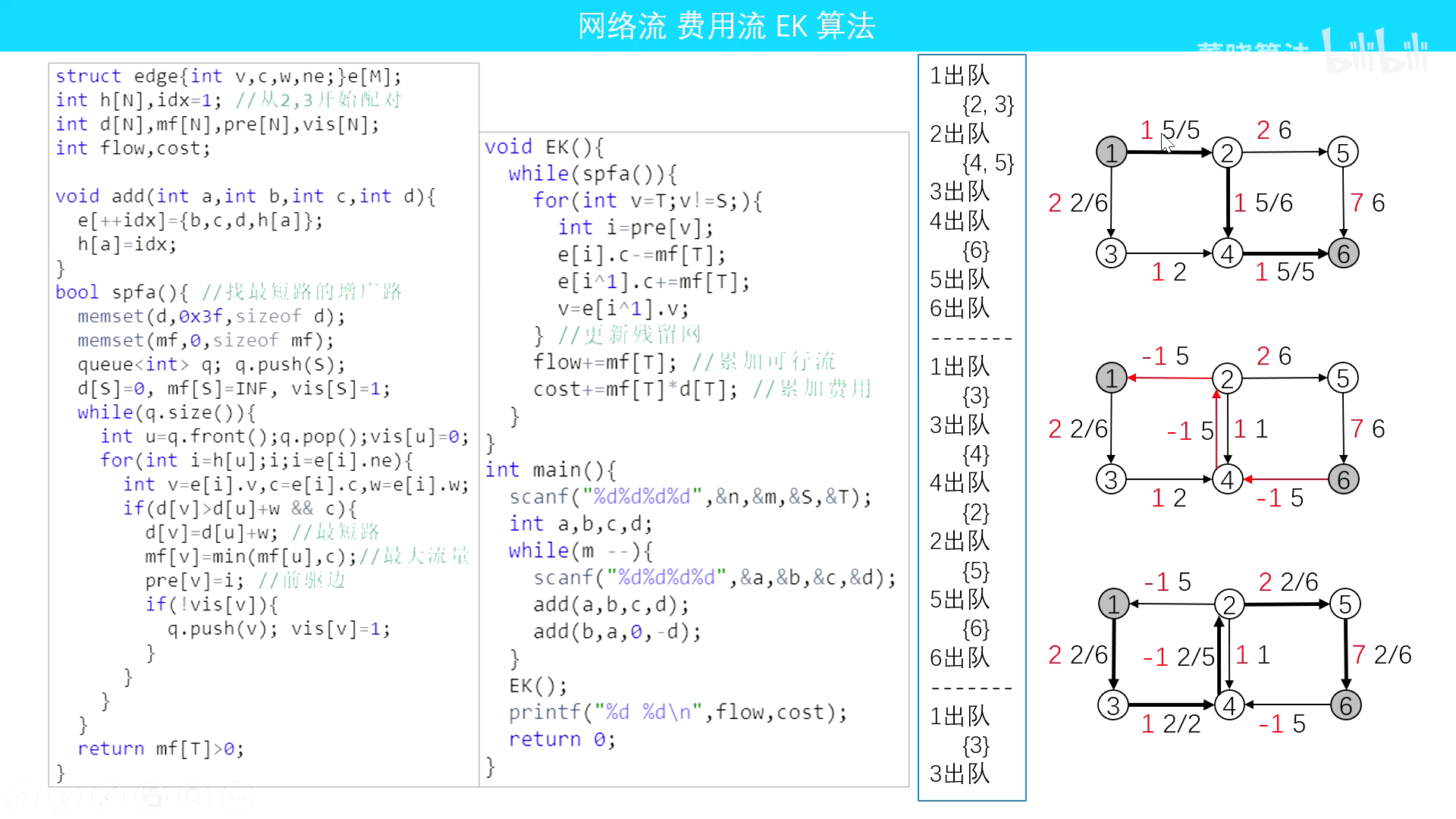
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int N = 5e3 + 10, M = 5e4 + 10, inf = 0x3f3f3f3f;
struct Edge {int to, c, w, ne; } edge[M * 2];
int h[N], idx = 2;
int mf[N], d[N], pre[N]; // d[]数组存每个点到源点的距离
bool vis[N]; // vis数组-spfa中使用
int n, m, S, T;
int maxflow, mincost; // 答案
void add(int a, int b, int c, int w)
{
edge[idx] = {b, c, w, h[a]}, h[a] = idx ++ ;
// 反向边初始容量为0,费用等于正向边的相反数
edge[idx] = {a, 0, -w, h[b]}, h[b] = idx ++ ;
}
bool spfa() // 寻找最短增广路
{
memset(mf, 0, sizeof mf);
memset(d, 0x3f, sizeof d);
queue<int> q;
q.push(S), vis[S] = 1, d[S] = 0, mf[S] = inf;
while (q.size())
{
auto t = q.front();
q.pop();
vis[t] = false;
for (int i = h[t]; i; i = edge[i].ne)
{
auto e = edge[i];
if (d[e.to] > d[t] + e.w && e.c) // 如果可以松弛且这条边的容量大于0,则该点入队
{
d[e.to] = d[t] + e.w;
mf[e.to] = min(mf[t], e.c);
pre[e.to] = i;
if (!vis[e.to]) q.push(e.to), vis[e.to] = true;
}
}
}
return mf[T] > 0;
}
void EK()
{
while (spfa())
{
maxflow += mf[T];
mincost += mf[T] * d[T]; // 增广路的费用=流量*路径长度
for (int i = T; i != S; i = edge[pre[i] ^ 1].to)
{
edge[pre[i]].c -= mf[T];
edge[pre[i] ^ 1].c += mf[T];
}
}
}
int main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
cin >> n >> m >> S >> T;
for (int i = 0; i < m; i ++ )
{
int a, b, c, w;
cin >> a >> b >> c >> w;
add(a, b, c, w);
}
EK();
cout << maxflow << ' ' << mincost;
return 0;
}
最小割
max_flow