2023.6.18拷逝
T1
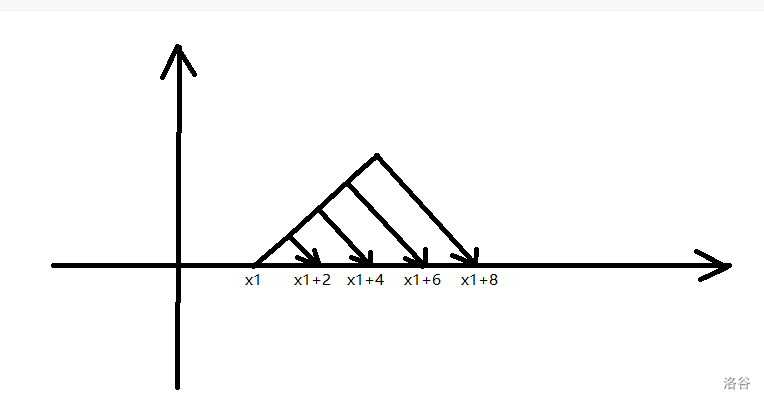
如图,从 \(x_1\) 能且只能走到 \(x_1+2,x_1+4,x_1+6...\)
设 \(f[x]\) 表示从 \(x_1\) 走到 \(x\) 的方案数,那么如果 \(x-x_1\) 是偶数,那么 \(f[x]=f[x-2]+f[x-4]+...+f[x_1]\) ,否则 \(f[x]=0\) 。初始值: \(f[x_1]=1\) 。
考虑 \(f[x]\) 的前几项。 \(f[x_1]=1,f[x_1+2]=1,f[x_1+4]=2,f[x_1+6]=4,f[x_1+8]=8...\) 。于是我们很高兴地发现 \(f[x]=2^{(x-x_1)/2-1}\),然后打一个快速幂就行。
\(code:\)
#include<iostream>
#include<cstdio>
using namespace std;
const long long mod=100000007;
long long t,n,m,ans;
long long f(long long x,long long y){
long long s=x;x=1;
while(y){
if(y&1)
x=x*s%mod;
s=s*s%mod;y>>=1;
}
return x;
}
int main(){
freopen("gta.in","r",stdin);
freopen("gta.out","w",stdout);
scanf("%lld",&t);
while(t--){
scanf("%lld%lld",&n,&m);
if((m-n)&1)
printf("0\n");
else if(m==n)
printf("1\n");
else{
printf("%lld\n",f(2,(m-n)/2-1));
}
}
fclose(stdin);fclose(stdout);
return 0;
}