前言

由于网络流极其庞大而资料有限，我决定用这个博客先记录一下我学习的大纲，在后期有可能补上内容。对于网上可以找到的，我就一笔带过，只是说明应该了解这个东西；而对于网上难以找到的一些资料，我会尽我所能写出来。

大纲

基本概念

网络最大流 - 增广路类

• 最大流最小割定理：内容与证明
• Ford - Fulkerson 增广：以下所有算法的基础，从贪心上简单地 支持反悔 的实现（增加反边容量）
• Edmonds - Karp（\(O(nm^2)\)）：从 F-F 到 EK 的优化，最短路不减 引理（BFS 寻找最短增广路）
• dinic（\(O(n^2 m)\)）：当前弧优化，整体 增广过程 的把握（多路增广）
• ISAP：单次 BFS 与 GAP（尤其是实现时 if(!ans) return flow; 阻止优化后的 dep 修改机制影响正确性）
• F-F \(\to\) EK \(\to\) dinic \(\to\) ISAP，其实是一个不断迭代优化的过程，贪心反悔贯穿始终。
• 时间复杂度证明：反证法 和 极限思想 的极致体现

dinic 复杂度证明（名字自己起的，内容自己证的，建议作为 OI-wiki 食用辅料）

• 单次多路增广上界：\(O(nm)\)

• 层次图层次严格单增证明：

  1. 合法延续性：原图或前代层次图的 高度标号 / 层次 在 多次迭代 后仍然 合法
     合法：任意两点的高度标号 / 层次 大小关系不变；
  2. 同长同层性：长度相同 的增广路的 对应节点 的 层次相同;
     \(\implies\) 这两条增广路在 同一层次图 上；
  3. 单次消失性：对 同一层次图 的任意增广路，必然有一条在增广路中的边在下一代残量网络中消失。

  故可证，每次迭代后的层次图严格单调递增。

关于 ISAP 你需要的

OI-wiki 的代码好像有问题，此外他本身也比较复杂，可以考虑使用如下代码。

\(\text{AC Code by ISAP with the current arc, gap and dep optimization, } 47 ms\text{ with O2.}\)

#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=205,M=5005;
int n,m,s,t;
struct flow_network {
	int cnt=1,head[N],to[M<<1],next[M<<1],lim[M<<1];
	int dep[N],gap[N];
	inline void add(int u,int v,int w) {
		to[++cnt]=v,lim[cnt]=w,next[cnt]=head[u],head[u]=cnt;
		to[++cnt]=u,lim[cnt]=0,next[cnt]=head[v],head[v]=cnt;
	}
	int cur[N];
	ll dfs(int u,ll ans) {
		if(u==t) return ans;
		ll flow=0;
		for(int &p=cur[u];p&&ans;p=next[p]) {
			int c=std::min(ans,(ll)lim[p]),v=to[p];
			if(dep[v]==dep[u]-1&&c) { int fl=dfs(v,c); flow+=fl,ans-=fl,lim[p^1]+=fl,lim[p]-=fl; }
			if(!ans) return flow;
		}
		if(--gap[dep[u]]==0) dep[s]=n;
		++gap[++dep[u]];
		return flow;
	}
	inline ll max_flow(int s,int t) {
		ll flow=0; std::queue<int> q;
		memset(dep,-1,sizeof dep);
		q.push(t),gap[dep[t]=0]=1;
		while(!q.empty()) {
			int u=q.front(); q.pop();
			forE(u) if(!lim[p] && dep[v]==-1) ++gap[dep[v]=dep[u]+1],q.push(v);
		}
		while(dep[s]<n) { memcpy(cur,head,sizeof head); flow+=dfs(s,1e18); }
		return flow;
	}
} f_n;
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m>>s>>t;
	for(int i=1,u,v,w;i<=m;++i) { std::cin>>u>>v>>w; f_n.add(u,v,w); }
	std::cout<<f_n.max_flow(s,t)<<'\n';
	return 0;
}

优化后的 ISAP 深度维护机制正确性证明

考虑采用数学归纳法。首先，我们先了解该机制的运行细节。

引理 1.　在多路增广中，增广路中满流的边靠近源点一侧的节点 \(u\) 到源点 \(T\) 的路径上的所有节点深度不改变。

考虑我们多路增广的过程 ll dfs(int u,ll ans)，dfs 的第二个传参 ans 表示阻塞流大小。所以从 \(u\) 到 \(T\) 的路径的 \(ans\) 必然被流光，即 \(ans=0.\) 根据 if(!ans) return flow; 必然直接返回，不改变深度。该引理得证。

接下来，我们分情况证明其正确性。

结论 2.　对于再无法提供贡献的节点，深度增加与深度赋值极大值等效。

考虑为无法贡献节点赋值极大值（一般是 \(n\)）的目的：使其无法再遍历。深度增加会使这些节点组成路径最终与汇点无法通过判断语句 dep[v]==dep[u]-1，进行联结，故深度增加与深度赋值极大值等效，该结论得证。但要注意的是，这种写法会导致这些节点在接下来的遍历过程中仍然被访问，（但无法抵达 \(T\)，没有贡献。）会增加一些复杂度，但整体影响不大。该深度维护机制在整体上对代码书写与运行速度的提升都是正向的。

结论 3.　对于还能继续产生贡献的节点，深度增加可以保证其所有边的贡献全部被计入。

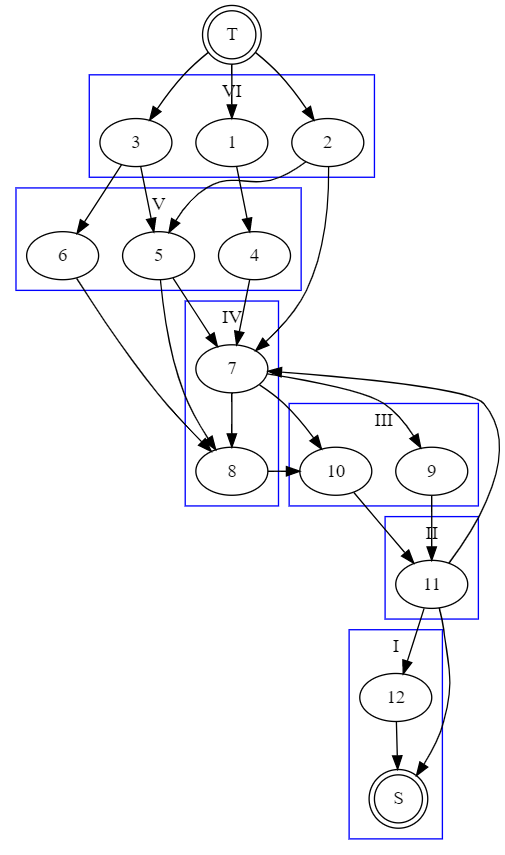
我们以汇点 \(T\) 为中心建立层次图，\(dis(u)\) 表示节点 \(u\) 的层次，将所有边大致分为以下几类：（名称是根据增广时的上下关系，自己取的。）

• 上溯边：前往 \(dis(u)<=dis(v)\) 的节点 \(v\) 的边，如 \((11,7),(7,8)\)；（即 \(u\) 更靠近 \(T\) 一侧）
• 合法边：前往 \(dis(u)=dis(v)+1\) 的节点 \(v\) 的边，如 \((7,9)\)；（当前层次图要走的边）
• 下越边：前往 \(dis(u)>dis(v)+1\) 的节点 \(v\) 的边，如 \((2,7)\)。（即 \(v\) 更靠近 \(T\) 一侧，但是 \(u,v\) 跨度不止一层）

接下来我们分别证明这些边的贡献会被计入。

• 上溯边：我们把所有上溯边抽象成如下模型：

  

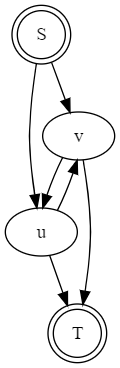
  其中 \((u,v)\) 是上溯边。

  考虑增广后在残量网络中消失的边的所有位置，会对该上溯边如下结果：

  • 边消失后，可达性不变或 \(v\) 不可达 \(u\)：对该上溯边无影响；
  • 边消失后，\(S\) 不可达 \(v\)：除经过该上溯边外，无法遍历至 \(v,\ v\) 深度不变。
  • 边消失后，\(S\) 不可达 \(u\) 或 \(v\) 不可达 \(T\)：该上溯边 不可能 再提供贡献。
  • 边消失后，\(u\) 不可达 \(T\)：\(u\) 成为 死胡同，根据引理 1，\(u\) 的深度将逐渐增加。

  至此易得，要么该上溯边 不可能 再提供贡献，要么在 \(S\) 不可达 \(v,\ u\) 不可达 \(T\) 后，\(v\) 深度不变，\(u\) 深度逐渐增加，必然有 \(dis(u)=dis(v)+1,\) 成为合法边。

• 合法边：若此次阻塞流不在边 \((u,v)\) 上，则 \(u,v\) 的深度同时增加，该边仍然合法，有机会在后续的遍历中继续被增广。

• 下越边：考虑下越边的定义，\(dis(u)\) 必然曾经定义为 \(dis(v)+1,\) 后因为该边 满流 等原因导致 \(u\) 深度增加而 \(v\) 深度不变。故该边若有贡献，必然在此代层次图前已经被计入。

综上，所有类型边的贡献均被计入，该结论得证。

根据结论 2 和结论 3，当前深度维护机制的正确性得以证明。

网络最大流 - 预留推进类

准备鸽了……OI中用处不大，学完其他的再学 qwq

无负环费用流

• 基于 EK 的 SSP：如何 结合 EK 和 SPFA，正确性证明
• 基于 dinic 的 SSP：如何 写出正确的代码，注意 dfs 错误可能导致 爆栈空间

魏老师没有给出 dinic 的 SSP 代码，这里我给一个我的版本：

\(\text{AC Code by SSP based on dinic with the current arc optimization, } 1.29s \text{ without O2.}\)

#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=5e3+3,M=5e4+4;
struct network {
	int cnt=1,head[N],to[M<<1],next[M<<1],lim[M<<1],cst[M<<1];
	inline void add(int u,int v,int w,int c) {
		to[++cnt]=v,lim[cnt]=w,cst[cnt]=c,next[cnt]=head[u],head[u]=cnt;
		to[++cnt]=u,lim[cnt]=0,cst[cnt]=-c,next[cnt]=head[v],head[v]=cnt;
	}
	int t,cost=0,cur[N],dis[N],in[N];
	int dfs(int u,int res) {
		if(u==t) return res;
		int flow=0; in[u]=1;
		for(int p=cur[u];p&&res;p=next[p]) {
			cur[u]=p;
			int c=std::min(lim[p],res),v=to[p];
			if(dis[u]+cst[p]==dis[v]&&c&&!in[v]) { int fl=dfs(v,c); flow+=fl,res-=fl,cost+=cst[p]*fl,lim[p]-=fl,lim[p^1]+=fl; }
		}
		if(!flow) dis[u]=-1;
		return in[u]=0,flow;
	}
	std::pair<int,int> mincost(int s,int t) {
		int flow=0; this->t=t;
		while(1) {
			std::queue<int> q;
			memcpy(cur,head,sizeof head);
			memset(dis,0x3f,sizeof dis);
			dis[s]=0,in[s]=1,q.push(s);
			while(!q.empty()) {
				int u=q.front(); in[u]=0,q.pop();
				forE(u) if(lim[p]&&dis[v]>dis[u]+cst[p]) {
					dis[v]=dis[u]+cst[p];
					if(!in[v]) in[v]=1,q.push(v);
				}
			}
			if(dis[t]>1e9) return {flow,cost};
			flow+=dfs(s,1e9);
		}
	}
} ntw;
int n,m,s,t;
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m>>s>>t;
	for(int i=1,u,v,w,c;i<=m;++i) { std::cin>>u>>v>>w>>c; ntw.add(u,v,w,c); }
	auto ret=ntw.mincost(s,t);
	std::cout<<ret.first<<' '<<ret.second<<'\n';
	return 0;
}