Acwing 4440 照相

laniser / 2023-06-14 / 原文

Acwing 4440 照相

原题指路

因为序列长为偶数，考虑将牛进行两两分组

为什么要将其进行两两分组:因为题目按偶数前缀进行反转，每一组中的牛总是相邻的，不会被拆散。

两两分组后会有四种情况: GG HH GH HG

我们再观察可得:每次反转，就是将每组内的两头牛进行互换

如:

而GG HH 反转并无影响

我们不妨将GH 定义为0(H在偶数位) HG 定义为1(G在偶数位) ,另外两种情况无影响直接舍去。

则对上述字符串可转化为一个01串:110 ,其反转规则如下:

题目要求求当G在偶数为的最大值时，需要反转的最小次数。因为要求G在偶数的最大值，即求变换多少次可将01串变为尽可能多的1的变换次数的最小。

我们不难发现任意一个01串都可以变为全0或全1，现给予如下举例证明:

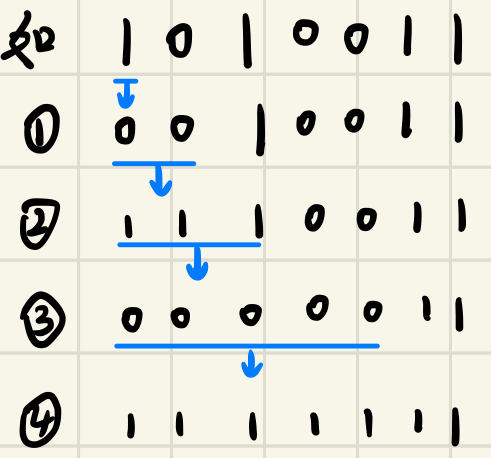
任意一个01串按上述方法变换都能变为全为1的串

我们就找到了G在偶数的最大值的可行解，现继续寻找最优解.

贪心找最优解：

若对任意01串.....01... 在1的后面进行反转我们无法将01全变为11,只能将串变为..10...... ,所以由此，我们可以得到启发，在每个0和1中间做一次反转

可以得到最小值(从前往后做这样的反转)

边界判断：当01串最后一位为0时，我们需要额外添加一步让其变为1。

具体代码：

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N=2e5+10;

int n,m;
char s[N];
int w[N];

int main(void)
{
    int res=0;
    cin>>n>>s;
    for(int i=0;i<n;i+=2)
        if(s[i]!=s[i+1])
            w[m++]=s[i]=='H';
    
    if(!w[m-1]) res++;
    for(int i=0;i<m-1;i++)
        if(w[i]!=w[i+1])
            res++;
            
    cout<<res<<endl;
    
    return 0;
}