treap树
Treap树 = tree+heap
数和堆的集合,每个节点有值val,也有优先级key,那么这棵树的形态就被确定了,和插入顺序无关了(有赖于优先级
避免退化成链:再生成节点时,随机生成优先级,然后插入时动态调整
1、FHQ treap又称无旋treap,没有旋转操作,使用分裂和合并两个操作维护树的平衡
struct node{
int l,r;
int val;
int key;
int size;
}tr[N];
int root,idx;
int newnode(int v){
}
void pushup(){ //向上更新
}
void split(int p,int v,int &x,int &y){ //分裂操作 注意在递归的过程中,连接了分裂后的新边
}
int merg(int x,int y){ //合并,根据key的大小,注意在递归的过程中,连接了分裂后的新边
}
void inser(int v){ //插入节点,先分裂,再合并,连续两次合并
}
void del(int v){ //删除操作,先分裂、再合并
}
int get_k(int p,int k){ //返回第k个节点
}
void get_pre(int v){ //找前驱
}
void get_suc(int v){ //找后继
}
void get_rank(int v){//排名
}
void get_val(int k){//数值
}
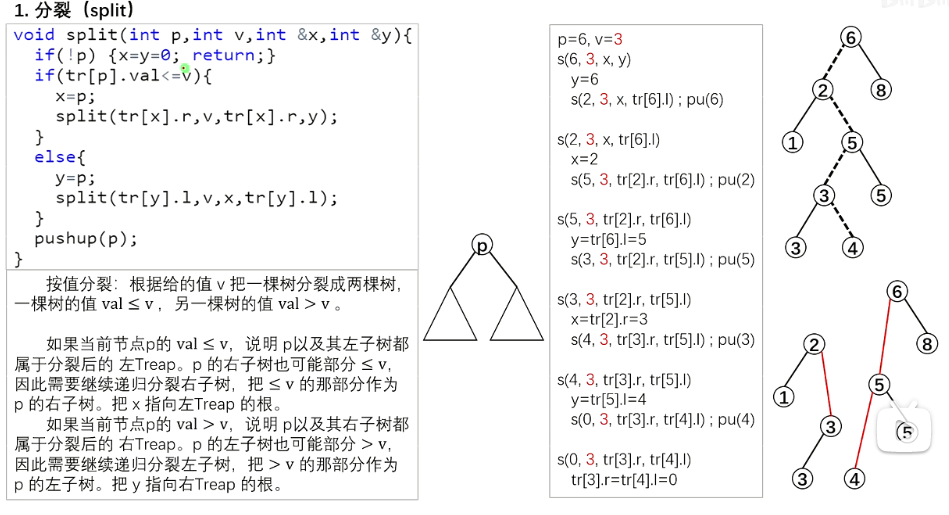
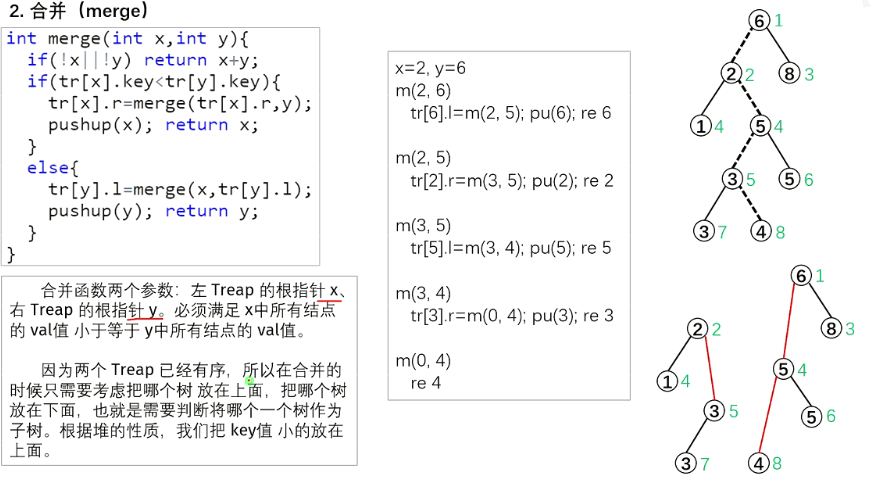
删除:如果有两个子节点,找到优先级大的,把x向反方向旋转,也就是把x向树的下层调整,直到旋转到叶子节点
!很多题目涉及名次树
常用操作:
struct node,旋转rotate,插入insert(),查找第k大的数kth(),查询某个数find()【名次树】
少林 hdu 4585
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll inf = 4e18+10;
const int mod = 1000000007;
const int mx = 5e6+5; //check the limits, dummy
typedef pair<int, int> pa;
const double PI = acos(-1);
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
#define swa(a,b) a^=b^=a^=b
#define re(i,a,b) for(int i=(a),_=(b);i<_;i++)
#define rb(i,a,b) for(int i=(b),_=(a);i>=_;i--)
#define clr(a) memset(a, 0, sizeof(a))
#define lowbit(x) ((x)&(x-1))
#define mkp make_pair
void sc(int& x) { scanf("%d", &x); }void sc(int64_t& x) { scanf("%lld", &x); }void sc(double& x) { scanf("%lf", &x); }void sc(char& x) { scanf(" %c", &x); }void sc(char* x) { scanf("%s", x); }
int m, n,k,sum=0,ans=0,t;
int id[mx];
struct node
{
int size;//以这个节点为根的子树的节点总数,用于名次树
int rank;//优先级
int key;//键值
node *son[2];//son[0]左儿子,son[1]右儿子
bool operator<(const node& a)const { return rank < a.rank;}
int cmp(int x)const {
if (x == key)return -1;
return x < key ? 0 : 1;
}
void update() {
size = 1;
if (son[0] != NULL)size += son[0]->size;
if (son[1] != NULL)size += son[1]->size;
}
};
void rotate(node* &o, int d) {//d=0,左旋,d=1,右旋
node *k = o->son[d ^ 1];//d^1等价于1-d,但是更快
o->son[d ^ 1] = k->son[d];
k->son[d] = o;
o->update();
k->update();
o = k;
}
void insert(node* &o, int x) {//把x插入树中
if (o == NULL) {
o = new node();
o->son[0] = o->son[1] = NULL;
o->rank = rand();
o->key = x;
o->size = 1;
}
else {
int d = o->cmp(x);
insert(o->son[d],x);
o->update();
if (o < o->son[d]);
rotate(o, d ^ 1);
}
}
int kth(node* o, int k) {//返回第k大的数
if (o == NULL || k <= 0 || k > o->size)
return -1;
int s = o->son[1] == NULL ? 0 : o->son[1]->size;
if (k == s + 1)return o->key;
else if (k <= s)return kth(o->son[1], k);
else return kth(o->son[0], k - s - 1);
}
int find(node* o, int k) {//返回元素k的名次
if (o == NULL)
return -1;
int d = o->cmp(k);
if (d == -1)
return o->son[1] == NULL ? 1 : o->son[1]->size + 1;
else if (d == 1)return find(o->son[d],k);
else {
int tmp = find(o->son[d], k);
if (tmp == -1)
return -1;
else {
return o->son[1] == NULL ? tmp + 1 : tmp + 1 + o ->son[1]->size;
}
}
}
int main()
{
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
while (cin>>n&&n)
{
srand(time(NULL));
int k, g;
cin >> k >> g;
node* root = new node();
root->son[0] = root-> son[1] = NULL;
root->rank = rand();
root->key = g;
root->size = 1;
id[g] = k;
cout << k << ' ' << 1<<endl;
re(i, 2, n + 1) {
cin >> k >> g;
id[g] = k;
insert(root, g);
t = find(root, g);//返回新和尚的名次
int ans1, ans2;
ans1 = kth(root, t - 1);//前一名的老和尚
ans2 = kth(root, t + 1);//后一名的老和尚
if (ans1 != -1 && ans2 != -1)
{
ans = ans1 - g >= g - ans2 ? ans2 : ans1;
}
else if (ans1 == -1)
ans = ans2;
else ans = ans1;
cout << k << ' ' << id[ans] << endl;
}
}
return 0;
}