[题目记录]一本通高手训练-数列

youlv / 2024-10-12 / 原文

题意

定义 n-数列为满足以下条件的数列 ${a_i}$ :

数列长度不小于 $3$ , 且每个元素为 $1$ 到 $n$ 的整数 .
对于任意 $k \ge 3$ , 有 $ (a_k-a_{k-2})(a_{k-1}-a_{k-2})<0$ .

给出 $n$ , 求 n-数列的个数 , 对 $10^9+7$ 取模 .

$n\le 10^{500000}$

时空限制 $1s,512MB$

题解

第二个条件的易于理解的说法是 : 每个元素的大小都介于后两个元素之间 . 而对于每个限制 , 都有两种情况 , 即 $a_k>a_{k-2}>a_{k-1} $ 或 $a_k<a_{k-2}<a_{k-1} $ .

尝试手动模拟大小关系 , 发现这些大小关系的限制很紧 , 如图 :

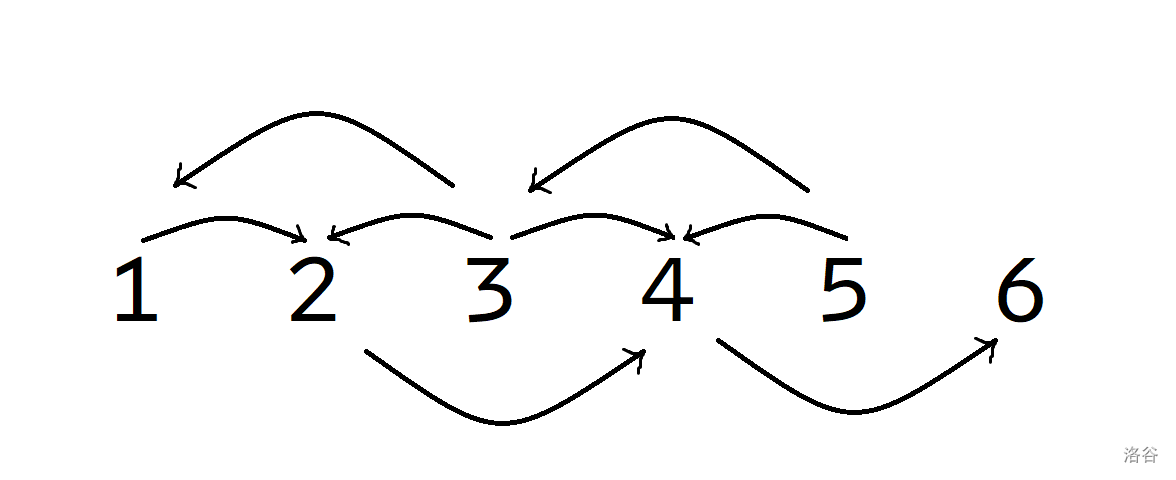
逐个条件进行推导 , 当我们钦定 $a_2<a_3$ , 就一定有 $ a_3>a_4$ , $ a_4 <a_5$ 等等 . 也就是说 , 一旦 $a_2,a_3$ 的大小关系得以确定 , 所有的限制都只剩下一种情况 .

而观察 $a_2<a_3$ 情况下的所有大小关系 , 发现这些关系中包含一个完整的链 : $ 5>4>1>2>4 $ . $a_2 > a_3$ 同理 .

因此对于确定的 $k$ 个不同数字 , 组成一个合法序列的方法有且仅有 $2$ 种.

对于一个长度为 $k$ 的 n-数列 , 相当于在 $n$ 个数字里选互不相同的 $k$ 个 , 每种选择方案对应两个序列 . 可得答案即为 :

\[2\times\sum_{k=3}^{n} C_n^k\\ =2\times(\sum_{k=1}^{n} C_n^k - C_n^0- C_n^1- C_n^2) \\ =2\times(2^n-1-n-\frac{n(n-1)}{2}) \]

最后 , 因为要取模 , 所以高精度是没有必要的 . 分别逐位读取处理 $n\mod p $ 与 $2^n \mod p $ 即可 .

代码

#include<bits/stdc++.h>
#define file(x) freopen(#x ".in","r",stdin),freopen(#x ".out","w",stdout)
#define int long long
#define INF 0x3f3f3f3f
#define INF64 1e18
using namespace std;

constexpr int N=26;
constexpr int p=1e9+7;

int qp(int x,int t){
	int res=1;
	while(t){
		if(t&1) res=res*x%p;
		x=x*x%p;
		t>>=1;
	}
	return res;
}

string s;

signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>s;
	int x=0,y=1;
	for(int i=0;i<s.length();i++) x=(x*10+s[i]-'0')%p,y=qp(y,10)*qp(2,s[i]-'0')%p;
	cout<<2*(y-1-x-x*(x-1)/2%p+2*p)%p;
}