最长子序列
例题
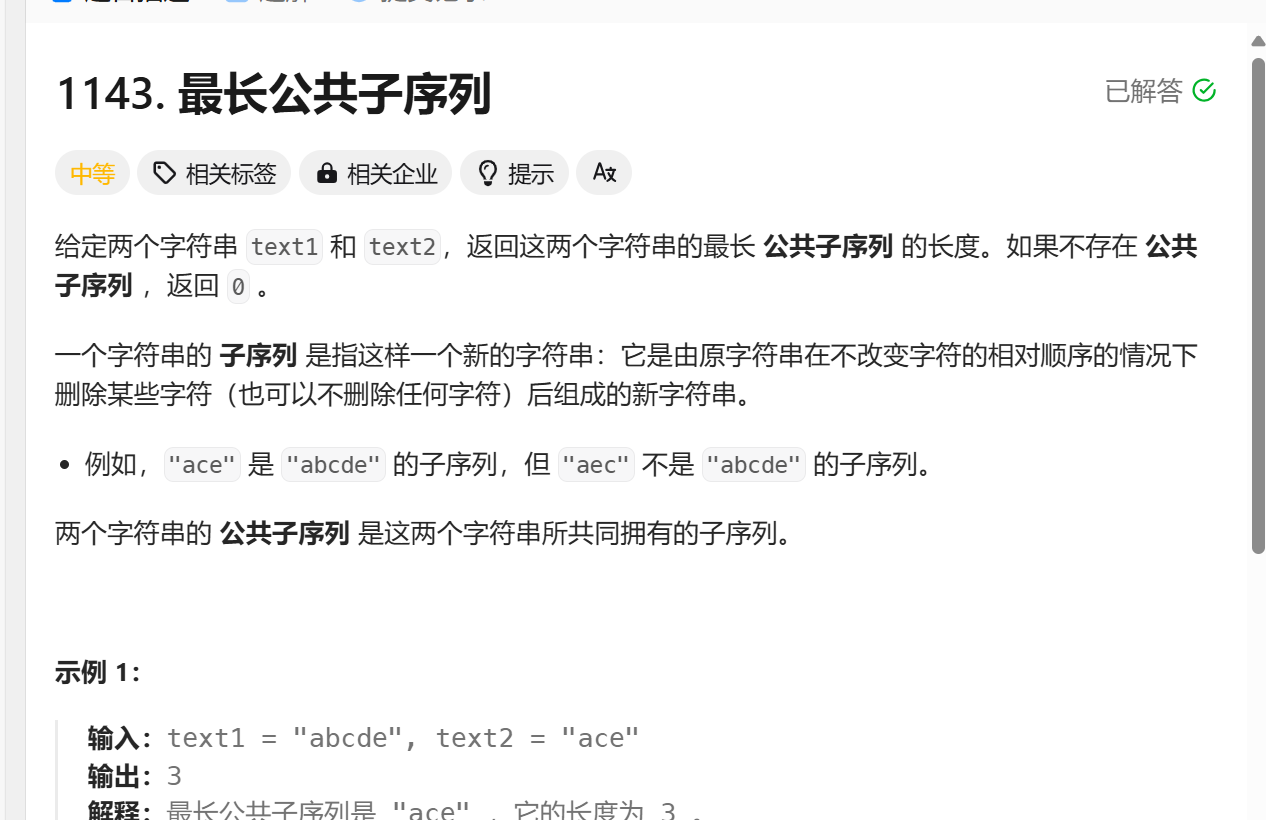
两个字符串的最长公共子序列其实可以理解为一个二维dp
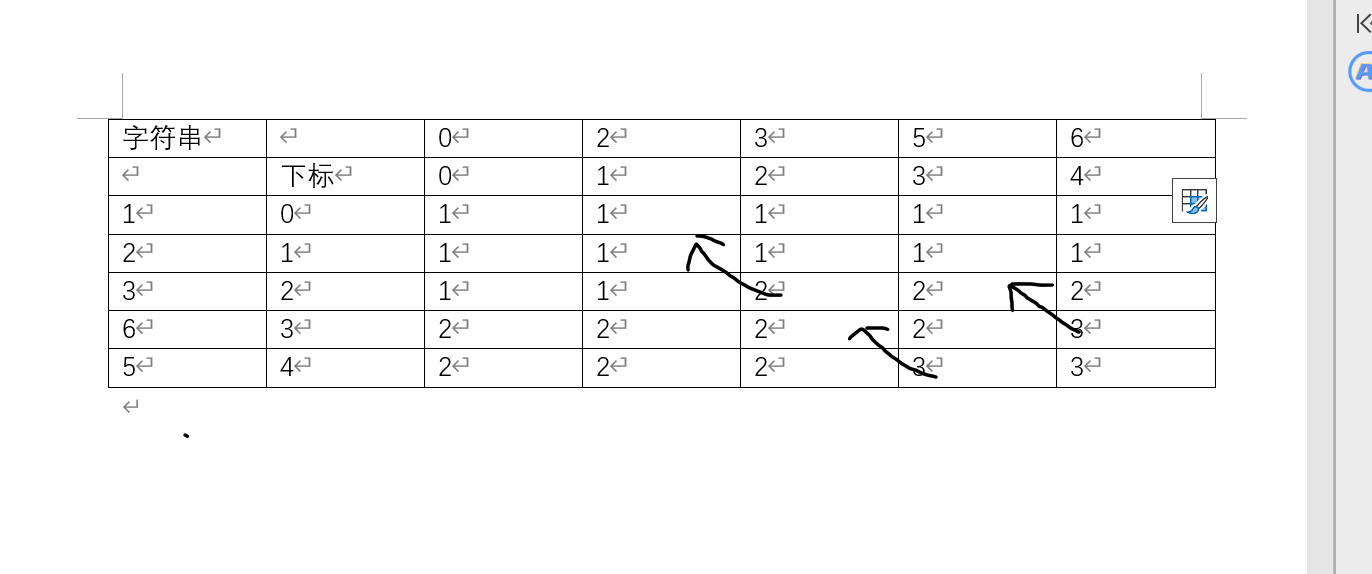
如图,每个格子都代表的是当以当前下标为结尾的时候所能构成的最长序列,每个格子都有三种转移方式,不要a的末尾,不要b的末尾和两个都不要,当a[i]b[j]的时候,此时,a[i]b[j],就是从箭头所指的方位转移了过来,也就是两个字符串的结尾都不要,相当于直接从dp[i-1][j-1]的情况加了1,这也是下面为什么max()只需要比dp[i-1][j]和dp[i][j-1]。因此,我们就能得出当a[i]b[j]的情况代码,dp[i][j]=dp[i-1][j-1]+1;而当不相等时,则要选取其中一种情况,要么不要a的末尾,要么不要b的末尾,我们由此便可得出dp[i][j]=max(dp[i-1][j],dp[i][j-1]);此外,我们还要算个数,方案数其实就如同上面的情况一般,不同的是,因为dp[i-1][j]和dp[i][j-1]都是经过了dp[i-1],[j-1]转移过来,所以当a[i]!=b[j]&&dp[i][j]dp[i-1][j-1],dp[i][j]多加了一次dp[i-1][j-1]。
所以,代码如下
点击查看代码
#include <iostream> // 输入输出流
#include <iomanip> // 输入输出格式控制
#include <fstream> // 文件输入输出流
#include <sstream> // 字符串输入输出流
#include <cmath> // 数学函数
#include <string> // 字符串操作
#include <vector> // 动态数组容器
#include <queue> // 队列容器
#include <stack> // 栈容器
#include <set> // 集合容器
#include <map> // 映射容器
#include <unordered_set> // 无序集合容器
#include <unordered_map> // 无序映射容器
#include <algorithm> // 算法
#include <bitset> // 位集容器
#include <stdio.h> // 标准输入输出
using namespace std;
typedef long long ll;
int dp[1001][1001];
ll cnt[1001][1001];
const int mod = 100000000;
string a, b;
void print(int n, int m)
{
if (n == 0 || m == 0)
return;
if (dp[n][m] == dp[n - 1][m - 1] + 1)
{
print(n - 1, m - 1);
cout << a[n];
}
else if (dp[n][m] == dp[n - 1][m])
print(n - 1, m);
else
print(n, m - 1);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cout << fixed << setprecision(12);
cin >> a >> b;
int n = a.size(), m = b.size();
a = " " + a;
b = " " + b;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
if (a[i] == b[j])
{
dp[i][j] = dp[i - 1][j - 1] + 1;
}
else
{
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
cout << dp[n][m]<< endl;
// // 个数
for (int i = 0; i <= m; i++)
{
cnt[0][i] = 1;
}
for (int i = 0; i <= n; i++)
{
cnt[i][0] = 1;
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
ll u = cnt[i][j];
if (a[i] == b[j] && dp[i][j] == dp[i - 1][j - 1] + 1)
u = (u + cnt[i - 1][j - 1]) % mod;
if (dp[i][j] == dp[i - 1][j])
u = (u + cnt[i - 1][j]) % mod;
if (dp[i][j] == dp[i][j - 1])
u = (u + cnt[i][j - 1]) % mod;
if (a[i] != b[j] && dp[i][j] == dp[i - 1][j - 1])
u = ((u - cnt[i - 1][j - 1]) % mod + mod) % mod;
cnt[i][j] = u;
}
}
cout << cnt[n][m] << endl;
// 最长字串
// print(n, m);
return 0;
}
这个代码也有很大的限制,在空间上有很大限制,所以可以用滚动数组来优化一下
点击查看代码
#include <iostream> // 输入输出流
#include <iomanip> // 输入输出格式控制
#include <fstream> // 文件输入输出流
#include <sstream> // 字符串输入输出流
#include <cmath> // 数学函数
#include <string> // 字符串操作
#include <vector> // 动态数组容器
#include <queue> // 队列容器
#include <stack> // 栈容器
#include <set> // 集合容器
#include <map> // 映射容器
#include <unordered_set> // 无序集合容器
#include <unordered_map> // 无序映射容器
#include <algorithm> // 算法
#include <bitset> // 位集容器
#include <stdio.h> // 标准输入输出
using namespace std;
typedef long long ll;
int dp[2][10001];
ll cnt[2][10001];
const int mod = 100000000;
string a, b;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cout << fixed << setprecision(12);
cin >> a >> b;
int n = a.size(), m = b.size();
a = " " + a;
b = " " + b;
for (int i = 0; i <= m; i++)
{
cnt[0][i] = 1;
}
cnt[1][0] = 1;
for (int i = 1; i <= n; i++)
{
int now = i & 1, pre = now ^ 1;//&和^的结果是反过来的,所以pre就可以代表上一次的状态
for (int j = 1; j <= m; j++)
{
dp[now][j] = max(dp[pre][j], dp[now][j - 1]);
if (a[i] == b[j])
{
dp[now][j] = max(dp[now][j], dp[pre][j - 1] + 1);
}
cnt[now][j] = 0;//滚动到当前的状态,cnt清零防止被上次的影响
if (a[i] == b[j] && dp[now][j] == dp[pre][j - 1] + 1)
{
cnt[now][j] = (cnt[now][j] + cnt[pre][j - 1]) % mod;
}
if (dp[now][j] == dp[pre][j])
{
cnt[now][j] = (cnt[now][j] + cnt[pre][j]) % mod;
}
if (dp[now][j] == dp[now][j - 1])
{
cnt[now][j] = (cnt[now][j] + cnt[now][j - 1]) % mod;
}
if (a[i] != b[j] && dp[now][j] == dp[pre][j - 1])//此时的dp[now][j]被dp[pre][j-1]影响了两次。
{
cnt[now][j] = ((cnt[now][j] - cnt[pre][j - 1]) + mod) % mod;
}
}
}
cout << dp[n & 1][m] - 1 << endl;
cout << cnt[n & 1][m] << endl;
return 0;
}