2024CCPC山东邀请赛 IAFCK
2024CCPC山东邀请赛 IAFCK
I. Left Shifting
思路:要第一个和最后一个一样,那找到第一个连续的两个一样的就是答案。如果一开始第一个和最后一个就是一样的,那就是0。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int t; cin>>t;
while(t--)
{
string s; cin>>s;
int n = s.size();
s = "?"+s;
if(s[1] == s[n]){
cout<<"0\n";
continue;
}
bool ok = false;
for(int i = 1;i < n; i++){
if(s[i]==s[i+1]){
ok = true;
cout<<i<<"\n";
break;
}
}
if(!ok)cout<<"-1\n";
}
return 0;
}
A. Printer
思路:发现存在单调性,并且很好去check,直接上二分。
check部分:
先对于每一个机器,先算出一个运行周期是\(t\times l+w\)。然后对于二分的答案\(x\)时间看能生成多少?
先看它有多少个完整的运行周期,即\(x/(t\times l+w)\),完整的运行周期生产\(x/(t\times l+w)\times l\)。
再看第二部分剩余的时间\(rem = x-x/(t\times l + w)\times (t\times l+w)\)
如果\(rem > t\times l\)了那么\(rem\)不能全去做生成,并且也不够一个完整周期,所以这段时间生成的一定是\(l\)个。
否则的话,这段剩余时间生产的数量就是\(rem/t\)个。
最后两部分加起来,如果\(\ge k\)则满足条件。
要小心的是:注意这题可能写的时候会爆long long小心一点,或者直接开int128。还有就是注意二分上界是\(2e18\)(极限情况\(t = 1,l = 1e9,w =1e9,k = 1e9\),则至少要(\((1e9+1e9)\times 1e9 = 2e18\))。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e5 + 10;
struct ty
{
ll t,l,w;
}a[N];
ll n,k;
bool judge(ll x)
{
__int128 ans = 0;
for(int i = 1;i <= n; i++)
{
__int128 t = a[i].t,l = a[i].l,w = a[i].w;
__int128 res = x/(t*l+w)*l;
__int128 rem = x-x/(t*l+w)*(t*l+w);
if(rem > t*l)
res += l;
else
res += rem/t;
ans += res;
}
return ans >= k;
}
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int t; cin>>t;
while(t--)
{
cin>>n>>k;
for(int i = 1;i <= n; i++)
{
cin>>a[i].t>>a[i].l>>a[i].w;
}
__int128 l = 0,r = 2e18;
while(l <= r)
{
__int128 mid = (l+r)>>1;
if(judge(mid))r = mid-1;
else l = mid + 1;
}
cout<<(ll)r+1<<'\n';
}
return 0;
}
F. Divide the Sequence
思路:首先看到数据范围那么大,感觉是个结论的数学题或者找规律那种。然后开始推式子,对\(\sum_{i = 1}^ki\times s_i\)这个式子进行变换。
我们知道分成若干个区间:\([l_1,r_1],[l_2,r_2],...,[l_k,r_k]\)。
结合前缀和思想就是:\(\sum_{i = 1}^ki\times s_i=1\times(s[r_1]-s[l_1-1])+2\times(s[r_2]-s[l_2-1])+3\times(s[r_3]-s[l_3-1])+...+k\times(s[r_k]-s[l_k-1])\)
又因为这些区间都是连续的,进而可以化简为:\(\sum_{i = 1}^ki\times s_i=1\times(s[r_1]-s[0])+2\times(s[r_2]-s[r_1])+3\times(s[r_3]-s[r2])+...+k\times(s[r_k]-s[r_{k-1}])\)
展开化简得:\(\sum_{i = 1}^ki\times s_i=k\times s[n]-s[r_1]-s[r_2]-...-s[r_{k-1}]\)。
而\(s[n]\)是固定的,我们要结果越大,只需要减去的越小越好,我们找到前\(k-1\)个最小的前缀和即可。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 5e5 + 10;
ll a[N],s[N];
bool cmp(ll x,ll y)
{
return x > y;
}
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int t; cin>>t;
while(t--)
{
int n; cin>>n;
for(int i = 1;i <= n; i++)
cin>>a[i];
for(int i = 1;i <= n; i++)
s[i] = s[i-1]+a[i];
sort(s+1,s+n);
ll x = 0;
for(int i = 1;i <= n; i++){
cout<<i*s[n]-x<<' ';
x += s[i];
}
cout<<"\n";
}
return 0;
}
K. Matrix
思路:这题是个构造呀,藕最讨厌构造哩,想到就会,想不到就寄(。
因为对于\(1\)~\(2n\)要至少出现一次,并且所有四个角组成的矩形里面只能有一个四个角都不一样。
我们可以怎么构造呢?
以5为例,可以考虑先这样子把10个数字填完,并且此时已经有一个四个都不一样的了。现在我们要保证的是其他都存在至少2个一样。
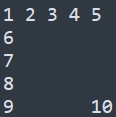
一开始我们想的是:直接填和左边一样的,然后发现:
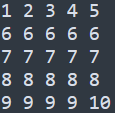
但是不对呀,最后一行和第一行组成的出现的四个都不同。怎么办呢?考虑最后一排特别。既然它和第一排不一样,那么我让它一样不就行啦,然后我们得到了:
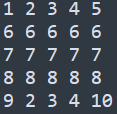
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9 + 7;
const int N = 2e3 + 10;
int a[N][N];
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int n; cin>>n;
if(n<=3)
{
cout<<"Yes\n";
if(n==2)
{
cout<<"1 2\n";
cout<<"3 4\n";
}
if(n==3)
{
cout<<"3 2 6\n";
cout<<"4 3 3\n";
cout<<"3 1 5\n";
}
}else{
cout<<"Yes\n";
int cnt = 0;
for(int i = 1;i <= n; i++)
a[1][i] = ++cnt;
for(int i = 2;i <= n; i++)
a[i][1] = ++cnt;
a[n][n] = ++cnt;
for(int i = 2;i <= n; i++)
for(int j = 2;j <= n; j++)
{
a[i][j] = a[i][j-1];
}
a[n][n] = cnt;
for(int i = 2;i < n; i++)
a[n][i] = a[1][i];
for(int i = 1;i <= n; i++){
for(int j = 1;j <= n; j++)
{
cout<<a[i][j]<<" ";
}
cout<<"\n";
}
}
return 0;
}
C. Colorful Segments 2
思路:区间覆盖+组合数学。
因为我们发现后面的贡献只会受到它前面的情况的约束,那么我们考虑先按左端点排序。之后呢,第一个的颜色情况肯定是\(k\),我们从第二个开始考虑,先默认是\(k-1\)。如果发现,当前的左端点比之前所有的右端点还要大了,说明没有覆盖了,并且那些右端点不会对后面有新的影响了,我们把k++,并且不要再管这个没有用的右端点了。
也就是说,当前的贡献,只需考虑前面的右端点。那么我们可以用一个小根堆去维护右端点。如果当前的左端点比之前出现的右端点大了,那么把这些不可能再产生影响的右端点pop掉,并且k++。下一次循环之前先k--(默认有覆盖,如果没有也是会加回来的,所以先减去,注意不要变成负数所以和0取个max)。每算完一个后把贡献依次乘起来就是答案啦(组合数学,分步乘法)。
// AC one more times
// nndbk
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 998244353;
const int N = 5e5 + 10;
struct ty
{
int l,r;
}a[N];
bool cmp(ty a,ty b)
{
return a.l < b.l;
}
int main()
{
ios::sync_with_stdio(false); cin.tie(nullptr), cout.tie(nullptr);
int t; cin>>t;
while(t--)
{
int n,k; cin>>n>>k;
for(int i = 1;i <= n; i++)
cin>>a[i].l>>a[i].r;
sort(a+1,a+1+n,cmp);
priority_queue<int,vector<int>,greater<int>>q;
q.push(a[1].r);
ll ans = k % mod;
k--;
for(int i = 2;i <= n; i++)
{
while(!q.empty() && q.top() < a[i].l){
k++;
q.pop();
}
ans = ans*k%mod;
k--;
k = max(0,k);
q.push(a[i].r);
}
cout<<ans<<"\n";
}
return 0;
}