差分

catting123 / 2023-05-20 / 原文

差分

前缀和的逆运算，能降低时间复杂度。

定义

给定原数组 \(a:a[1], a[2], ..., a[n]\)，构造数组 \(b: b[1], b[2], ..., b[n]\)，使得\(a[i]=b[1]+b[2]+...+b[i]\)。

\(a\) 数组是 \(b\) 数组的前缀和数组，\(b\) 数组是 \(a\) 数组的差分数组。

构造

构造 \(b\) 数组的方法：

\[b[i]=\left\{\begin{array}{ll} a[i]-a[i-1] & i \in[2, n]\\ a[1] & i=1 \end{array}\right. \]

可以在输入 \(a\) 数组的同时构造 \(b\) 数组，通过前缀和运算可以在 \(O(n)\) 时间内得到 \(b\) 数组。

用途

给数组 \(a\) 在区间 \([l, r]\) 中的的每一个数都加上常数 \(c\)，即 \(a[l]+c, a[l+1]+c, ..., a[r]+c\)。

可以直接遍历，从 \(l\) 循环到 \(r\) 区间，时间复杂度为 \(O(n)\)，如果循环 \(m\) 次，时间复杂度为 \(O(m\times n)\)，这时可以使用差分数组。

b[l] += c;
b[r+1] -= c;

仅需两句即可实现给给数组 \(a\) 在区间 \([l, r]\) 中的的每一个数都加上常数 \(c\)，时间复杂度为\(O(1)\)，如果循环 \(m\) 次，时间复杂度为 \(O(m)\)，大大降低了时间复杂度。

解释

因为 \(a[i]=b[1]+b[2]+...+b[i]\)，b[l] += c实现的是给a[l]及a[l]后面的数都加c，而b[r+1] -= c实现的是给a[r+1]及a[r+1]后面的数都减c，和前面加减相消，a[r+1]及a[r+1]后面的数大小不变。

实践

题目

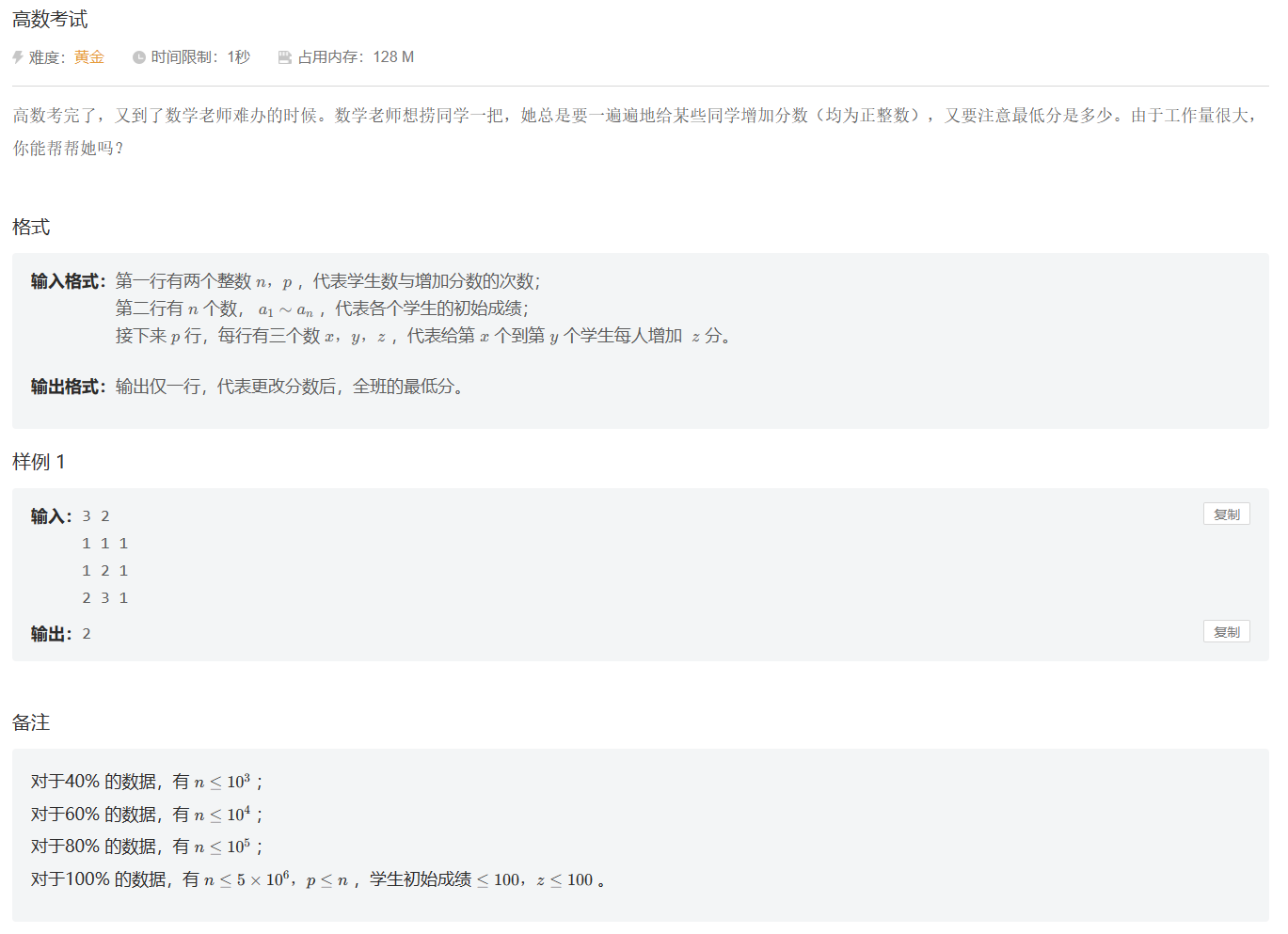
解答

#include<iostream>
using namespace std;
const int N = 1e7 + 5;
int n, p;
int a[N], b[N];
int ans = 0x3f3f3f3f;

int main() {
    scanf("%d%d", &n, &p);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        b[i] = a[i] - a[i - 1];
    }
    for (int i = 1; i <= p; i++) {
        int x, y, z;
        scanf("%d%d%d", &x, &y, &z);
        b[x] += z;
        b[y + 1] -= z;
    }
    for (int i = 1; i <= n; i++) {
        a[i] = a[i - 1] + b[i];
        ans = min(a[i], ans);
    }
    printf("%d", ans);
    return 0;
}