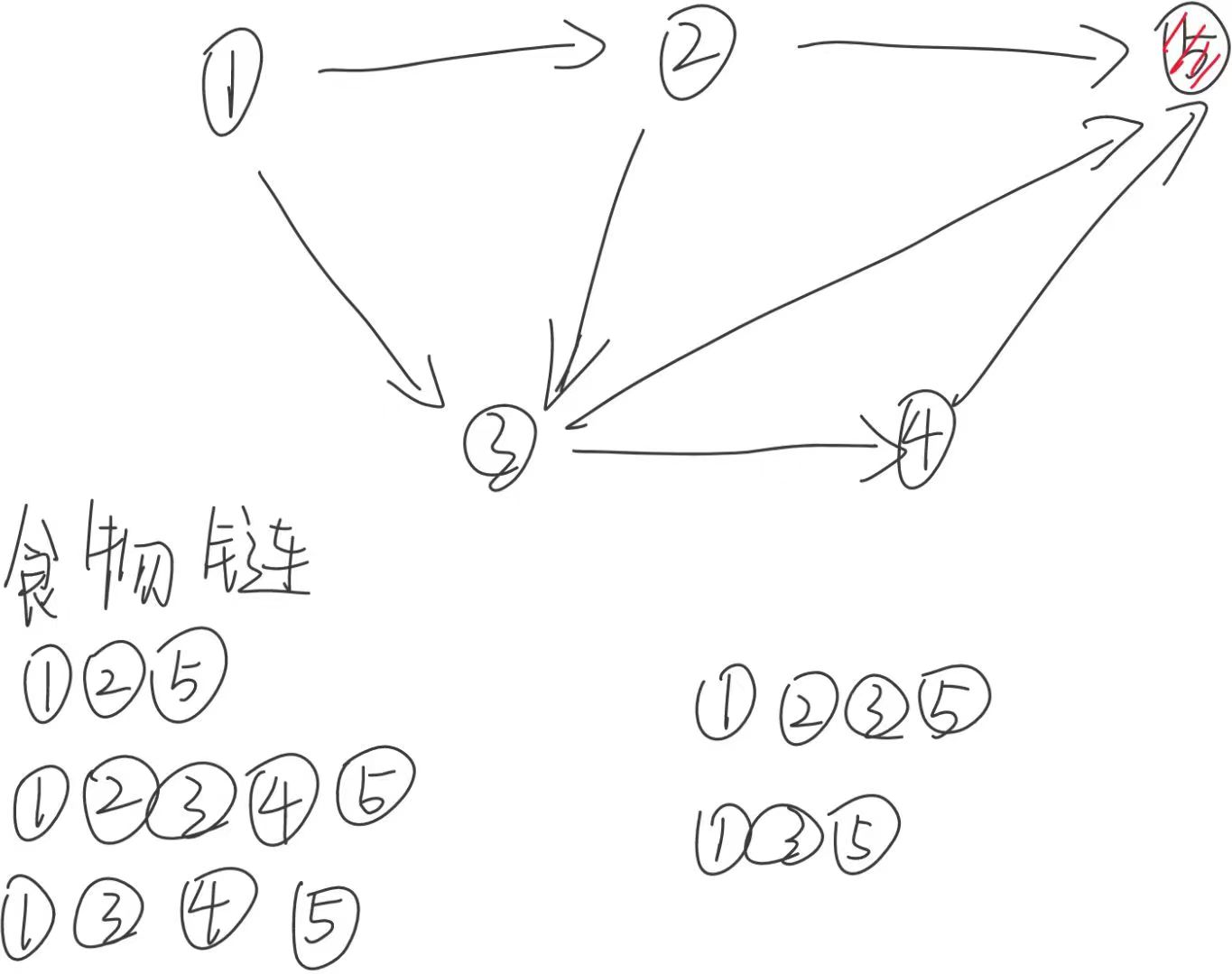
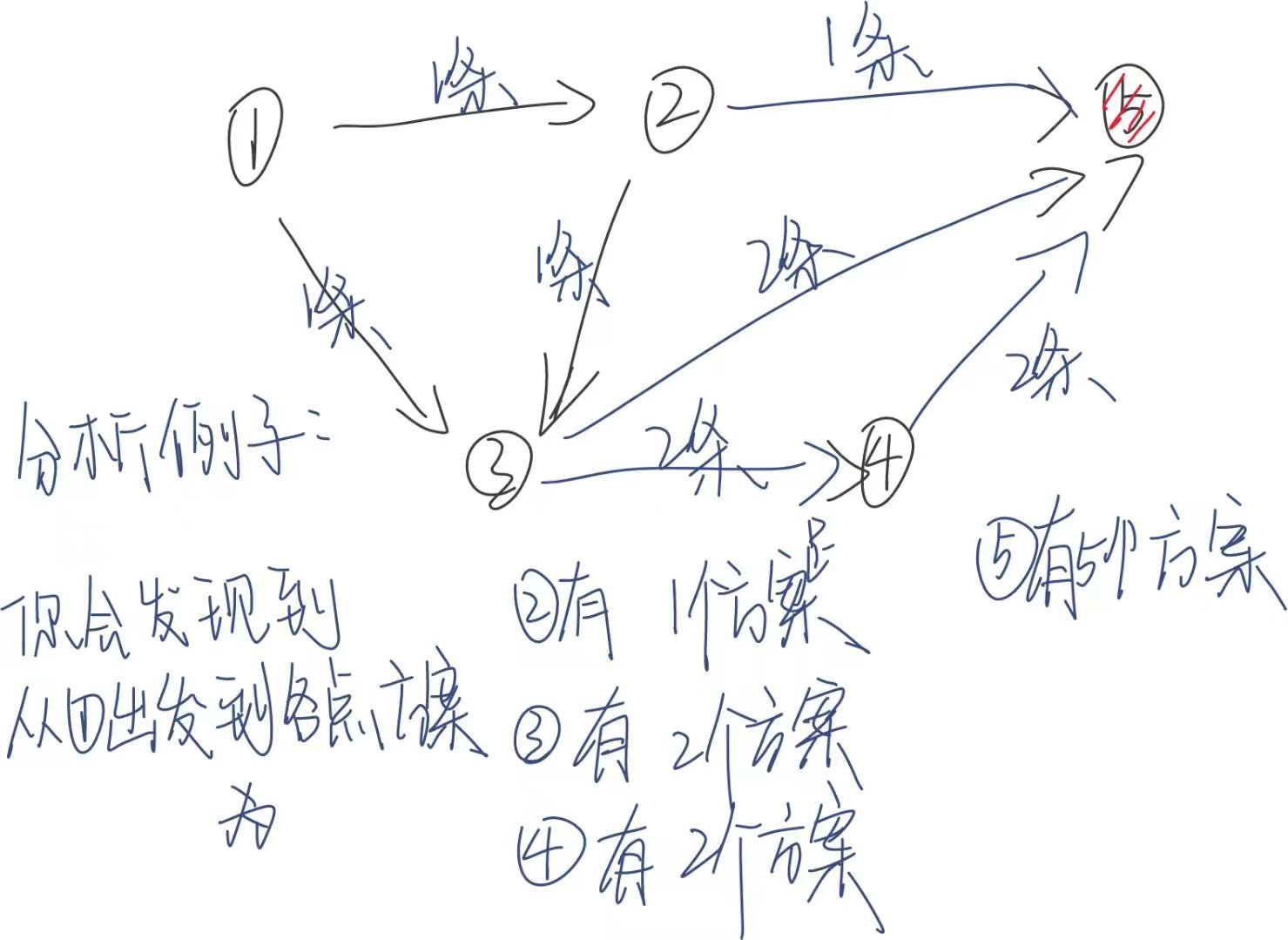
给你一个食物网,求出这个最大食物链的数量
最大食物链定义为左端不会捕食其他捕食者,最右端不会被捕食. 
解释看例子

第1行
n m 表示生物种类n 和 吃和被吃的关系m
接下来m行
A B 表示A被B吃
....

举个例子 
A -> B -> C -> D
A 是最左端的物种，它不会被其他物种捕食。
D 是最右端的物种，它不会捕食其他物种。
因此，食物链 A -> B -> C -> D 符合最大食物链的定义。

input:
5 7
1 2
1 3
2 3
3 5
2 5
4 5
3 4

output: 
5

在食物网中，拓扑排序可以帮助确定没有被其他物种捕食的起点物种。拓扑排序的起点是入度为零的顶点，即没有其他物种捕食它们的物种

通过反向拓扑排序（从入度为零的顶点开始逆向排序），可以确定没有捕食其他物种的终点物种。这些物种不会捕食其他物种，即它们的出度为零

一旦确定了起点和终点，从起点开始沿着拓扑排序的顺序向后遍历，直到到达终点为止，构成的路径即为一个最大食物链

因此，拓扑排序在最大食物链问题中的应用，主要是通过确定图中的入度和出度关系，帮助找到满足定义的起点和终点，进而构建出最大食物链

const int N = 5e3 + 5, M = 5e5 + 5, mod = 80112002;
int indep[N], head[N], dp[N], n, m, cnt = 1, ans;
struct Edge {
    int to, next;
} edges[M];
N, M 和 mod 是常量，分别表示节点数上限、边数上限和取模的数值。
indep[N]：数组，存储每个节点的入度。
head[N]：数组，存储每个节点的第一条出边的索引。
dp[N]：数组，用于动态规划，存储从起点到每个节点的路径数。
n 和 m：整数，表示节点数和边数。
cnt：整数，用于边数组的索引计数。
ans：整数，用于存储最终的结果，即最大食物链数量。


void init() {
    for (int i = 1; i < N; i++) {
        head[i] = -1;
    }
    for (int i = 1; i < M; i++) {
        edges[i].next = -1;
    }
}
init() 函数用于初始化 head[] 和 edges[] 数组。
将 head[] 数组的每个元素初始化为 -1，表示每个节点的出边链表为空。
将 edges[] 数组的 next 字段初始化为 -1，表示边数组的下一个指针为空。

void addedge(int from, int to) {
    edges[cnt] = {to, head[from]};
    head[from] = cnt++;
    indep[to]++;
}
addedge(from, to) 函数用于向图中添加一条从 from 到 to 的有向边。
将 to 添加到 from 的边链表中，更新 head[] 数组和 edges[] 数组。
同时更新 indep[] 数组，表示 to 的入度加一。

void Toposort() {
    queue<int> q;
    for (int i = 1; i <= n; ++i) {
        if (!indep[i]) {
            q.push(i);
            dp[i] = 1; // 起始点的 dp 值为1
        }
    }
    while (!q.empty()) {
        int from = q.front();
        q.pop();
        if (head[from] == -1) {
            ans = (ans + dp[from]) % mod;
        }
        for (int to = head[from]; ~to; to = edges[to].next) {
            dp[edges[to].to] = (dp[edges[to].to] + dp[from]) % mod;
            if (--indep[edges[to].to] == 0) {
                q.push(edges[to].to);
            }
        }
    }
    cout << ans;
}
Toposort() 函数实现了拓扑排序，计算最大食物链的数量。
使用队列 q 存储入度为0的节点，并初始化其 dp[] 值为1。
遍历队列中的节点 from，处理其出边：
更新相邻节点 to 的 dp[] 值，表示从 from 到 to 的路径数。
如果 to 的入度减为0，将其加入队列 q 中。
当遍历结束时，如果 from 是最后一个节点（即其出边链表为空），更新答案 ans。

最重要的是我觉得是head[from] == -1
如果它没有任何出边（即 head[from] == -1），表示它是一个最后一个节点，也就是说它是最终的结束节点，符合最大食物链的定义中的“最右端不会被捕食”。

#include<bits/stdc++.h>
    
using namespace std;
const int N = 5e3 + 5, M = 5e5 + 5, mod = 80112002;
int indep[N], head[N], dp[N], n, m, cnt = 1, ans;
struct Edge {
    int to, next;
} edges[M];

void init () {
    for (int i = 1; i < N; i++) {
        head[i] = -1;
    }
    for (int i = 1; i < M; i++) {
        edges[i].next = -1;
    }
}

void addedge (int from, int to) {
    edges[cnt] = {to, head[from]};
    head[from] = cnt++;
    indep[to]++;
}

void Toposort() {
    queue <int> q;
    for (int i = 1; i <= n; ++i) {
        if (!indep[i]) {
            q.push(i); dp[i] = 1;
        }
    }
    while (!q.empty()) {
        int from = q.front(); 
        q.pop();
        if (head[from] == -1) {
            ans = (ans + dp[from]) % mod;
        }
        for (int to = head[from]; ~to; to = edges[to].next) {
            dp[edges[to].to] = (dp[edges[to].to] + dp[from]) % mod;
            if (--indep[edges[to].to] == 0) {
                q.push(edges[to].to);
            }
        }
    }
    cout << ans;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cin >> n >> m;
    init ();
    for (int i = 1, from, to; i <= m; i++) {
        cin >> from >> to;
        addedge(from, to);
    }
    Toposort(); 
    return 0;
}