优化原理 (1)高斯牛顿 线性

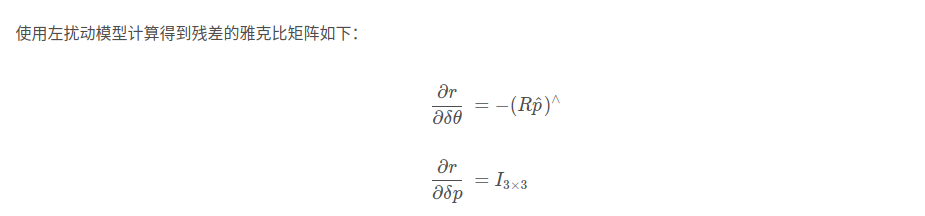
增量方程
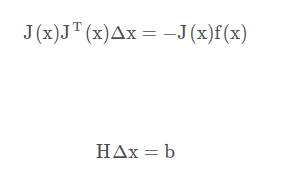

#include <iostream>
#include <Eigen/Core>
#include <Eigen/Dense>
#include <Eigen/Geometry>
#include "sophus/se3.hpp"
#include "sophus/so3.hpp"
int main(void){
// 优化变量为李代数se(3)的平移向量
typedef Eigen::Matrix<double, 6, 1> Vector6d;
// 数据点
std::vector<Eigen::Vector3d> pts1, pts2;
// 随机数生成器
std::default_random_engine generator;
std::normal_distribution<double> noise(0., 1.);
// 构造相机位姿,作为参考位姿
Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix();
Eigen::Vector3d t(1,0,0);
Sophus::SE3d SE3_Rt(R, t);
// 观测数据
for (int i = 0; i < 100; ++i) {
double x = noise(generator), y = noise(generator), z = noise(generator);
pts1.push_back(Eigen::Vector3d(x, y, z)); // 相机坐标系下的点
pts2.push_back(SE3_Rt * pts1[i]); // 世界坐标系下的点
}
// 开始Gauss-Newton迭代,初始位姿为参考位姿+扰动
Sophus::SE3d SE3_estimate(R*Eigen::AngleAxisd(0.1, Eigen::Vector3d::UnitZ()).toRotationMatrix(),
t+Eigen::Vector3d(0.1, 0.0, 0.0));
enum {
DLEFT = 0, // 左扰动
DRIGHT = 1, // 右扰动
};
int disturb = DRIGHT;
for (int iter = 0; iter < 100; ++iter) {
Eigen::Matrix<double, 6, 6> H = Eigen::Matrix<double, 6, 6>::Zero();
Eigen::Matrix<double, 6, 1> b = Eigen::Matrix<double, 6, 1>::Zero();
double cost = 0;
for (int i = 0; i < pts1.size(); ++i) {
// compute cost for pts1[i] and pts2[i]
Eigen::Vector3d p = pts1[i], pc = pts2[i]; // p为相机坐标系下的点,pc为世界坐标系下的点
Eigen::Vector3d pc_est = SE3_estimate * p; // 估计的世界坐标系下的点
Eigen::Vector3d e = pc_est - pc; // 残差
cost += e.squaredNorm() / 2;
// compute jacobian
Eigen::Matrix<double, 3, 6> J = Eigen::Matrix<double, 3, 6>::Zero();
if(disturb == DRIGHT){
// 右扰动
J.block<3,3>(0,0) = Eigen::Matrix3d::Identity();
J.block<3,3>(0,3) = -SE3_estimate.rotationMatrix() * Sophus::SO3d::hat(p);
} else{
// 左扰动
J.block<3,3>(0,0) = Eigen::Matrix3d::Identity();
J.block<3,3>(0,3) = -Sophus::SO3d::hat(SE3_estimate.rotationMatrix() * p);
}
// compute H and b
H += J.transpose() * J;
b += -J.transpose() * e;
}
// solve dx
Vector6d dx = H.ldlt().solve(b);
if (dx.norm() < 1e-6) {
break;
}
// update estimation
if(disturb == DRIGHT){
// 右乘更新
SE3_estimate.so3() = SE3_estimate.so3() * Sophus::SO3d::exp(dx.block<3,1>(3,0));
SE3_estimate.translation() += dx.block<3,1>(0,0);
} else{
// 左乘更新
SE3_estimate.so3() = Sophus::SO3d::exp(dx.block<3,1>(3,0)) * SE3_estimate.so3();
SE3_estimate.translation() += dx.block<3,1>(0,0);
}
std::cout << "iteration " << iter << " cost=" << cost << std::endl;
}
std::cout << "estimated pose: \n" << SE3_estimate.matrix() << std::endl;
std::cout << "ground truth pose: \n" << SE3_Rt.matrix() << std::endl;
}
bug记录
右乘se3的exp映射时,结果有问题,而左乘没问题
初步定位到问题,在求导时,不是对SE3求导,而是对平移向量和旋转向量分别求导,然后再组合起来,这和SE3求导结果不同.
暂时不管了,SE3右乘雅可比有点复杂,高翔书中也是分开求导和更新的,就这样吧。
// se3右乘更新, 有问题 SE3_estimate = SE3_estimate * Sophus::SE3d::exp(dx); // 分开更新,没问题 SE3_estimate.so3() = SE3_estimate.so3() * Sophus::SO3d::exp(dx.block<3,1>(3,0)); SE3_estimate.translation() += dx.block<3,1>(0,0);