OI学习笔记（C++）

Adorable / 2024-07-18 / 原文

笔记完整版链接

参照 oi.wiki 整理了基础 dp 的一些笔记：

学习笔记+模板（Adorable_hly）

（自己结合网络和做题经验总结的，dalao勿喷）

第一大板块：DP

动态规划适用场景：

1. 最优化原理：若该问题所包含的子问题解是最优的，就称该问题具有最优子结构，满足最优化原理。

2. 无后效性：指某一阶段的状态一旦确定，就不受以后决策的影响，换而言之，某状态不会影响之前的状态，只与当前状态有关。

3. 有重叠子问题：子问题之间不独立，一次决策可能会在往后的决策中多次使用（这一条是动规相较于其他算法的最大优势，是dp的必要条件）。

动态规划五大要素：

1. 状态

2. 状态转移方程

3. 普遍决策

4. 初始状态

5. 边界条件

背包dp

一，01背包

例题（模板）：

题意概要：有 $n$ 个物品和一个容量为 $W$ 的背包，每个物品有重量 $w_{i}$ 和价值 $v_{i}$ 两种属性，要求选若干物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量。

对于每种物品，我们有取（1）与不取（0）两种策略，所以称为01背包问题。

状态：设一个 $dp[i][j] → dp_{i,j} $ 数组，表示只考虑前 $i$ 个物品的情况下（考虑，不一定放，表示最优解），容量为 $j$ 的背包可以获得的最大总价值。

状态转移方程：对于第i个物品，考虑两种决策：

不放入背包，背包总量保持上一步不变，即 $dp_{i,j} = dp_{i-1,j}$
放入背包，背包容量减少 $w_i$ ，加入新物品的价值 $v_i$ ,即 $dp_{i,j} = dp_{i-1,j-w_i} + v_i$
综上，可以得出状态转移方程（考虑最优，所以取最大值）

\[dp_{i,j} = max(dp_{i-1,j},dp_{i-1,j-w_i}+v_i) \]

当然，还要加上判断，当 $j \ge w_i$ 时，才能取决策二，否则 $dp$ 的第一维可能会变成负数。

但是，如果直接用二维数组表示状态，会 MLE（即爆内存），应考虑用滚动数组的形式来优化（减少一维）。

因为在本题中，状态数组中只有上一次的决策被使用，所以
不用把每次的 $dp_{i-1,j}$ 都记录下来，可以减少一维，直接用 $dp_{i}$ 来表示处理到当前物品时背包容量为 $i$ 的最大价值，得到：

\[dp_{j} = max(dp_{j-1},dp_{j-w_i}+v_i) \]

模板：

for (int i = 1;i<=n;++i)
  for (int j = W;j>=w[i];--j) //不要写递增的
    f[j] = max(f[j],f[j - w[i]] + v[i]);

二，完全背包

与01背包类似，不同点在于完全背包每件物品有无限个，即可以选无限次，二01背包每件物品只能选一次。

状态：设 $dp_{i,j}$ 为只能选前 i 个物品时，容量为 j 的背包可以达到的最大价值。

最暴力的 $dp$ 就是和01背包思路差不多的， $k$ 为拿的数量，一个个枚举来转移，方程如下：

\[dp_{i,j}=\max_{k=0}^{+\infty}(dp_{i-1,j-k\times w_i}+v_i\times k) \]

这个做法的复杂度为：$O(n^3)$

↑ 理解了， ↓ 没理解

考虑一下优化，引用自 oi.wki-完全背包 (略微改动)

没理解优化，但是还是背下来吧:

考虑做一个简单的优化。可以发现，对于 $f_{i,j}$，只要通过 $f_{i,j-w_i}$ 转移就可以了。因此状态转移方程为：

\[dp_{i,j}=\max(dp_{i-1,j},dp_{i,j-w_i}+v_i) \]

理由是当我们这样转移时，$dp_{i,j-w_i}$ 已经由 $dp_{i,j-2\times w_i}$ 更新过，那么 $dp_{i,j-w_i}$ 就是充分考虑了第 i 件物品所选次

例题（模板）：

题意概要：有 $n$ 种物品和一个容量为 $W$ 的背包，每种物品有重量 $w_{i}$ 和价值 $v_{i}$ 两种属性，要求选若干个物品放入背包使背包中物品的总价值最大且背包中物品的总重量不超过背包的容量。

例题代码
#include<bits/stdc++.h>
using namespace std;

const int maxn = 1e4+5,maxm = 1e7+5;
int n, W, w[maxn], v[maxn];
long long dp[maxm];

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	cin>>W>>n;
	for(int i = 1; i<=n;++i) cin>>w[i]>>v[i];
	for(int i = 1; i<=n;++i)
		for(int j = w[i];j<=W;j++)
			if(dp[j-w[i]]+v[i]>dp[j]) dp[j]=dp[j-w[i]]+v[i];
	cout<<dp[W]<<endl;
	return 0;
}

dp未完待续……

第二大板块：树状数组

一，概念
手搓了两张草图：
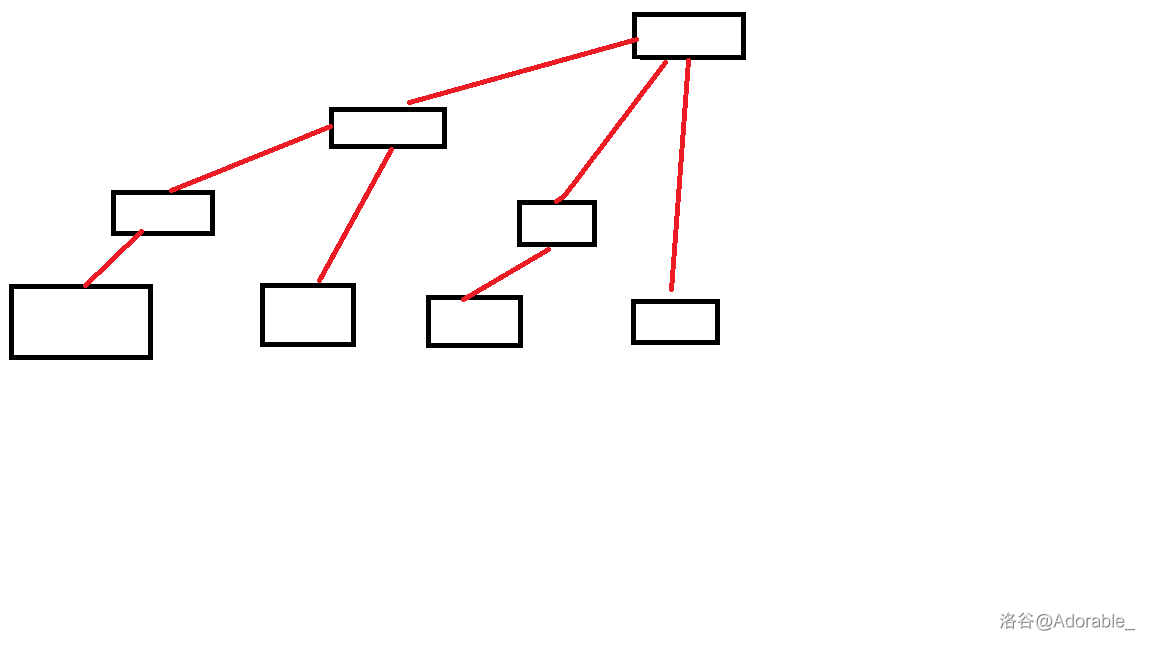图一 ↑ ↑ ↑

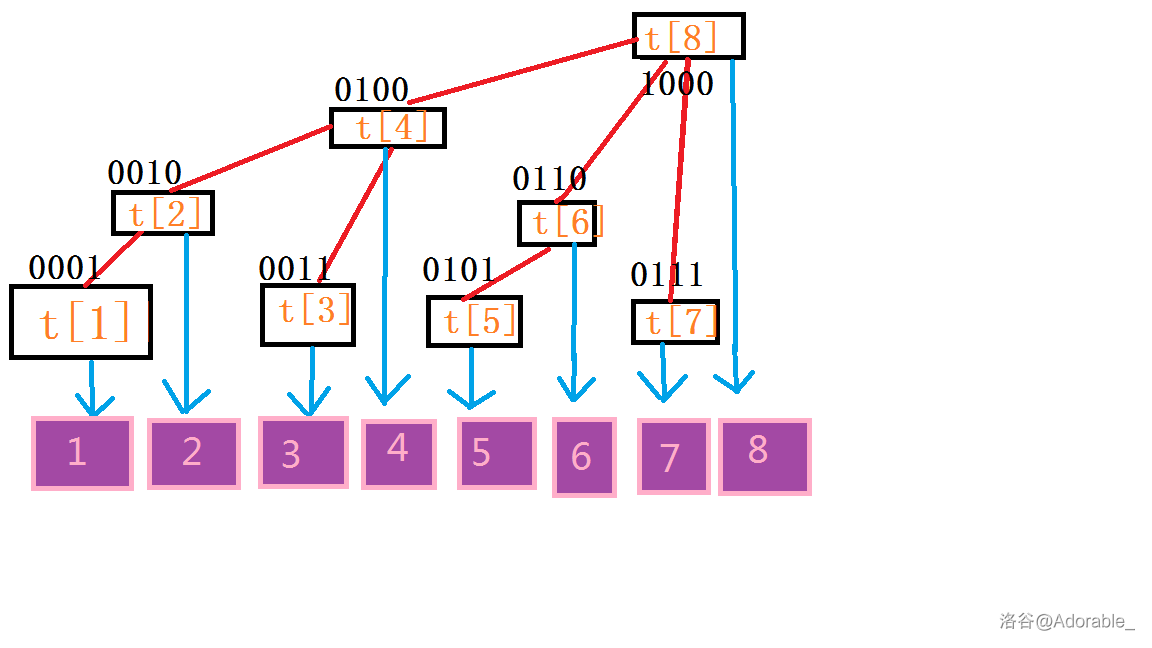图二 ↑ ↑ ↑（请不要在意颜色，瞎整的）

关于储存大概就是这个结构，和线段树的功能有点像。

功能：

单点修改，单点查询(这个就不要需要树状数组了)
区间修改，单点查询（本版块重点）
单点修改，区间查询（本版块重点）
区间修改，区间查询（建议线段树实现）
等等

优点：相较于线段树好写，省时省力（杀鸡焉用宰牛刀， ~~而且我现在也不会线段树~~ ）。

缺点：扩展性弱，换而言之，线段树能解决的问题用树状数组可以解决大部分，但不是全部。

先记一下 lowbit 的用法：

计算非负整数 n 在二进制下，从右到左第一个1到最右边构成的数，等价于删去从左到右最后一个1到最左边所有的数（最后一个1不删）

例如：

a = 1010100;
lowbit(a) = 100;//删去了左边的“1010”

实现：对 $(x)_2$ 取反，再与原数 $(x)_2$ 进行按位与运算。
写法1：

int lowbit(int x)
{ return ((x)&(-x)); }//因为篇幅，稍微压一下行

写法2：

#define lowbit(x) ((x)&(-x))

注：带一堆括号只是为了保险 ~~（虽然我也知道没必要，但写上肯定不会错）~~

如图2，用t[i]表示以x为根的子数中叶子节点值的和，原数组为a[]。容易发现：

\[t_4 = t_2+t_3+a_4 = t_1+a_2+t_3+a_4 = a_1+a_2+a_3+a_4 \]

观察一下二进制数，发现每一层末尾的0个数是相通的（可能我画的不太形象，第一层是 $t_1,t_3,t_5,t_7$,第二层是 $t_2,t_6$ ,第三层是 $t_4$ ,第四层是 $t_8$ ）

再观察，树状数组中节点x的父亲节点为 x + lowbit(x)
eg:对于 t[2] (父亲节点为 t[4] )，

\[t[4] = t[2+lowbit(2)] , 4 = 2+lowbit(2) \]

原理大致介绍完了，记一下例题吧

例题

洛谷P3374 树状数组模板1

大意：输入n，m（该数列数字的个数和操作的总个数）
输入n个数表示第 i 项的初始值。
接下来 m 行每行包含 3 个整数，表示一个操作:
1 x k 含义：将第 x 个数加上 k
2 x y 含义：输出区间 [x,y] 内每个数的和

对于每次2操作输出一次区间和。

一道很板的题，要考虑两个：单点修改和区间查询

1. 单点修改，区间查询

1.1 单点修改

单点修改时，可以吧 t[i]理解为前缀和，例如，如果我们对 a[1]+k，那么对于 t[1],t[2],t[4],t[8]（即全部祖先）都需要+k更新，此时就可以使用上面关于 lowbit 的结论了，

模板：

int add(int x,int k)//对第x项进行+k操作
{
  for(int i = x;i<=n;i+=lowbit(i))
    t[i]+=k;
}

1.2 区间查询

我们先找例子，再由一般到特殊：
eg:查询 1~7的和

还是从图2，很容易看出：答案就是 $t[7]+t[6]+t[4]$

进一步观察，

\[6 = 7-lowbit(7),4 = 6-lowbit(6) \]

所以可以循环不断 -lowbit(),一直减到最底层来实现

int sumout(x)
{
	int sum = 0;
	for(int i=x;i;i-=lowbit(i))
		sum+=t[i];
	return sum;
}//算了压行码风太丑，就不了。。。

这个模板只能求区间 [1，x] 的和，当然求 [l,r] 的区间和基本同理，利用前缀和相减的性质就可以了，

\[[l,r] = [1,r]-[1,l-1] \]

实现1：
利用上述函数

return sumout(1,r)-sumout(1,l-1);

实现2：

~~重新手搓一个~~
也是前缀和思想，同上

int sumout(int l,int r)
{
	int sum = 0;
	for(int i = r;i;i-=lowbit(i)) sum+=t[i];
	for(int i = l-1;i;i-=lowbit(i)) sum-=t[i];
	return sum;
}

洛谷P3368 树状数组模板2

2. 区间修改，单点查询

2.1 区间修改

差分的原理，构造一个差分数组 c，用树状数组维护 c 即可，利用差分数组的性质，只需要更新 $add(l,k),add(r+1,-k)$ 即可

模板：

void change(int loc,int k)//把loc及其后面的点+k
{
  for(int i = loc;i<=n;i+=lowbit(i))
    	c[i]+=k;
}

实现：

change(l,k);
change(r+1,-k);

2.2 单点查询

单点查询即求出 c 的前缀和即可；

$a[x] = c[1] + c[2] + ... + c[x]的前缀和$（依据差分数组的性质）

int findd(int loc)
{
	int ans = 0;
  for(int i = loc;i;i-=lowbit(i)) ans+=c[i];
  return ans;
}

lowbit 原理同上

3.区间修改，区间查询

用树状数组过于复杂，建议使用线段树 ~~（虽然我不会）~~