杂题选解

zhengzirui / 2023-05-13 / 原文

模拟

L-shapes

模拟、图形模拟

L-shapes - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

Problem - F - Codeforces

题解较复杂Codeforces Round #817 (Div. 4) Editorial - Codeforces

代码实现比较难，要多写几遍

Submission #205513970 - Codeforces

矩阵旋转

图形模拟

码题集OJ-迷宫 (matiji.net)

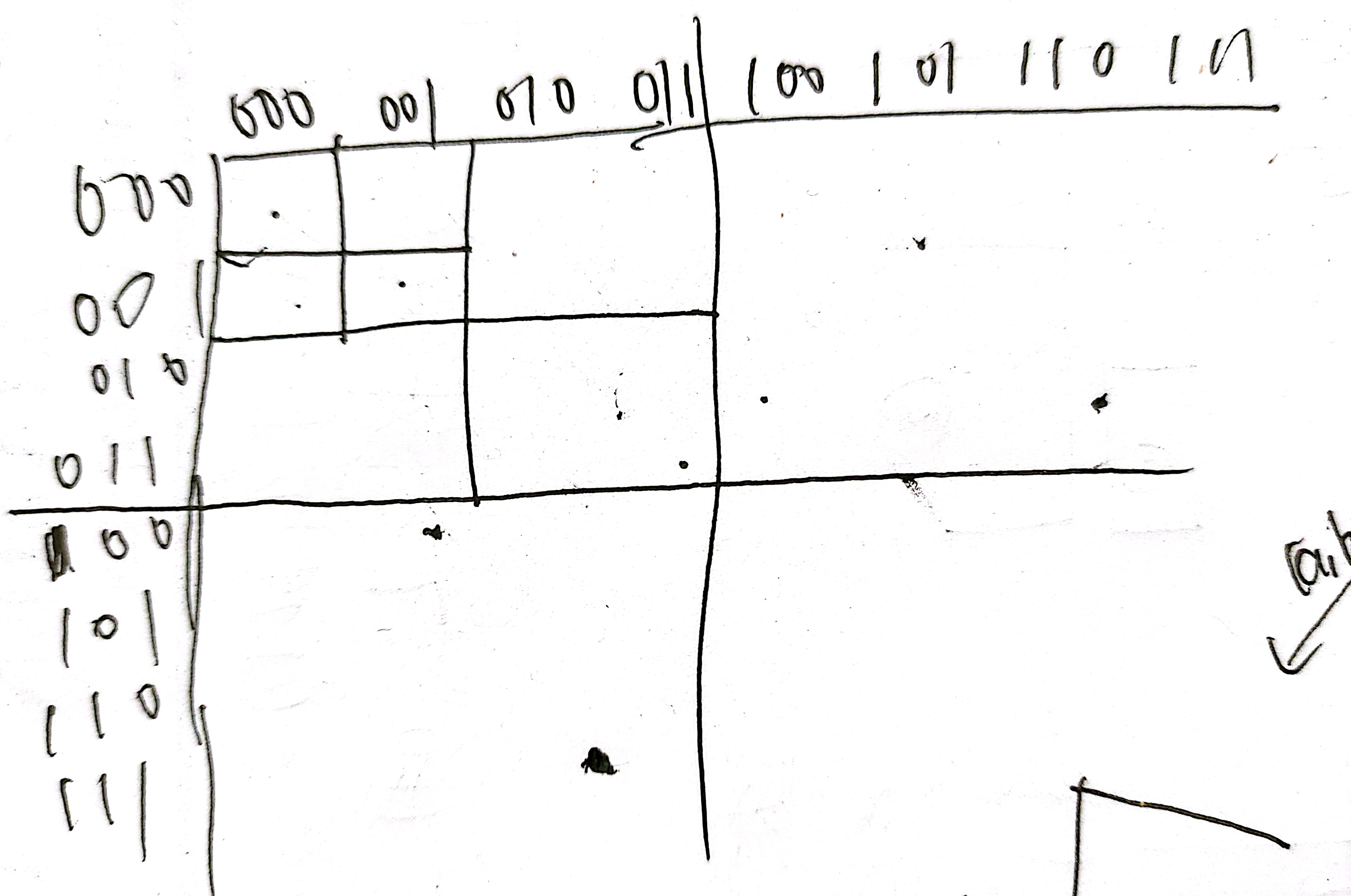
对于n阶矩阵，行号和列号从0~2^n-1，用二进制表示发现，如果横纵坐标的最高位都为0，则在n阶矩阵的左上区域，其他同理。

所以，对于n阶矩阵中位置为(x, y)的点：

首先由最高位求出它在n阶矩阵的哪个区域
观察可以发现剩余位是它在n-1阶矩阵中的位置。也就是说当n-1阶矩阵没有旋转时，n阶矩阵中(x, y)的符号和n-1阶矩阵中(tx, ty)的符号相同。如果旋转了，则已旋转的n-1阶矩阵中(tx, ty)的符号应该是原n-1阶矩阵中(tx', ty')的符号+k (k = 1, 2, 3)。
通过以上分析，结合递归函数的定义，它返回的是未旋转的n阶矩阵中(x, y)位置的值，如果是已知旋转后矩阵的x,y，则要反推出原矩阵的x,y作为函数的参数。且元素旋转后自身也要变，顺时针旋转90度在mark数组中的下标就对应+1。
递归出口是0阶矩阵时，返回的是0，表示它是mark矩阵中下标为0的元素>。

技巧：图像旋转问题，只要算出90度，180,270只需做2,3次90即可。

一种方便的做法是创建一个备份数组，在原数组中用坐标变换公式算出每一个(x, y)是谁转过来的。

坐标变换公式的推导要抓住：同一列的元素旋转之后一定在同一行，同一行的元素旋转之后一定在同一列。

关于矩阵旋转的相关题目：

3212. 图像旋转 - AcWing题库

3527. 旋转矩阵 - AcWing题库

#include <bits/stdc++.h>
using namespace std;

using ll = long long;
using pii = pair<int, int>;
char mark[] = ">v<^";

int calc(int x, int y, int n) // 返回在n阶矩阵中(x, y)这个位置的符号在mark数组中的下标
{
    int dx = x >> (n - 1) & 1, dy = y >> (n - 1) & 1; // 
    int m = 1 << (n - 1);
    int tx = x & (m - 1), ty = y & (m - 1);
    if (n == 0) return 0;
    if (dx == 0 && dy == 0) return calc(tx, ty, n - 1);
    else if (dx == 1 && dy == 0) return calc(m - 1 - ty, tx, n - 1) + 1;
    else if (dx == 0 && dy == 1) return calc(m - 1 - tx, m - 1 - ty, n - 1) + 2;
    else if (dx == 1 && dy == 1) return calc(ty, m - 1 - tx, n - 1) + 3;
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);

    int n;
    cin >> n;
    for (int i = 0; i < (1 << n); i ++ , cout << "\n")
        for (int j = 0; j < (1 << n); j ++ )
            cout << mark[calc(i, j, n) % 4];
    return 0;
}

Water Level

模拟、贪心、技巧

Water Level - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

Problem - E - Codeforces

题目大意

 有一个水桶，水桶里面有k升水，我们每天开始的时候可以往里面注入y升水，每天的消耗量是x升，问我们能否使水量在[l,r]范围内保持t天

解析

一个技巧：每轮减小\(x\)，由\(r\)减小到\(l\)需要\((r - l) / x\)轮 [下取整，算的是间隔数而不是点数]

分类讨论

x > y
- 说明水量会单调递减，则最多坚持\((k - l) / (x - y)\)天
- 特判：如果第一天加水会超过r，则第一天不加，因为只要减少一次x后，加水就不会溢出了
x <= y
- 目的是让水位保持在[l, r]之间，所以最好的方法是当水位要小于\(l\)时才加水，这是因为\(y > x\)，只要加水就一定不会减到低于\(l\)了，而且只在必要时加水也能减少溢出的概率(贪心)
- 所以我们的做法是：先将水减到不能再减，判断此时的剩余天数。
  - 天数<=0，说明成功维持了\(t\)天
  - 否则，在接下来的一天：加水，判断是否溢出、减水
- 一个优化：当剩余水量出现循环时，说明从上一次到达这个水位开始都能维持住，那接下来同样也是循环，一定能维持住
  - 判断循环：\(k1 \% x == k2 \% x\)。k1 = k2时，显然；k1 != k2，由于两者之间差x的整数倍，只需要再减这么多天的水即可相等，所以也认为是出现了循环。

AC代码：Submission #205511487 - Codeforces

二分

Scuza

二分

Problem - E - Codeforces

Scuza - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

要点：

二分要注意上溢和下溢，可以设在两边设哨兵或者错位存储下标对应的答案。
要在数列a中找到从左数第一个大于k的数的位置：构造数列m，m[i] = max(a[1 ~ i])，也就是a数列的前n项最大值数列，然后在m中二分找到第一个大于k的数即可。

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

void solve()
{
    vector<ll> pref; // 前缀和数组
    pref.push_back(0);
    vector<int> prefmax; // 前n项最大值数组
    prefmax.push_back(0); // 设置下溢的哨兵
    int n, q;
    cin >> n >> q;
    for (int i = 0; i < n; i ++ )
    {
        int x;
        cin >> x;
        pref.push_back(pref.back() + x);
        prefmax.push_back(max(prefmax.back(), x));
    }
    while (q -- )
    {
        int k;
        cin >> k;
        int ind = upper_bound(prefmax.begin(), prefmax.end(), k) - prefmax.begin();
        cout << pref[ind - 1] << " ";
    }
    cout << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);

    int n;
    cin >> n;
    while (n -- ) 
        solve();
}

数学

Coprime

数论、暴力、技巧

Problem - D - Codeforces

Coprime - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

要点：当数据的特点是范围小（数值类型）而个数多时，可以考虑对数据大小范围内的所有实数做暴力，而不是对输入的数据做暴力

// 注意到，数组最多有1000个不同的元素，因为a<=1000。对于每个值，存储它所在的最大索引。然后我们可以枚举1000以内所有互质的数，然后再判断这两个数是否在数列中。若在，就将答案更新。
#include <bits/stdc++.h>
using namespace std;

const int N = 1010;
void solve()
{
    int idx[N]{};
    int m;
    cin >> m;
    for (int i = 1; i <= m; i ++ )
    {
        int x; 
        cin >> x;
        idx[x] = max(idx[x], i);
    }
    int ans = 0;
    for (int i = 1; i <= 1000; i ++ )
    {
        if (!idx[i]) continue;
        for (int j = 1000; j >= i; j -- )
        {
            if (idx[j] && __gcd(i, j) == 1)
            {
                ans = max(ans, idx[i] + idx[j]);
            }
        }
    }
    if (!ans) cout << -1 << endl;
    else cout << ans << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n;
    cin >> n;
    while (n -- ) 
        solve();
}

位运算

Orray

或运算、暴力、结论

Orray - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

Problem - G - Codeforces

【位运算暴力】CF1742G Orray - 一扶苏一的博客 - 洛谷博客 (luogu.com.cn)

要点：算术操作“按位或”是没有进位的，且保证两个数按位或起来一定大于等于原先的两个数，所以有结论：

具体做法：

// 暴力从没有用过的数中找出使得新的前缀或运算结果最大的数，将它输出。做log2(a_max)次即可。最后将剩下的直接输出。
#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10;

void solve()
{
    int a[N]{};
    bool vis[N]{};
    int n;
    cin >> n;
    for (int i = 0; i < n; i ++ ) cin >> a[i];

    int cur_or = 0;
    for (int i = 0; i < min(n, 31); i ++ )
    {
        int mx = 0, idx = 0;
        for (int j = 0; j < n; j ++ )
        {
            if (vis[j]) continue;
            if ((cur_or | a[j]) > mx) mx = cur_or | a[j], idx = j; // 特别注意：位运算的优先级比大于号低，要加括号。以后碰到位运算和比较运算符在一起都要加括号，防止出错
        }
        vis[idx] = true;
        cout << a[idx] << " ";
        cur_or |= a[idx];
    }
    for (int i = 0; i < n; i ++ ) if (!vis[i]) cout << a[i] <<  ' ';
    cout << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);

    int n;
    cin >> n;
    while (n -- ) 
        solve();
}

Even-Odd XOR

异或、结论、构造

Even-Odd XOR - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

Problem - G - Codeforces

要点：

异或运算的定义和运算律
- 定义：0 ^ 0 = 0, 0 ^ 1 = 1, 1 ^ 0 = 1, 1 ^ 1 = 0
- 运算律：
  1. 一个值与自身的运算，总是为 false，即x^x=0
  2. 一个值与 0 的运算，总是等于其本身，即x^0=x
  3. 交换律，x^y=y^x
  4. 结合律，(x^y)^z=x^(y^z)
定理：奇数和偶数位置异或和相等的充要条件是全局异或和为 0

证明：设奇数和偶数位置的异或和分别为a,b,全局异或和为g

\(g=0 \Leftrightarrow a\wedge b=0 \Leftrightarrow a=b\)

综上：只需保证全局异或和为0即可

一种构造方式是：

前n-3个数为1,2,3,...,n-3，第n-2个数为\(2^{29}\)，第n-1个数为\(2^{30}\)，第n个数为所有前n-1个数的异或和。

这种方法可以保证：

全局异或和为0，因为前n-1项与第n项的异或和为0
每个数互不相同

证明：首先前n-3个数互不相同，且因为n<2e5<2^29，所以前n-1个数都互不相同。\(a_{n-2}是2^{29}级别的，a_{n-1}是2^{30}级别的，\\根据异或运算的定义，a_{n}是2^{29}+2^{30}级别，所以a_{n}比前n-1个数都大\)

#include <bits/stdc++.h>
using namespace std;


void solve()
{
    int n;
    cin >> n;
    int xsum = 0;
    for (int i = 1; i <= n - 3; i ++ )
    {
        cout << i << ' ';
        xsum ^= i;
    }
    cout << (1 << 29) << ' ' << (1 << 30) << ' ' << (xsum ^ (1 << 29) ^ (1 << 30)) << "\n";
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);

    int n;
    cin >> n;
    while (n -- ) 
        solve();
    return 0;
}

构造

Smaller

构造、字符串

Problem - F - Codeforces

Smaller - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

要点：构造算法

不难发现，如果 t 中有一个字符不是 a，那么只要把那个字符移到第一位，就可以满足 s 的字典序小于 t，而如果两个字符串中都只有 a 的话，那就只要比较两个字符串的大小就好了

AC代码

计算几何

水渠规划

计算几何、点到线段的距离

码题集OJ-水渠规划 (matiji.net)

点到三角形的最短距离就是点到三角形的三条线段的距离中最小的那个。

所以只需分别求出点到三条线段的距离，取最小的那个即可。

AC代码

图论

城市通电

最小生成树、超级源点

3728. 城市通电 - AcWing题库

解析

题目有两种费用
- 每个点之间的边的费用
- 建立发电站的费用
这是一道最小生成树中超级源点的模板题，核心就是将假设有一个“超级源点”，将建立发电站的费用转化为每个点到“超级源点”的边的费用，则原题就可以转化为求增加了超级源点后的最小生成树的大小和方案。
Prim算法求方案：在更新dist变小时distp记录是哪个点让它变小的，那个点就可能是这个点在最小生成树中的一个邻点。最终当一个点纳入最小生成树集合时的distp就是邻点。

AC代码：code

道路与航线

最短路，dijkstra、拓扑排序

P3008 Roads and Planes G - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

342. 道路与航线 - AcWing题库

题目大意

一张图满足：

无向边权值非负，双向
有向边权值可正可负，单向，如果存在一条从A到B的有向边，保证不可能通过一些无向边和有向边从B到A（无环）

求一个点到其他所有点的最短路

解析

这题要求的是带负权边的最短路，显然不能直接用Dijkstra。然而Bellman-Ford或SPFA的时间复杂度最坏O(N**M*)，尽管这题数据比较老，因此SPFA+SLF可以水过，但是正解并不是如此。

可以发现，图有一个很强的性质：对于无向边，边权总是正的，因此每个无向边联通块是强联通的。而可能的负权边保证不能反向联通，因此把无向边联通块缩点后，得到的就是DAG。这样就可以在块内使用Dijkstra，块间利用拓扑排序更新答案。时间复杂度O(MlogN + M + N)。

正确性

对于每个点，都是通过它的邻点更新它的dist值，块内的Dijkstra用与它无向边相邻的点更新，块间的拓扑排序用与它有向边相邻的点更新，因此最后得到的dist值就是最小的。

对Dijkstra的理解：原来都是在一个图内做dijkstra，从源点S出发更新邻点的dist值。其实该算法的本质就是用一个点的dist值来更新它的所有邻点的dist值，因此块内的dijkstra做法是

让块内所有点入队
取出dist最小的（不一定是源点），更新它的邻点
如果邻点是块内的点，则入队。如此往复，直到队列为空。
细节：当一个点从队列中取出来时，它的dist值已经达到最小（有向边和无向边都更新完成）。开一个全局的st数组，将这样的点标记为true，之后再遇到它时跳过。

对拓扑排序的理解：拓扑排序求最短路的状态转移方程是\(dist[son] = min(dist[son], dist[father] + w)\)，与dijkstra的更新方式一样。做法是

无论邻点是不是块内的点，都松弛。
如果是其他块的点，则那一块的入度减1。
一个连通块的入度减为0时，入拓扑排序的队列

AC代码：342. 道路与航线 - AcWing题库

最长路

拓扑排序

解析

在有向无环图(DAG)中，可以用拓扑排序来找最短路和最长路，复杂度是\(O(n + m)\)，边权可正可负。

做法：

将dist初始化为0xcfcfcfcf，方便之后的更新
把除1以外入度为0的点以及删去它们的出边后产生的新的入度为0的点的出边都删去。
在拓扑排序时更新\(dist[son] = max(dist[son], dist[father] + w)\)

AC代码：记录详情 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

动态规划

厦大GPA

分组背包、dfs、技巧、贪心

题目大意

每门考试成绩为百分制，则分数与绩点对应关系如下:
90~100 4.0
85~89 3.7
81~84 3.3
78~80 3.0
75~77 2.7
72~74 2.3
68~71 2.0
64~67 1.7
60~63 1.0
0~59 0.0
某位同学一共参加了4门考试，给定四门考试的总分，请问在最优情况下，4门考试绩点的和最高是多少?

解析

这道题有两种做法

直接深搜枚举四个数，可以选择的优化方案
- 从大到小枚举四个数，保证方案不重复枚举
- 当\(score + 4 * (4 - u) <= ans\)，返回，最优化剪枝
- 当所剩分数<=0时更新答案返回
云剪贴板 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

这个做法的时间是\(581ms\)
看成有4个组和一个容量为总分的背包，每组可选的物品是分数。体积是分数值，价值是对应的绩点，每组只能选一个，求最大价值。这是一个分组背包问题。
- 普通写法：每组的物品就是从1分到100分，用函数算出对应的GPA即可。\(157ms\)
  
  云剪贴板 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
- 技巧与优化：注意到题目中的分数在一个区间内的价值相同，那么每次只需要枚举每个区间的最低分数即可。这样既能保证价值最大，又为其他组空出尽可能多的空间，是最优解。并且这种方式可以查表实现，大大提速。\(4ms\)
  
  云剪贴板 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)