寻宝

题目大意

存在 \(n\) 个点和两种有向边：

• 一类边分 \(m\) 组，每组的边权相同，从 \([s_l,s_r]\) 中的所有点连向 \([t_l,t_r]\) 中的所有点。

• 二类边存在于任意两点 \(i,j\) 间，从 \(i\) 连向 \(j\) 的二类边的边权为 \(|i-j|\times a_i\)。

求从点 \(1\) 到 \(n\) 的最短路及方案。

思路分析

神仙题。

一类边比较好处理，可以直接用区间向区间连边的线段树优化建图加 Dijkstra 搞定。具体可以看 P6348 Journeys，因此主要看二类边。

思考 Dijkstra 的过程：

• 找到没有更新过其他点的距离最小的点。

• 用这个点更新所有能够到达的点。

我们发现，每一个点都可以通过二类边到达其他所有点，因此可以不建出二类边，而只考虑二类边造成的影响。

设当前的点为 \(u\)，不难发现，如果以连向的点的编号为横坐标，距离为纵坐标，那么通过 \(u\) 连向 \(v\) 的二类边对 \(v\) 更新的距离在坐标系上形成两条线段，右侧线段的斜率为 \(a_i\)，截距为 \(dis_{u}-u\times a_u\)，定义域为 \((u,n]\)，左侧线段的斜率为 \(-a_i\)，截距为 \(dis_{u}+u\times a_u\)，定义域为 \([1,u)\)。

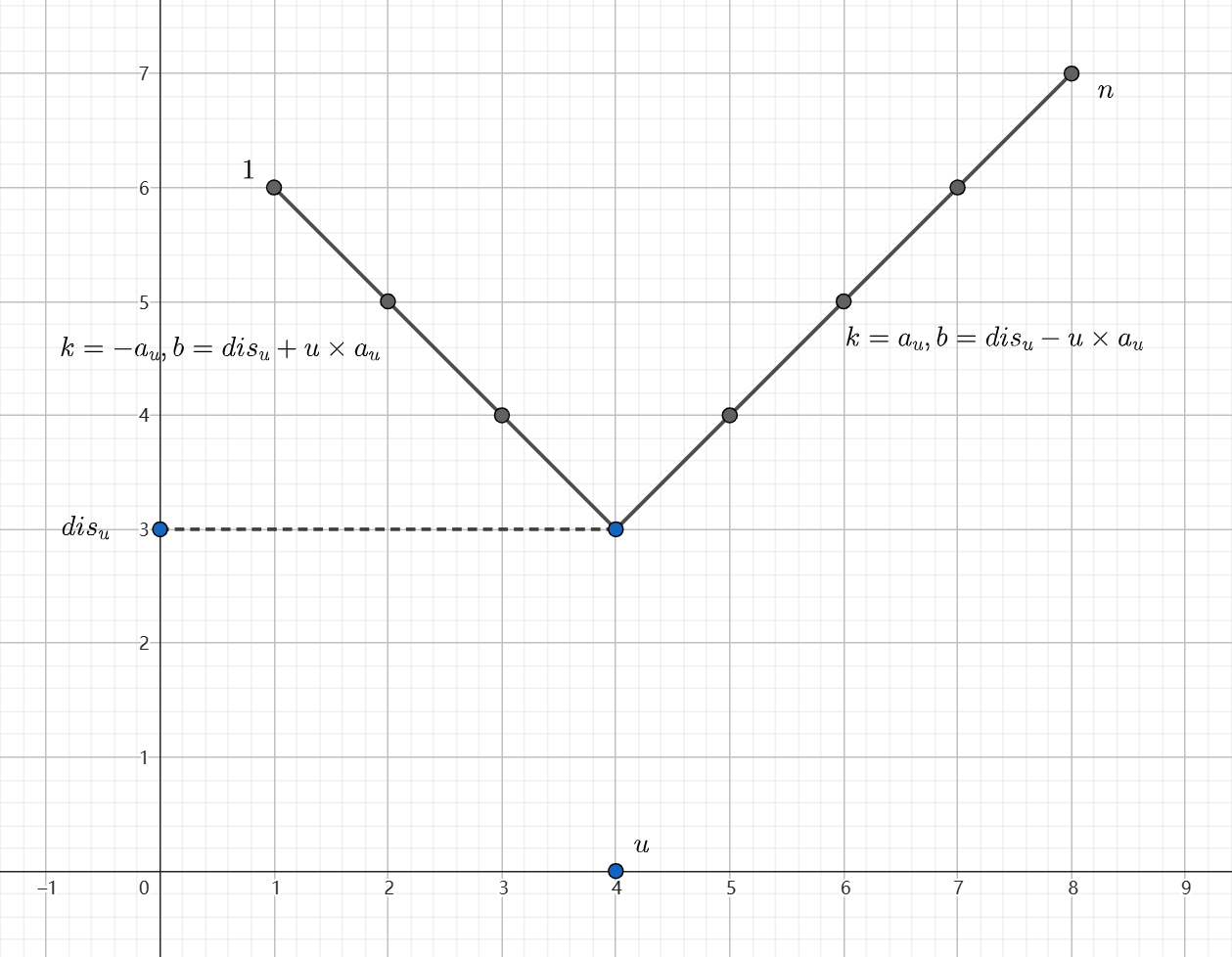
因此，二类边实际上是对于对于每个点将其当前距离与一条线段取 \(\min\)。

那么这就可以用李超线段树维护。

具体的说，我们实现一颗拥有堆的功能的李超线段树，也就是支持单点删除，查询全局最小值及位置，区间对线段取 \(\min\)。

在 Dijkstra 时按照以下过程进行：

• 比较堆中的最小值和李超线段树中的最小值，取出并删除较小的一个。

• 用取出的点通过线段树优化建图建出的边对所有能到达的点进行更新。

• 如果该点的 \(a_i\not =0\)，那么向李超线段树中添加上述的两条线段。

这样我们就可以完成最短路的求值，考虑到点数是 \(O(n)\) 的，边数是 \(O(n\log n)\) 的，李超线段树单次插入线段是 \(O(\log^2 n)\) 的，故时间复杂度为 \(O(n\log^2 n)\)。

方案就比较简单了，用一类边更新的点可以直接记录方案，用二类边更新的点可以在插入线段时顺便记录此线段的来源，然后从 \(n\) 逆推即可。

代码

（只有 5k，算短的了）

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
#include <cmath>
#include <queue>

using namespace std;
const int N=600000,M=200200;
#define inf 0x3f3f3f3f3f3f3f3f
#define mid ((l+r)>>1)
typedef long long ll;

int n,m,in1,in2,in3,in4,in5,L,K,num,tot;
int vis[N],from[N];
ll dis[N],a[N];

struct Node{
    int x;ll dis;
    bool operator < (Node a) const {
        return dis>a.dis;
    }
};

struct Line{
    ll k,b;
}line[N];

vector<pair<int,int>> to[N]; 
vector<int> ans;
priority_queue<Node> q;

void add(int u,int v,int w){
    to[u].push_back({v,w});
}

ll calc(int id,int x){
    return line[id].k*x+line[id].b;
}

bool Less(int id1,int id2,int x){
    return calc(id1,x)<calc(id2,x);
}

struct ST1{
    void build(int p,int l,int r){
        if(l==r){add(p+L,l,0);add(l,p+K,0);return ;}
        build(p<<1,l,mid);build(p<<1|1,mid+1,r);
        add(p+L,(p<<1)+L,0);add(p+L,(p<<1|1)+L,0);
        add((p<<1)+K,p+K,0);add((p<<1|1)+K,p+K,0);
    }
    void addedge(int p,int l,int r,int x,int y,int k,int f){
        if(x<=l&&r<=y) return add(f?k:p+K,f?p+L:k,0);
        if(x<=mid) addedge(p<<1,l,mid,x,y,k,f);
        if(y>mid) addedge(p<<1|1,mid+1,r,x,y,k,f);
    }
}tree1;

void addedge(int l1,int r1,int l2,int r2,ll w){
    tree1.addedge(1,1,n,l1,r1,num,0);
    tree1.addedge(1,1,n,l2,r2,num+1,1);
    add(num,num+1,w);num+=2;
}

struct ST2n{
    int L,R,from;
    ll min;
    int id,del;
}res;
struct ST2{
    ST2n a[M];
    void del_t(int p){
        a[p].del=1;a[p].min=inf;
    }
    void push_up(int p,int l,int r){
        if(a[p].del) return ;
        if(l==r){a[p].min=calc(a[p].id,l);return ;}
        if(a[p<<1].del&&a[p<<1|1].del) return del_t(p);
        a[p].L=a[p<<1].del?a[p<<1|1].L:a[p<<1].L;
        a[p].R=a[p<<1|1].del?a[p<<1].R:a[p<<1|1].R;
        a[p].min=min(a[p<<1].min,a[p<<1|1].min);
        a[p].min=min({a[p].min,calc(a[p].id,a[p].L),calc(a[p].id,a[p].R)});
    }
    void build(int p,int l,int r){
        a[p]={l,r,0,inf,0,0};
        if(l==r) return ;
        build(p<<1,l,mid);build(p<<1|1,mid+1,r);
    }
    void update(int p,int l,int r,int id,int f){
        if(a[p].del) return ;
        if(!a[p].id){a[p].id=id;a[p].from=f;return push_up(p,l,r);}
        if(Less(a[p].id,id,a[p].L)&&Less(a[p].id,id,a[p].R)) return ;
        if(Less(id,a[p].id,a[p].L)&&Less(id,a[p].id,a[p].R)){
            a[p].id=id;a[p].from=f;return push_up(p,l,r);
        }
        if(Less(id,a[p].id,mid)) swap(id,a[p].id),swap(f,a[p].from);
        if(Less(id,a[p].id,a[p].L)) update(p<<1,l,mid,id,f);
        if(Less(id,a[p].id,a[p].R)) update(p<<1|1,mid+1,r,id,f);
        return push_up(p,l,r);
    }
    void push_down(int p,int l,int r){
        if(a[p].del||!a[p].id||l==r) return ;
        update(p<<1,l,mid,a[p].id,a[p].from);
        update(p<<1|1,mid+1,r,a[p].id,a[p].from);
        a[p].id=0;a[p].from=0;
        return push_up(p,l,r);
    }
    void add(int p,int l,int r,int x,int y,int id,int f){
        if(a[p].del) return ;
        if(x<=l&&r<=y) return update(p,l,r,id,f);
        push_down(p,l,r);
        if(x<=mid) add(p<<1,l,mid,x,y,id,f);
        if(y>mid) add(p<<1|1,mid+1,r,x,y,id,f);
        push_up(p,l,r);
    }
    void get(int p,int l,int r){
        if(l==r){res=a[p];return del_t(p);}
        push_down(p,l,r);
        if(a[p<<1|1].del||a[p<<1].min<a[p<<1|1].min) get(p<<1,l,mid);
        else get(p<<1|1,mid+1,r);
        push_up(p,l,r);
    }
}tree2;

void addline(int l,int r,ll k,ll b,int f){
    line[++tot]=Line{k,b};
    tree2.add(1,1,n,l,r,tot,f);
}

void Dijkstra(){
    memset(dis,0x3f,sizeof dis);
    q.push(Node{1,0});dis[1]=0;
    while(!q.empty()||tree2.a[1].min!=inf){
        int now;
        if(q.empty()||tree2.a[1].min<q.top().dis){
            tree2.get(1,1,n);
            now=res.L;
            if(vis[now]) continue;
            dis[now]=res.min;
            from[now]=res.from;
        }
        else now=q.top().x,q.pop();
        if(vis[now]) continue;
        vis[now]=1;
        for(auto [v,w]:to[now]){
            if(dis[v]<=dis[now]+w) continue;
            dis[v]=dis[now]+w;from[v]=now;
            q.push(Node{v,dis[v]});
        }
        if(now<=n&&a[now]){
            if(now!=1) addline(1,now-1,-a[now],dis[now]+a[now]*now,now);
            if(now!=n) addline(now+1,n,a[now],dis[now]-a[now]*now,now);
        }
    }
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
    L=n;K=5*n;num=9*n+1;
    line[0]={0,inf};
    tree1.build(1,1,n);
    tree2.build(1,1,n);
    for(int i=1;i<=m;i++){
        scanf("%d%d%d%d%d",&in1,&in2,&in3,&in4,&in5);
        addedge(in1,in2,in3,in4,in5);
    }
    Dijkstra();
    if(dis[n]==inf){cout<<"-1\n";return 0;}
    for(int i=n;i!=1;i=from[i])     
        if(i<=n) ans.push_back(i);
    ans.push_back(1);
    reverse(ans.begin(),ans.end());
    cout<<dis[n]<<'\n';
    cout<<ans.size()<<'\n';
    for(auto it:ans) cout<<it<<' ';
    return 0;
}