学不会的线性基
前言
最后一次“杭电杯”结束了捏,看到同级的另一个队哐哐过题,感觉自己好菜捏😔。“某天赋怪”一天切13个蓝题👍,我只能切几个水题🤡,人家活该优秀!!!听说有个线性基的有点板的题,所以我来学一下(绝对不是不想填为了填博弈论的坑开的图论的坑!!!)
线性基的概念
称线性空间 \(V\) 的一个极大线性无关组为 \(V\) 的一组 Hamel 基 或 线性基,简称 基。
规定线性空间 \(\{\theta\}\) 的基为空集。
另外,将 \(V\) 的 维数 记作 \(\dim V\), 定义为基的元素个数。
线性基的性质
(1)等价性。在原数组A上进行XOR计算,与在线性基上进行XOR运算结果相同。
(2)最小性。P是满足性质(1)的所有集合中元素个数最少的,且P中不同的组合,其XOR结果也不同(即,线性无关性)。
(3)线性基P中不存在XOR为0的子集,如果存在,则说明P中存在能由其他元素表示出来的元素,违背了性质(2)。
Q:能不能举个栗子🌰
A:当然啦,我们不妨设\(P_a \oplus P_b \oplus P_c \oplus P_x = 0\),那么有$ P_a \oplus P_b \oplus P_c = \oplus P_x $ ,则说明\(P_x\)能由\(P_a,P_b,P_c\)表示出来
(4)原序列中的任何数,都可以由线性基中的一些数XOR得到。
线性基的构造
基本原理
为了满足线性基的最小性,构造线性基P的规则是“P中每个元素的二进制的位数均不同”。
如果一个数的二进制位数为i,那么说明它的第i位一定是1,而在i后的位置上的值均为0,所以我们不妨从最高位开始,判断x的第i位上是否为1,如果为1的话,判断线性基数组中是否已经有这个长度的线性基,如果有则进行XOR运算,缩短长度继续按照上面的步骤进行处理
void insert(int x){ //判断x应该以怎样的形式加入线性基
for(int i = N ; i >= 0 ; i --){
if(x >> i == 1){
if(p[i] == 0){
p[i] = x;
return ;
}
else x ^= p[i];
}
}
zero = true;
}
高斯消元法求线性基
我们不防设集合\(A = { a_1 , a_2 , a_3 , ... , a_n }\),最大位数为m,求线性基 $P = {p_1 , P_2 , ... , P_k} $,其中P_1 > P_2 > ... > P_k。
我们不妨把A的每个数看作m位二进制数,写成一个n * m 的01矩阵,矩阵的第i行,从左到右依次是\(a_i\)的第m - 1,m - 2, ... ,0位。把这个矩阵看成系数矩阵,用高斯消元法,转化成简化阶梯矩阵,如
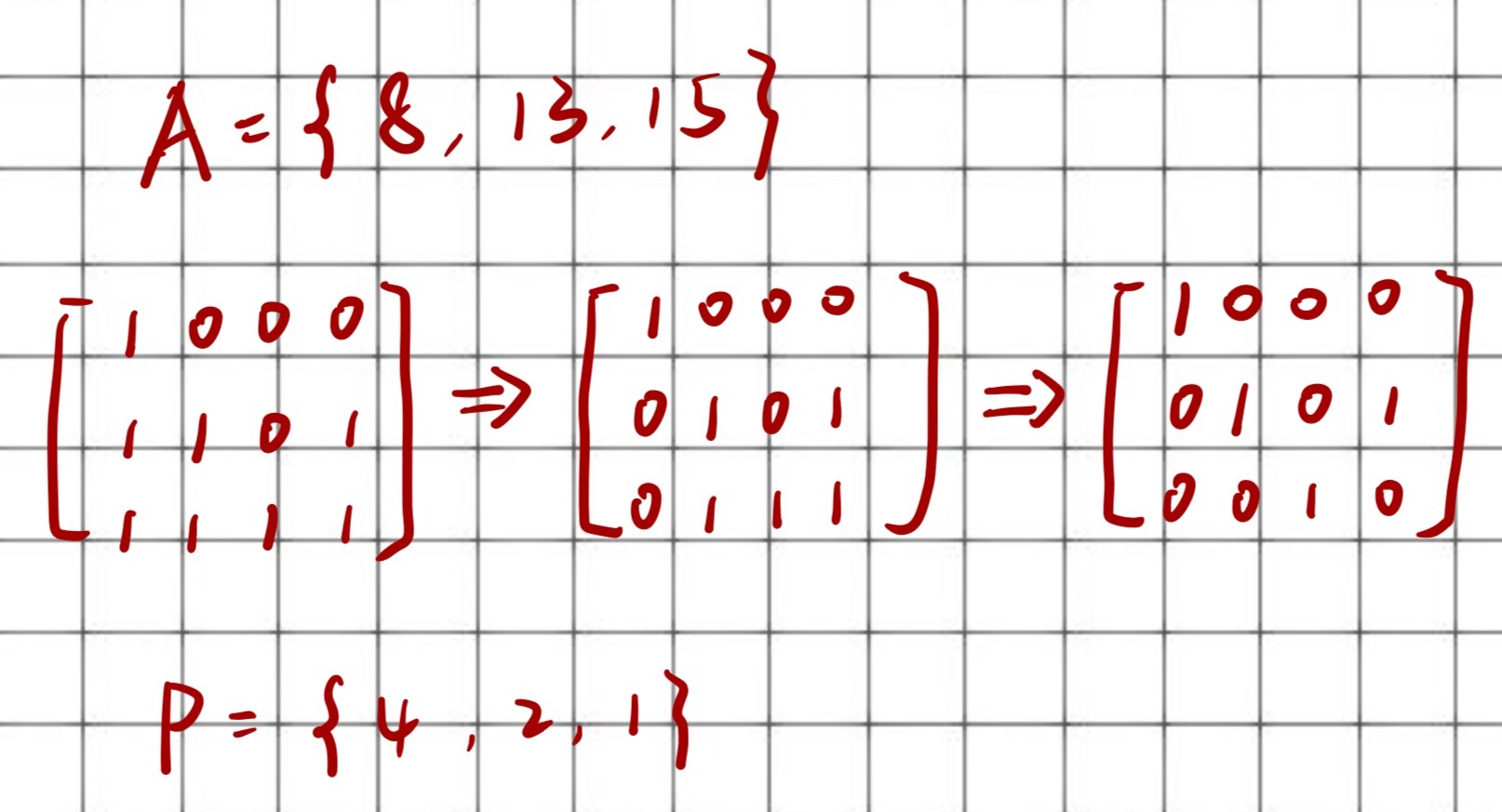
线性基的应用
最小异或和
由上面的高斯消元可知,如果简化行阶梯形中有全为0的行,说明A的最小异或和为0。除了0以外,A的最小异或和就是P的最小元素.因为P中的元素,经过高斯消元后形成的01矩阵中,代表某个元素的列最多只有一个1,这时,元素之间异或的结果必然增大。
最大异或和
要求线性基的最大异或和
1、未使用高斯消元法。利用贪心法,对每一个元素进行异或看是否会使值增大
2、使用高斯消元法。经过高斯消元后形成的01矩阵中,代表某个元素的列最多只有一个1,这时,元素之间异或的结果必然增大。
第k大异或和/第k小异或和
如果我们对线段基数组进行,高斯消元后会得到简化阶梯型的01矩阵,如图

我们不难发现:
最大异或和:异或所有元素
第二大异或和:异或前3个元素
...
第四大异或和:最后一个元素
【模板】线性基
题目背景
这是一道模板题。
题目描述
给定 \(n\) 个整数(数字可能重复),求在这些数中选取任意个,使得他们的异或和最大。
输入格式
第一行一个数 \(n\),表示元素个数
接下来一行 \(n\) 个数
输出格式
仅一行,表示答案。
样例 #1
样例输入 #1
2
1 1
样例输出 #1
1
提示
$ 1 \leq n \leq 50, 0 \leq S_i < 2 ^ {50} $
我的代码
/*
* 不带高斯消元
*/
#include <bits/stdc++.h>
#define int long long
const int N = 63;
int p[N];
void insert(int x){
for(int i = N ; i >= 0 ; i --){
if(x >> i == 1){
if(p[i] == 0){
p[i] = x;
return ;
}
else x ^= p[i];
}
}
}
int max(){
int ans = 0;
for(int i = N ; i >= 0 ; i --){
ans = std::max(ans,ans ^ p[i]);//逐个判断XOR上P[i],如果使ans更优,则XOR
}
return ans;
}
void solve() {
int n;
std::cin >> n;
for(int i = 1 ; i <= n ; i ++){
int t;
std::cin >> t;
insert(t);
}
std::cout << max() << "\n";
}
signed main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
int t = 1;
// std::cin >> t;
while (t--) {
solve();
}
return 0;
}
题目分析
题目已经说了这是一个模板题,只要按照上面的理论知识应该可以轻松写出代码吧。
XOR
Problem Description
XOR is a kind of bit operator, we define that as follow: for two binary base number A and B, let C=A XOR B, then for each bit of C, we can get its value by check the digit of corresponding position in A and B. And for each digit, 1 XOR 1 = 0, 1 XOR 0 = 1, 0 XOR 1 = 1, 0 XOR 0 = 0. And we simply write this operator as ^, like 3 ^ 1 = 2,4 ^ 3 = 7. XOR is an amazing operator and this is a question about XOR. We can choose several numbers and do XOR operatorion to them one by one, then we get another number. For example, if we choose 2,3 and 4, we can get 234=5. Now, you are given N numbers, and you can choose some of them(even a single number) to do XOR on them, and you can get many different numbers. Now I want you tell me which number is the K-th smallest number among them.
Input
First line of the input is a single integer T(T<=30), indicates there are T test cases.
For each test case, the first line is an integer N(1<=N<=10000), the number of numbers below. The second line contains N integers (each number is between 1 and 10^18). The third line is a number Q(1<=Q<=10000), the number of queries. The fourth line contains Q numbers(each number is between 1 and 10^18) K1,K2,......KQ.
Output
For each test case,first output Case #C: in a single line,C means the number of the test case which is from 1 to T. Then for each query, you should output a single line contains the Ki-th smallest number in them, if there are less than Ki different numbers, output -1.
Sample Input
2
2
1 2
4
1 2 3 4
3
1 2 3
5
1 2 3 4 5
Sample Output
Case #1:
1
2
3
-1
Case #2:
0
1
2
3
-1
Hint
If you choose a single number, the result you get is the number you choose.
Using long long instead of int because of the result may exceed 2^31-1.
Author
elfness
我的代码
#include <bits/stdc++.h>
#define int long long
const int N = 1e4 + 5;
int a[N];
int n;
bool zero;
void Gauss(){
int k = 1;
for(int j = (int) 1 << 62 ; j ; j >>= 1){
int i;
for(i = k;i <= n;i ++){//找到第j位为1的a[i]
if(a[i] & j) break;
}
if(i > n) continue;//没有找这样的a[i]
std::swap(a[i],a[k]);//把第k次找到的a[i]放到第k个位置
for(i = 1;i <= n ;i ++){//对每一个元素进行高斯消元
if(i != k && a[i] & j) a[i] ^= a[k];
}
k ++;//处理下一个位置
}
k --;//最后一次没有处理就跳出了
if(k != n) zero = true;//根据简化阶梯型的性质可以知道,k < n时说明有元素一行全是0
else zero = false;
n = k;//有k个元素
}
int query(int k){
int ans = 0;
if(zero) k--;
if(!k) return 0;
for(int i = n; i ;i --){
if(k & 1) ans ^= a[i];
k >>= 1;
}
if(k) return -1;
return ans;
}
void solve() {
std::cin >> n;
for(int i = 1;i <= n;i ++){
std::cin >> a[i];
}
Gauss();
int q;
std::cin >> q;
while (q --){
int k;
std::cin >> k;
std::cout << query(k) << "\n";
}
}
signed main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
int t = 1;
std::cin >> t;
for(int i = 1;i <= t;i ++) {
std::cout << "Case #" << i << ":\n";
solve();
}
return 0;
}