Alex_Wei的《图论基础》注

adolf-stalin / 2023-08-16 / 原文

0x00 拓扑排序与无向图DFS树
- 0x01 拓扑排序及其应用
- 无向图DFS树
0x10 最短路及其应用
- 0x11 相关定义
- 0x12 单源最短路
  - 0x120 Dijkstra
  - 0x121 SPFA与负环
  - 0x123 三角不等式
- 0x13 差分约束系统
  - 0x131 差分约束
  - 0x132 解的字典序极值
0x14 全源最短路
- 0x141 Johnson算法
- 0x142 Floyd与传递闭包
- 0x15 拓展问题
  - 0x151 最短路树
  - 0x152 删除边最短路
  - 0x153 平面图最小割【咕咕咕】
  - 0x154 k短路
  - 0x155 同余最短路
- 0x16 例题
0x20 无向图最小生成树
- 0x21 相关定义
- 0x22 最小生成树问题
  - 0x221 kruskal
  - 0x222 Boruvka算法
- 0x23 拟阵和生成树
  - 0x231 拟阵的定义和性质
  - 0x232 拟阵上的最优化问题
  - 0x233 最小生成树的性质
- 0x24 拓展问题
  - 0x241 次小生成树
  - 0x242 k小生成树
  - 0x243 最小生成树计数
  - 0x244 最小度限制生成树
- 0x25 例题
  - 0x251 P1967 [NOIP2013 提高组] 货车运输
  - 0x252 P4180 [BJWC2010] 严格次小生成树
  - 0x253 P4208 [JSOI2008] 最小生成树计数
  - 0x254 P5633 最小度限制生成树
  - 0x255 CF888G Xor-MST
  - 0x256 CF1305G Kuroni and Antihype
0x30 无向图连通性：双连通分量
- 0x31 相关定义
- 0x32 双连通的基本性质
  - 0x321 边双连通
  - 0x322 点双连通
  - 0x323 门杰定理及其推论
  - 0x324 双连通总结
  - 0x325 点双连通的更多性质
- 0x33 Tarjan 求割点
  - 0x331 非根的节点判定
  - 0x332 根的割点判定与代码
- 0x34 割边的求法
  - 0x341 Tarjan
  - 0x342 树上差分法
- 0x35 边双连通分量缩点
- 0x36 例题
  - 0x361 P3469 [POI2008] BLO-Blockade
  - 0x362 P2860 [USACO06JAN] Redundant Paths G
  - 0x363 CF51F Caterpillar
0x40 有向图可达：强连通分量
- 0x41 相关定义
- 0x42 有向图DFS树
- 0x43 Tarjan求SCC
- 0x44 Kosaraju算法
- 0x45 例题
  - 0x451 P3436 [POI2006] PRO-Professor Szu
  - 0x452 P7737 [NOI2021] 庆典
  - 0x453 AT_arc092_d [ARC092F] Two Faced Edges
0x50 欧拉回路
- 0x51 相关定义
- 0x52 欧拉路的判定
  - 0x521 有向图
  - 0x522 无向图
  - 0x523 混合图
- 0x53 Hierholzer 算法
- 0x54 例题
  - 0x541 P2731 [USACO3.3] 骑马修栅栏 Riding the Fences
  - 0x542 P1127 词链
  - 0x543 P3520 [POI2011] SMI-Garbage
  - 0x544 P3443 [POI2006] LIS-The Postman
  - 0x545 P3511 [POI2010] MOS-Bridges
  - 0x546 CF1361C Johnny and Megan's Necklace
  - 0x547 CF1458D Flip and Reverse

原文链接

0x00 拓扑排序与无向图DFS树

0x01 拓扑排序及其应用

首先是模板：

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std ;

const int MAXN = 105 ;

int degree[MAXN] ,n ;

struct Edge{
	int to ,next ;
}edge[MAXN<<1] ;
int head[MAXN] ,edge_cnt ;
inline void edge_add(int from , int to){
	edge[++edge_cnt].to = to ;
	edge[edge_cnt].next = head[from] ;
	head[from] = edge_cnt ;
}

queue<int> q ;

int main(){
	cin >> n ;
	for(int i = 1;i <= n;++i){
		int id ;cin >> id ;
		while(id){
			degree[id]++ ;
			edge_add(i , id) ;
			cin >> id ;
		}
	}
	for(int i = 1;i <= n;++i)	if(degree[i] == 0)	q.push(i) ;
	while(!q.empty()){
		int node = q.front() ;q.pop() ;
		cout << node << ' ' ;
		for(int i = head[node];i;i = edge[i].next){
			degree[edge[i].to]-- ;
			if(degree[edge[i].to] == 0)	q.push(edge[i].to) ;
		}
	}
	return 0 ;
}

然后是拓扑排序最关键的拓展应用。
$\centerdot$拓扑序DP。
$\centerdot$最小/最大字典序拓扑序。
$\centerdot$树拓扑序计数，拓扑序容斥。
$\centerdot$结合强连通分量、缩点解决图上问题。

无向图DFS树

之前碰到过这种题，感觉有点偏思维。关键就是树的DFS序，好像还可以求LCA。

0x10 最短路及其应用

0x11 相关定义

0x12 单源最短路

0x120 Dijkstra

贪心，适用于非负边权图。时间复杂度$O(m \log m)$。当图为稠密图($m=n^2$)时候退化为$O(n^2)$

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std ;
#define pii pair<int,int>
const int MAXN = 1e4+10 ;
const int MAXM = 5e5+10 ;

struct Edge{
	int next ,to ,w ;
}edge[MAXM] ;
int head[MAXN] ,edge_cnt ;

inline void edge_add(int from , int to , int w){
	edge[++edge_cnt].to = to ;
	edge[edge_cnt].next = head[from] ;
	edge[edge_cnt].w = w ;
	head[from] = edge_cnt ;
}

int dis[MAXN] ,vis[MAXN] ;
priority_queue<pii> q ;//先枚举小的 

inline void dij(int s){
	memset(dis , 0x7f , sizeof dis) ;
	dis[s] = 0 ;
	q.push(make_pair(0 , s)) ;
	while(q.empty() == 0){
		int node = q.top().second ;q.pop() ;
		vis[node] = false ;
		for(int i = head[node];i;i = edge[i].next){
			int v = edge[i].to ,w = edge[i].w ;
			if(dis[v] > dis[node] + w){
				dis[v] = dis[node] + w ;
				if(vis[v] == 0)	q.push(make_pair(-dis[v] , v)) ,vis[v] = true ;
			}
		}
	}
}

int main(){
	int n ,m ,s ;cin >> n >> m >> s ;
	for(int i = 1;i <= m;++i){
		int u ,v ,w ;cin >> u >> v >> w ;
		edge_add(u , v , w) ;
	}
	dij(s) ;
	for(int i = 1;i <= n;++i)	cout << dis[i] << ' ' ;
	return 0 ;
}

0x121 SPFA与负环

普通SPFA:

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std ;

const int MAXN = 1e4+10 ;
const int MAXM = 5e5+10 ;

struct Edge{
	int to ,next ,w ;
}edge[MAXM] ;
int head[MAXN] ,edge_cnt ;

inline void edge_add(int from , int to , int w){
	edge[++edge_cnt].next = head[from] ;
	edge[edge_cnt].to = to ;
	edge[edge_cnt].w = w ;
	head[from] = edge_cnt ;
}

bool vis[MAXN] ;
int dis[MAXN] ;
queue<int>	q ;

inline void spfa(int s){
	memset(dis , 0x7f , sizeof dis) ;
	q.push(s) ;
	dis[s] = 0 ;
	vis[s] = 1 ;
	while(!q.empty()){
		int node = q.front() ;
		q.pop() ;
		vis[node] = 0 ;
		for(int i = head[node];i;i = edge[i].next){
			int v = edge[i].to ,w = edge[i].w ;
			if(dis[v] > dis[node] + w){
                dis[v] = dis[node] + w ;
			    if(vis[v] == 0)	q.push(v) ,vis[v] = 1 ;
            }
		}
	}
}

int main(){
	int n ,m ,s ;
	cin >> n >> m >> s ;
	for(int i = 1;i <= m;++i){
		int u ,v ,w ;cin >> u >> v >> w ;
		edge_add(u , v , w) ;
	}
	spfa(s) ;
	for(int i = 1;i <= n;++i)	cout << dis[i] << ' ' ;
	return 0 ;
}

判断负环版SPFA:

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std ;

const int MAXN = 1e4+10 ;
const int MAXM = 5e5+10 ;

struct Edge{
	int to ,next ,w ;
}edge[MAXM<<1] ;
int head[MAXN] ,edge_cnt ;

inline void edge_add(int from , int to , int w){
	edge[++edge_cnt].next = head[from] ;
	edge[edge_cnt].to = to ;
	edge[edge_cnt].w = w ;
	head[from] = edge_cnt ;
}

bool vis[MAXN] ;
int dis[MAXN] ;
int len[MAXN] ;
queue<int>	q ;
int n ,m ;

inline void spfa(int s){
	memset(dis , 0x7f , sizeof dis) ;
	memset(vis , 0 , sizeof vis) ;
	memset(len , 0 , sizeof len) ;
	q.push(s) ;
	dis[s] = 0 ;
	vis[s] = 1 ;
	len[s] = 0 ;
	while(!q.empty()){
		int node = q.front() ;
		q.pop() ;
		vis[node] = 0 ;
		for(int i = head[node];i;i = edge[i].next){
			int v = edge[i].to ,w = edge[i].w ;
			if(dis[v] > dis[node] + w){
                dis[v] = dis[node] + w ;
                len[v] = len[node] + 1 ;
                if(len[v] == n){
                	printf("YES\n") ;
                	return ;
				}
			    if(vis[v] == 0)	q.push(v) ,vis[v] = 1 ;
            }
		}
	}
	cout << "NO\n" ;
}

inline void solve(){
	cin >> n >> m ;
	
	memset(head , 0 , sizeof head) ;
	edge_cnt = 0 ;
	
	for(int i = 1;i <= m;++i){
		int u ,v ,w ;cin >> u >> v >> w ;
		edge_add(u , v , w) ;
		if(w >= 0)	edge_add(v , u , w) ;
	}
	spfa(1) ;
}

int main(){
	int t ;cin >> t ;
	while(t--)	solve() ;
	return 0 ;
}

0x123 三角不等式

没啥说的。

0x13 差分约束系统

0x131 差分约束

注意在移项后新建边(v,u,w)。

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std ;

const int MAXN = 5e3+10 ;

struct Edge{
	int to ,next ,w ;
}edge[MAXN << 1] ;
int head[MAXN] ,edge_cnt ;

int n ,m ;

inline void edge_add(int from , int to , int w){
	edge[++edge_cnt].to = to ;
	edge[edge_cnt].next = head[from] ;
	edge[edge_cnt].w = w ;
	head[from] = edge_cnt ;
}

int dis[MAXN] ,vis[MAXN] ,len[MAXN] ;
queue<int> q ;
inline void spfa(int s){
	for(int i = 1;i <= n;++i)	q.push(i) ,vis[i] = 1 ;
	while(!q.empty()){
		int node = q.front() ;q.pop() ;
		vis[node] = 0 ;
		for(int i = head[node];i;i = edge[i].next){
			int v = edge[i].to ,w = edge[i].w ;
			if(dis[v] > dis[node] + w){
				dis[v] = dis[node] + w ;
				len[v] = len[node] + 1 ;
				if(len[v] == n){
					cout << "NO" ;
					return ;
				}
				if(vis[v] == 0){
					vis[v] = 1 ;
					q.push(v) ;
				}
			}
		}
	}
	for(int i = 1;i <= n;++i)
		cout << dis[i] << ' ' ;
}

int main(){
	cin >> n >> m ;
	for(int i = 1;i <= m;++i){
		int u ,v ,w ;cin >> u >> v >> w ;
		edge_add(v , u , w) ; 
	}
	spfa(1) ;
	return 0 ;
}

0x132 解的字典序极值

首先对“字典序极值”做出解释：应该是最大/小解的意思。
针对于$x_i$有边界的情况，以$x_i\leqslant0$为例：
将式子转化为：

\[(x_0 = 0)+0\geqslant x_i \]

那么我们只需要建立一个超级源点（$x_0$）并与之连接权值为0的边就可以满足最大的限制条件。
考虑我们的目的就是找出差分约束的最大解问题。
而此时我们发现，上面的差分约束的SPFA算法中将所有点直接入队的操作恰好等价于建立超级源点的操作，这使得SPFA求差分约束直接就可以求出在小于0的情况下的最大解。
那最大解就是所有节点向超级汇点连边，再直接将边反向就可以，然后求最大解，最后取相反数。
模板题：

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std ;

const int MAXN = 5e3+10 ;

struct Edge{
	int to ,next ,w ;
}edge[MAXN << 1] ;
int head[MAXN] ,edge_cnt ;

int n ,m ;

inline void edge_add(int from , int to , int w){
	edge[++edge_cnt].to = to ;
	edge[edge_cnt].next = head[from] ;
	edge[edge_cnt].w = w ;
	head[from] = edge_cnt ;
}

int dis[MAXN] ,vis[MAXN] ,len[MAXN] ;
queue<int> q ;
inline void spfa(int s){
	for(int i = 1;i <= n;++i)	q.push(i) ,vis[i] = 1 ;
	while(!q.empty()){
		int node = q.front() ;q.pop() ;
		vis[node] = 0 ;
		for(int i = head[node];i;i = edge[i].next){
			int v = edge[i].to ,w = edge[i].w ;
			if(dis[v] > dis[node] + w){
				dis[v] = dis[node] + w ;
				len[v] = len[node] + 1 ;
				if(len[v] == n){
					cout << "NO" ;
					return ;
				}
				if(vis[v] == 0){
					vis[v] = 1 ;
					q.push(v) ;
				}
			}
		}
	}
	for(int i = 1;i <= n;++i)
		cout << -dis[i] << ' ' ;
}

int main(){
	cin >> n >> m ;
	for(int i = 1;i <= m;++i){
		int u ,v ,w ;cin >> u >> v >> w ;
		edge_add(u , v , w) ; 
	}
	for(int i = 1;i <= n;++i)
		edge_add(0 , i , 0) ;
	spfa(1) ;
	return 0 ;
}

0x14 全源最短路

0x141 Johnson算法

注意几个点：

SPFA的松弛操作必然会在n-1轮后结束。
Dij的最短路松弛操作必须带h[u]-h[v]计算，其意义为：
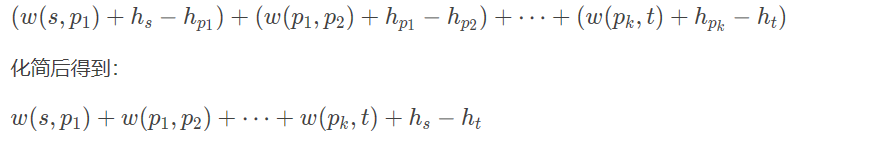
卡n次SPFA。
相较于n次Dij，Johnson接受负边权。
时间复杂度为$O(nm\log m)$。

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std ;

const int MAXN = 6e3+10 ;
#define ll long long
#define pii pair<int,int>
int n ,m ,h[MAXN] ,dis[MAXN] ;

struct Edge{
	int to ,next ,w ;
}edge[MAXN] ;
int head[MAXN] ,edge_cnt ;

inline void edge_add(int from , int to , int w){
	edge[++edge_cnt].to = to ;
	edge[edge_cnt].next = head[from] ;
	edge[edge_cnt].w = w ;
	head[from] = edge_cnt ;
}

bool vis[MAXN] ;
int main(){
	cin >> n >> m ;
	for(int i = 1;i <= m;++i){
		int u ,v ,w ;cin >> u >> v >> w ;
		edge_add(u , v , w) ;
	}
	
	for(int i = 1;i <= n;++i){
		bool flag = 0 ;
		for(int k = 1;k <= n;++k)
			for(int j = head[k];j;j = edge[j].next){
				int v = edge[j].to ,w = edge[j].w ;
				if(h[k] + w < h[v]){
					flag = 1 ;
					h[v] = h[k] + w ;
				}
			}
		if(i == n && flag){//截至到n还在更新 说明有负环！ 
			cout << -1 ;
			return 0 ; 
		}
	}
	
	for(int i = 1;i <= n;++i){
		ll ans = 0 ;
		for(int j = 1;j <= n;++j)	dis[j] = i == j ? 0 : 1e9 ;
		priority_queue<pii>	q ;
		q.push(make_pair(0 , i)) ;
		while(!q.empty()){
			int node = q.top().second ;
			q.pop() ;
			vis[node] = 0 ;
			for(int k = head[node];k;k = edge[k].next){
				int v = edge[k].to ,w = edge[k].w ;
				if(dis[v] > dis[node] + w + h[node] - h[v]){
					dis[v] = dis[node] + w + h[node] - h[v] ;
					if(vis[v] == 0)	q.push(make_pair(-dis[v] , v)) ,vis[v] = 1 ;
				}
			}
		}
		for(int j = 1;j <= n;++j)	ans += 1ll * j  * (dis[j] + (dis[j] < 1e9 ? h[j] - h[i] : 0)) ;
		cout << ans << '\n' ;
	}
	
	return 0 ;
}

0x142 Floyd与传递闭包

首先挂上Floyd板子：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std ;

const int MAXN = 1e3+10 ;
const int MAXM = 4510 ;

int f[MAXN][MAXN] ;
int n ,m ;
//0x7f7f7f7f = 1061109567 不支持加（超过int） 
int main(){
	cin >> n >> m ;
	memset(f , 0x3f , sizeof f) ;
	for(int i = 1;i <= n;++i)	f[i][i] = 0 ;
	for(int i = 1;i <= m;++i){
		int u ,v ,w ;cin >> u >> v >> w ;
		f[u][v] = f[v][u] = min(f[u][v] , w) ;
	}
	for(int k = 1;k <= n;++k){
		for(int i = 1;i <= n;++i){
			for(int j = 1;j <= n;++j){
				if(f[i][j] > f[i][k] + f[k][j])
					f[i][j] = f[i][k] + f[k][j] ;
			}
		}
	}
	for(int i = 1;i <= n;++i){
		for(int j = 1;j <= n;++j)	cout << f[i][j] << ' ' ;
		cout << '\n' ;
	}
	return 0 ;
}

再注意几个问题：

先枚举中间节点：因为只有已知的点才支持松弛操作

不经过编号大于 k的最短路已经考虑过了，而不经过编号大于 k+1的最短路相较于前者，只多出经过 k+1的路径——Alex_Wei

0x7f7f7f7f 不支持相加操作
注意重边
稠密图上效率高于Johnson
传递闭包有点sb。
将转移时的操作替换为：

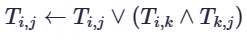
上三角逻辑与，下三角逻辑或。
没啥别的。

0x15 拓展问题

0x151 最短路树

将单源最短路中所有路径加成一棵树。
松弛的时候fa[j]=i即可。
如果将边反转，就是到达s的最短路树。
注意，以上操作仅限于无向图。有向图不一定。
拓展的最短路DAG很有趣。
任意一颗生成树都是最短路树（求解有向图最短路树？）
矩阵树定理可以辅助求解DAG生成树计数问题。
注意：最短路树建立fa关系的时候必须要和边的编号作联系否则重边就会GG!

0x152 删除边最短路

感觉对于最基础的删边最短路介绍可以看这里
针对区间取$\min$操作可以用线段树+LCA维护。
时间复杂度$\Theta(m\log n)$。
拓展1： 没设说的。感觉就是换了种定义方式。
拓展2： 小贪心，~~感性理解。~~

0x153 平面图最小割【咕咕咕】

学完网络流再来/kk

0x154 k短路

一个解决问题的有效思路是：找一种好的方式刻画研究对象，这里 “好的” 指便于考虑和解题。——Alex_Wei

由于这是在有向图上跑Dij,我们需要建立反向图以求得到达t的最短路树
感性理解，这个k短路一定是基于最短路情况下，在从s到t的所有祖先边中用一条非树边替换掉。这里需要根据$\delta(u,v)$排序找到最小可替换的后继，然后替换掉。没有后继就意味着这条边无法被替换掉，忽略。
那为什么一个序列至多只会有两条后继？因为序列是不停在变的，魏老师的意思是在一次序列变换中最多会产生2个后继，也就是下面的两种情况。
有图的blog
画画图更好理解。
网上偶然看到的，还没看\kk

0x155 同余最短路

具体请看专题与注。

0x16 例题

P1462 通往奥格瑞玛的道路
最大化最小值，用二分答案枚举并用dij判断是否合法。

#include <bits/stdc++.h>
using namespace std ;
#define ll long long
#define pii pair<int,int>
const int N = 1e4 + 5;

int n, m, b, f[N], dis[N];
vector<pii> e[N];
bool check(int x) {
  memset(dis, 0x3f, sizeof(dis));
  priority_queue<pii, vector<pii>, greater<pii>> q;
  q.push({dis[1] = 0, 1});
  while(!q.empty()) {
    pii t = q.top(); q.pop();
    int id = t.second;
    if(dis[id] != t.first) continue;
    for(auto _ : e[id]) {
      int it = _.first, v = dis[id] + _.second;
      if(f[it] <= x && v < dis[it]) q.push({dis[it] = v, it});
    }
  }
  return dis[n] <= b;
}

int main() {
  cin >> n >> m >> b;
  for(int i = 1; i <= n; i++) cin >> f[i];
  for(int i = 1; i <= m; i++) {
    int a, b, c;
    cin >> a >> b >> c;
    e[a].push_back({b, c});
    e[b].push_back({a, c});
  }
  if(!check(1e9)) cout << "AFK\n", exit(0);
  int l = f[1], r = 1e9;
  while(l < r) {
    int m = l + r >> 1;
    if(check(m)) r = m;
    else l = m + 1;
  }
  cout << l << "\n";
  return 0;
}

P4568 [JLOI2011] 飞行路线
分层图板子。特点:k很小，可以枚举作为层数

#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=2e5+100;
typedef long long LL;
typedef pair<LL,LL>P;///first最短距离,second顶点的编号 
struct edge{
	LL to,cost;
};
vector<edge>g[maxn];
LL vis[maxn];
LL dis[maxn];
LL n,m,k,start,final;
void dijkstra()
{
	LL s=start;///起点是start
	memset(dis,0x3f,sizeof(dis));///初始化 
	dis[s]=0;
	memset(vis,0,sizeof(vis));///初始化 
	priority_queue< P, vector<P> , greater<P> >que;
	que.push({0,s});
	while(!que.empty())
	{
		P p=que.top();que.pop();
		int v=p.second;
		if(vis[v]) continue;
		vis[v]=1;
		for(int i=0;i<g[v].size();i++)
		{
			edge e=g[v][i];
			if(dis[e.to]>dis[v]+e.cost)
			{
				dis[e.to]=dis[v]+e.cost;
				que.push({dis[e.to],e.to});	
			}	
		}	
	}
}
int main(void)
{
  cin.tie(0);std::ios::sync_with_stdio(false);
  cin>>n>>m>>k;
  cin>>start>>final;
  while(m--){
  	 LL x,y,c;cin>>x>>y>>c;
  	 //第0层
	 g[x].push_back({y,c});g[y].push_back({x,c}); 
  	 for(LL j=1;j<=k;j++){//1~k层 
  	 	g[x+(j-1)*n].push_back({y+j*n,0});
		g[y+(j-1)*n].push_back({x+j*n,0});   
		g[x+j*n].push_back({y+j*n,c});
		g[y+j*n].push_back({x+j*n,c});	
	 }
  }
  for(LL j=1;j<=k;j++){//可能k>n,也就是终点不一定是k*n+t ，可能不需要走到第k层图 
  	g[final+(j-1)*n].push_back({final+j*n,0});
  }
  dijkstra();
  cout<<dis[final+k*n]<<endl;
return 0;
}

P6880 [JOI 2020 Final] オリンピックバス
最短路树的思维题，比较常规。有更详细的blog
P4926 [1007] 倍杀测量者
关于log2可以使得乘法转换成加法操作没想到。。。
二分答案没想到（最大化t）
P5304 [GXOI/GZOI2019] 旅行者
dij求多源最短路问题，考虑使用二进制分组。
注意还要建反图，因为单向路的情况，两端交换可能答案不同。
P5590 赛车游戏
很妙的转化！区间性质的取值范围题可以分别将上下界转化为最短路差分约束问题。
有几个坑点：
一、对于不在1~n之间通路上的边不要加入，会对操作产生影响。
二、在判断是否为路径时的inroad不要被覆盖！

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std ;

#define pii pair<int,int>
const int MAXM = 2e3+10 ;
const int MAXN = 1e3+10 ;

int n ,m ;

struct Edge{
	int to ,next ,w ;
}edge[MAXM<<1] ;
int head[MAXN] ,edge_cnt ;

inline void edge_add(int from , int to , int w){
	edge[++edge_cnt].to = to ;
	edge[edge_cnt].next = head[from] ;
	edge[edge_cnt].w = w ;
	head[from] = edge_cnt ;
}

struct G{
	int to ,next ;
}g[MAXM<<1] ;
int gh[MAXN] ,g_cnt ;
inline void g_add(int from , int to){
	g[++g_cnt].to = to ;
	g[g_cnt].next = gh[from] ;
	gh[from] = g_cnt ;
}

bool touch[MAXN] ;
bool inroad[MAXN] ;
inline void dfs(int node){
	touch[node] = 1 ;
	for(int i = gh[node];i;i = g[i].next){
		if(!touch[g[i].to])	dfs(g[i].to) ;
		inroad[node] = (inroad[g[i].to] || inroad[node]) ; 
	}
}

int dis[MAXN] ,len[MAXN] ;
bool vis[MAXN] ;
queue<int>	q ;
int u[MAXM] ,v[MAXM] ;
inline void spfa(int s){
	memset(dis , 0x7f , sizeof dis) ;dis[s] = 0 ;
	q.push(s) ;
	while(!q.empty()){
		int node = q.front() ;
		q.pop() ;
		vis[node] = 0 ;
		for(int i = head[node];i;i = edge[i].next){
			int vv = edge[i].to ,w = edge[i].w ;
			if(dis[vv] > dis[node] + w){
				dis[vv] = dis[node] + w ;
				len[vv] = len[node] + 1 ;
				if(len[vv] == n){
					cout << -1 ;
					return ;
				}
				if(vis[vv] == 0){
					q.push(vv) ;
					vis[vv] = 1 ;
				}
			}
		}
	}
	
	cout << n << ' ' << m << '\n' ;
	for(int i = 1;i <= m;++i){
		int w = dis[v[i]] - dis[u[i]] ;
		if(!inroad[u[i]] || !inroad[v[i]])	w = 1 ;
		cout << u[i] << ' ' << v[i] << ' ' << w << '\n' ;
	}
}

int main(){
	cin >> n >> m ;
	for(int i = 1;i <= m;++i){
		cin >> u[i] >> v[i] ;
		g_add(u[i] , v[i]) ;
	}
	inroad[n] = 1 ;
	dfs(1) ;
	if(inroad[1] == 0){
		cout << -1 ;
		return 0 ;
	}
	for(int i = 1;i <= m;++i){
		if(!inroad[u[i]] || !inroad[v[i]])	continue ;
		edge_add(u[i] , v[i] , 9) ;
		edge_add(v[i] , u[i] , -1) ;
	}
	spfa(1) ;
	return 0 ;
}

P3573 [POI2014] RAJ-Rally
不是魏老师这道题不可以用删边最短路做吧/kk 有向图咋用删边做捏
看到有向无环图，可以使用拓扑排序。
枚举每个点的链接情况，从一个集合中加入到另一个集合中去。
维护集合操作可以使用multiset，附带取最值功能。

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<set>
#include<climits>
using namespace std ;

const int MAXN = 5e5+10 ;
const int MAXM = 1e6+10 ;

int n ,m ,ans = INT_MAX ,anspos ;
int dt[MAXN] ,ds[MAXN] ,topo[MAXN] ,cnt ,deg1[MAXN] ,deg2[MAXN] ;
struct Edge{
	int to ,next ;
}edge1[MAXM] ,edge2[MAXM] ;
int head1[MAXN] ,head2[MAXN] ,edge_cnt1 ,edge_cnt2 ;

inline void edge_add1(int from , int to){
	edge1[++edge_cnt1].to = to ;
	edge1[edge_cnt1].next = head1[from] ;
	head1[from] = edge_cnt1 ;
}

inline void edge_add2(int from , int to){
	edge2[++edge_cnt2].to = to ;
	edge2[edge_cnt2].next = head2[from] ;
	head2[from] = edge_cnt2 ;
}

queue<int> q ;

inline void topo1(){
	for(int i = 1;i <= n;++i)	if(!deg1[i])	q.push(i) ,topo[++cnt] = i ;
	while(!q.empty()){
		int u = q.front() ;q.pop() ;
		for(int i = head1[u];i;i = edge1[i].next){
			int v = edge1[i].to ;
			dt[v] = max(dt[v] , dt[u] + 1) ;
			deg1[v]-- ;
			if(!deg1[v])	q.push(v) ,topo[++cnt] = v ;
		}
	}
}

inline void topo2(){
	for(int i = 1;i <= n;++i)	if(!deg2[i])	q.push(i) ;
	while(!q.empty()){
		int u = q.front() ;q.pop() ;
		for(int i = head2[u];i;i = edge2[i].next){
			int v = edge2[i].to ;
			ds[v] = max(ds[v] , ds[u] + 1) ;
			deg2[v]-- ;
			if(!deg2[v])	q.push(v) ;
		}
	}
}

multiset<int>	s ;

int main(){
	cin >> n >> m ;
	for(int i = 1;i <= m;++i){
		int u ,v ;cin >> u >> v ;
		edge_add1(u , v) ;deg1[v]++ ;
		edge_add2(v , u) ;deg2[u]++ ;//反向图：便于构建ds数组 
	}
	topo1() ;
	topo2() ;
	for(int i = 1;i <= n;++i)	s.insert(ds[i]) ;
	for(int i = 1;i <= n;++i){
		int u = topo[i] ;
		s.erase(s.find(ds[u])) ;
		for(int j = head2[u];j;j = edge2[j].next){//在反图中删去 
			int v = edge2[j].to ;
			s.erase(s.find(dt[v] + 1 + ds[u])) ;
		}
		if(*(--s.end()) < ans){
			ans = *(--s.end()) ;
			anspos = u ;
		}
		s.insert(dt[u]) ;
		for(int j = head1[u];j;j = edge1[j].next){//在原图中添加 
			int v = edge1[j].to ;
			s.insert(dt[u] + 1 + ds[v]) ;
		}
	}
	cout << anspos << ' ' << ans ;
	return 0 ;
}

P4001 [ICPC-Beijing 2006] 狼抓兔子【咕咕咕】
学完网络流再来。
P7916 [CSP-S 2021] 交通规划【咕咕咕】
学完网络流再来。
CF1765I Infinite Chess
由于求解最小步数，所以考虑最短路。直接建图过于密集，可以考虑先离散化。由于行数很小，可以直接对行数进行枚举。
AT_arc084_b [ABC077D] Small Multiple
首先发现这道题是数可以是无限大的，甚至有可能会爆__int128
考虑不需要实际知道这个数就能得到答案的方法感觉很像数位DP?
由于位数不固定，猜测可以使用取模
分解为+1和$\times$10两种操作由于求最小数位累加和考虑可以直接最短路
证明出现的第一个较小解就是最小解：如果再进行+1操作数值只会越变越大。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std ;

const int MAXN = 1e5+10 ;

int k ,f[MAXN] ;
queue<int>	q ;

int main(){
	cin >> k ;
	memset(f , 0x3f , sizeof f) ;
	f[1] = 1 ;q.push(1) ;
	while(!q.empty()){
		int u = q.front() ;
		q.pop() ;
		int v = u * 10 % k ;//考虑*10：代价为0 
		//及时取模不影响结果是这道题解题关键！ 
		if(f[u] < f[v]){
			f[v] = f[u] ;
			if(!vis[v])	q.push(v) ;
		}
		v = (u + 1) % k ;//+1：代价+1 
		if(f[u] < f[v]){
			f[v] = f[u] + 1 ;
			if(!vis[v])	q.push(v) ;
		}
	}
	cout << f[0] ;//要求是k的倍数，由于对k取模了所以是0 
	return 0 ;
}

AT_agc056_c [AGC056C] 01 Balanced
首先考虑条件转化。$d_i$表示从1到i中0的个数减去1的个数。
思路很好想，关键在于求证以及对于01bfs的实现（代替dij）
注意MAXN<<1+MAXM<<1不知为何会RE要用3*MAXN(
由于最小化原串字典序，也就是让0尽可能多，$d_i$最大，所以使用最大值差分约束。
注意：当条件为绝对值时，我们需要建双向边！

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std ; 
#define ll long long
const int MAXN = 1e6+10 ;
const int MAXM = 2e5+10 ;

int n ,m ;

struct Edge{
	int to ,next ,w ;
}edge[MAXN*3] ;
int head[MAXN] ,edge_cnt ;

inline void edge_add(int from , int to , int w){
	edge[++edge_cnt].to = to ;
	edge[edge_cnt].w = w ;
	edge[edge_cnt].next = head[from] ;
	head[from] = edge_cnt ;
}

deque<int>	q ;
int dis[MAXN] ;

inline void bfs01(int s){
	memset(dis , 0x7f , sizeof dis) ;
	dis[0] = 0 ;q.push_back(0) ;
	while(!q.empty()){
		int u = q.front() ;
		q.pop_front() ;
		for(int i = head[u];i;i = edge[i].next){
			int v = edge[i].to ,w = edge[i].w ;
			if(dis[v] > dis[u] + w){
				dis[v] = dis[u] + w ;
				if(w)	q.push_back(v) ;
				else q.push_front(v) ;
			}
		}
	}
	for(int i = 1;i <= n;++i)	cout << (dis[i] == dis[i-1] ? 0 : 1) ;
}

int main(){
	cin >> n >> m ;
	for(int i = 1;i <= n;++i){
		edge_add(i-1 , i , 1) ;
		edge_add(i , i-1 , 1) ;
	}
	for(int i = 1;i <= m;++i){
		int l ,r ;cin >> l >> r ;
		edge_add(l-1 , r , 0) ;
		edge_add(r , l-1 , 0) ;
	}
	bfs01(0) ;
	return 0 ;
}

P7516 [省选联考 2021 A/B 卷] 图函数
遇事不决，先推性质。
解法一：floyd$\Theta(n^3)$

//O(n^3) 做法 
/*
首先推出几个关键性质：
1. 由于会删除节点 每个点对(i,j)有且仅会在最小编号的节点出贡献一次
2. 针对每组点对，都存在一个最小的节点编号，保证这组点对在大于最大值的h()中产生一次贡献
3. 那么我们只需要求出点对的最小节点编号最大即可。h()的贡献被均摊，也就是说h(i)可以有的贡献h(i+a)一定有。
求任意两点之间的最大最小编号，考虑Floyd。 
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std ;
#define ll long long
#define pii pair<int,int>
const int MAXN = 1e3+10 ;
const int MAXM = 2e5+10 ;

int n ,m ;
int dis[MAXN][MAXN] ,h[MAXM] ;

int main(){
	ios::sync_with_stdio(0) ,cin.tie(0) ,cout.tie(0) ;
	cin >> n >> m ;
	for(int i = 1;i <= n;++i)	dis[i][i] = m+1 ;//令dis[][]表示两个点对之间的最大的最小编号 
	//自环贡献是最大：默认对答案无影响 
	for(int i = 1;i <= m;++i){
		int u ,v ;cin >> u >> v ;
		dis[u][v] = i ;
	}
	for(int k = n;k >= 1;--k){
		for(int i = 1;i <= n;++i){
			if(dis[i][k] == 0)	continue ;
			int lim = i < k ? n : k-1 ;//剪枝 
			for(int j = 1;j <= lim;++j){
				dis[i][j] = max(dis[i][j] , min(dis[i][k] , dis[k][j])) ;//转移 
			}
		}
		for(int i = k;i <= n;++i){//枚举任何两个点的点对 
			int t = min(dis[i][k] , dis[k][i]) ;//取最小 
			if(t)	h[t-1]++ ;//两点之间可以相互达到 大于等于t都不可以。 
		}
	}
	for(int i = m;i >= 0;--i)	h[i] += h[i+1] ;//h[]具有分摊关系 向上取后缀和 
	for(int i = 0;i <= m;++i)	cout << h[i] << ' ' ;
	return 0 ;
}

解法二：反图+贪心+bfs$\Theta(nm)$

//O(NM)做法 
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std ;

const int MAXN = 1e3+10 ;
const int MAXM = 2e5+10 ;

int n ,m ;
struct Edge1{
	int to ,next ;
}edge1[MAXM] ,edge2[MAXM] ;
int head1[MAXN] ,edge_cnt1 ;
inline void edge_add1(int from , int to){
	edge1[++edge_cnt1].to = to ;
	edge1[edge_cnt1].next = head1[from] ;
	head1[from] = edge_cnt1 ;
}
int head2[MAXN] ,edge_cnt2 ;
inline void edge_add2(int from , int to){
	edge2[++edge_cnt2].to = to ;
	edge2[edge_cnt2].next = head2[from] ;
	head2[from] = edge_cnt2 ;
}

int u[MAXM] ,v[MAXM] ,h[MAXM] ;
int a[MAXN] ,b[MAXN] ;

int main(){
	ios::sync_with_stdio(0) ,cin.tie(0) ,cout.tie(0) ;
	cin >> n >> m ;
	h[m] = n ;//当删除所有边时，每个点都能做贡献
	for(int i = 1;i <= m;++i)	cin >> u[i] >> v[i] ;//边
	for(int i = n;i;--i){//枚举G(u) 
		memset(head1 , 0 , sizeof head1) ;
		memset(head2 , 0 , sizeof head2) ;
		edge_cnt1 = edge_cnt2 = 0 ;
		for(int j = i;j <= n;++j)	a[j] = b[j] = 0 ;
		a[i] = b[i] = 1 ;//存在贡献 
		for(int w = m;w;--w){//枚举边的编号 加入边
			if(u[w] < i || v[w] < i)	continue ;//编号小于i说明之前就会被删除
			if(!a[v[w]]){//v若可达 对连通性没有任何贡献 
				if(!a[u[w]])	edge_add1(u[w] , v[w]) ;//u也不可达 现在没用，但是先留着
				else{//bfs将经过的点标记为可达
					queue<int> q ;
					q.push(v[w]) ;
					h[w-1] += b[v[w]] ;
					a[v[w]] = 1 ;
					while(!q.empty()){
						int t = q.front() ;q.pop() ;
						for(int it = head1[t];it;it = edge1[it].next){
							if(!a[edge1[it].to])	q.push(edge1[it].to) ,h[w-1] += b[edge1[it].to] ,a[edge1[it].to] = 1 ;
						}
					}
				}
			}
			if(!b[u[w]]){//反图同理 保证互相可达 
				if(!b[v[w]])	edge_add2(v[w] , u[w]) ;
				else{
					queue<int> q ;
					q.push(u[w]) ;
					h[w-1] += a[u[w]] ;
					b[u[w]] = 1 ;
					while(!q.empty()){
						int t = q.front() ;q.pop() ;
						for(int it = head2[t];it;it = edge2[it].next){
							if(!b[edge2[it].to])	q.push(edge2[it].to) ,h[w-1] += a[edge2[it].to] ,b[edge2[it].to] = 1 ;
						}
					}
				}
			}
		}
	}
	for(int i = m;i >= 0;--i)	h[i] += h[i+1] ;
	for(int i = 0;i <= m;++i)	cout << h[i] << ' ' ;
	return 0 ;
}

解法三：bitset$\Theta(\frac{n^3}{\omega})$
针对枚举i的操作进行简化，批量解决i的枚举。
了解了bitset判断行条件的方式：先使用bitset划分区域之后使用两个函数_Find_first 和 _Find_next快速查找1的位置。

//O(n^3/w)做法 
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<bitset>
using namespace std ;
#define pii pair<int,int>
const int MAXN = 1e3+10 ;
const int MAXM = 2e5+10 ;
 
int n ,m ;
int h[MAXM] ,u[MAXM] ,v[MAXM] ;
bitset<MAXN> a[2][MAXN] ,r[2][MAXN] ,e[2][MAXN] ;
queue<pii>	q ;

inline void light(int x , int y , int w , int opt){
	h[w - 1] += a[opt ^ 1][x][y] ;//这个点有没有贡献还取决于反图有没有贡献 
    a[opt][x][y] = r[opt][y][x] = 1 ,q.push(make_pair(x , y)) ;//当前图肯定没有问题 
}

inline void add(int w , int opt , int u , int v){
	e[opt][u][v] = 1 ;
	bitset<MAXN> p = r[opt][u] & ~r[opt][v] ;//判断u是否能够到达v （批量计算） 
	for(int st = p._Find_first();st <= u && st < v;st = p._Find_next(st)){//找到第一个1，下一个1 
		light(st , v , w , opt) ;
    	while(!q.empty()){//计算当前点的贡献 
    		int i = q.front().first ,j = q.front().second ;
    		q.pop() ;
    		bitset<MAXN> nxt = e[opt][j] & ~a[opt][i] ;//更新i可达to的条件 
    		for(int to = nxt._Find_next(st);to < MAXN;to = nxt._Find_next(to)) light(i , to , w , opt) ;
    	}
	}
}

int main(){
	ios::sync_with_stdio(0) ,cin.tie(0) ,cout.tie(0) ;
	cin >> n >> m ;
	h[m] = n ;
	for(int i = 1;i <= n;++i)	a[0][i][1] = r[0][i][i] = a[1][i][i] = r[1][i][i] = 1 ;
	//初始化 自己肯定到自己 （0/1为正/反图）
	for(int i = 1;i <= m;++i)	cin >> u[i] >> v[i] ;
	for(int w = m;w;--w)	add(w , 0 , u[w] , v[w]) ,add(w , 1 , v[w] , u[w]) ;
	for(int i = m;i >= 0;--i)	h[i] += h[i+1] ;
	for(int i = 0;i <= m;++i)	cout << h[i] << ' ' ;
	return 0 ;
}

AT_arc092_d [ARC092F] Two Faced Edges
分讨一下，直接将两个性质推出来。针对后面的性质，将问题简化后发现使用dfs序就可以判断。方法有很多种。

你看它不用算具体的东西，只用算一个总和，这不用贡献法用什么？————zxy

P7515 [省选联考 2021 A 卷] 矩阵游戏
感觉不如zxy的题解。
首次接触调整法。一开始读题的时候甚至都没有发现这个$0\leqslant \pm r_i\pm c_j\pm a_{i,j}\leqslant10^6$条件的重要性。。。
将矩阵的关键变量放在最后一列、最后一行可能是更符合逻辑的（因为他是最底层，受变量的改变影响最少）
调整法，首先需要将最初合法的A矩阵构造出来，可以假设最后一行、最后1列全部为0.
接下来调整。调整一整行或一整列，同时在奇数项+1且偶数项-1不会使得B矩阵有任何改变。
这时假设$r_i$表示行调整值，$c_i$表示列调整值，这样就有了上面的式子。
这就是魏老师说的“三个元素”的由来。如何避免三个元素的高斯消元，从而避免多次分讨？
考虑将原图进行二染色，每种颜色对应一种等式。
注意，这里奇偶数和正负的划分没有联系，可以任选。
这种网格见图还要小心链式前向星可能会TLE，尽量使用vector。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
using namespace std ;
#define ll long long
#define pil pair<int,ll>
const int MAXN = 605 ;

int t ,n ,m ,len[MAXN] ,vis[MAXN] ;
ll dis[MAXN] ,a[MAXN][MAXN] ,b[MAXN][MAXN] ;
vector<pil>	g[MAXN] ;

inline void edge_add(int from , int to , ll w){
	g[from].push_back(make_pair(to , w)) ;
}

inline void spfa(){
	memset(dis , 0x3f , sizeof dis) ;
	memset(vis , 0 , sizeof vis) ;
	memset(len , 0 , sizeof len) ;
	queue<int>	q ;
	q.push(1) ;
	dis[1] = 0 ;
	while(!q.empty()){
		int u = q.front() ;q.pop() ;
		vis[u] = 0 ;
		for(int i = 0;i < g[u].size();++i){
			int v = g[u][i].first ;ll w = g[u][i].second ;
			if(dis[v] > dis[u] + w){
				dis[v] = dis[u] + w ;
				len[v] = len[u] + 1 ;
				if(len[v] >= n+m){
					cout << "NO\n" ;
					return ;
				}
				if(vis[v] == 0){
					q.push(v) ;
					vis[v] = 1 ;
				}
			}
		}
	}
	cout << "YES\n" ;
	for(int i = 1;i <= n;++i)
		for(int j = 1;j <= m;++j){
			if((i + j) % 2){
				cout << dis[i] - dis[j+n] + a[i][j] ;
			}else{
				cout << dis[j+n] - dis[i] + a[i][j] ;
			}
			cout << ' ' ;
			if(j == m)	cout << '\n' ;
		}
}

inline void solve(){
	memset(a , 0 , sizeof a) ;
	for(int i = 1;i <= n+m;++i)	g[i].clear() ;
	cin >> n >> m ;
	for(int i = 1;i < n;++i)	for(int j = 1;j < m;++j)	cin >> b[i][j] ;
	for(int i = n-1;i >= 1;--i)	for(int j = m-1;j >= 1;--j)	a[i][j] = b[i][j] - a[i+1][j] - a[i][j+1] - a[i+1][j+1] ;
	for(int i = 1;i <= n;++i)
		for(int j = 1;j <= m;++j){
			if((i+j) % 2){
				edge_add(i , j+n , a[i][j]) ;
				edge_add(j+n , i , 1e6-a[i][j]) ;
			}else{
				edge_add(j+n , i , a[i][j]) ;
				edge_add(i , j+n , 1e6-a[i][j]) ;
			}
		}
	spfa() ;
}

int main(){
	ios::sync_with_stdio(0) ,cin.tie(0) ,cout.tie(0) ;
	cin >> t ;
	while(t--)	solve() ;
	return 0 ;
}

CF1163F Indecisive Taxi Fee
脑子进水了。。。四种情况少了俩。。。~~这间接导致我压根没往删边最短路的方向想（（（~~
你说得对，但是魏老师的code好tm毒瘤啊\kk
不如看ycx巨佬的blog
注意静态线段树不如multiset差分。
P2685 [TJOI2012] 桥
删边最短路模板。
P2483 【模板】k 短路 / [SDOI2010] 魔法猪学院
模板题。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std ;
#define pid pair<int,double>
#define pdi pair<double,int>
const int MAXN = 2e5+10 ;
const int MAXM = 2e5+10 ;

int n ,m ;
double e ;
vector<int>	edge[MAXN] ,redge[MAXN] ;
int u[MAXM] ,v[MAXM] ;
double w[MAXM] ;

inline void init(){
	cin >> n >> m >> e ;
	for(int i = 1;i <= m;++i){
		cin >> u[i] >> v[i] >> w[i] ;
		edge[u[i]].push_back(i) ;
		redge[v[i]].push_back(i) ;
	}
}

int fa[MAXN] ,eid[MAXN] ,on[MAXN] ;//最短路树 边号 是否在树上 
vector<int>	g[MAXN] ;
double dis[MAXN] ;
bool vis[MAXN] ;

inline void dij(){
	for(int i = 1;i <= n;++i)	dis[i] = 1e9 ;
	priority_queue<pdi> q ;
	q.push(make_pair(0 , n)) ;dis[n] = 0 ;
	while(!q.empty()){
		int node = q.top().second ;q.pop() ;
		vis[node] = 0 ;
		for(int i = 0;i < redge[node].size();++i){
			int id = redge[node][i] ;
			if(dis[u[id]] > dis[v[id]] + w[id]){//因为是反边所以松弛操作也要相反。 
				fa[u[id]] = node ;
				eid[u[id]] = id ;//注意记录边的编号防止重边！ 
				dis[u[id]] = dis[v[id]] + w[id] ;
				if(vis[u[id]])	continue ;
				q.push(make_pair(-dis[u[id]] , u[id])) ;
				vis[u[id]] = 1 ;
			}
		}
	}
	for(int i = 1;i < n;++i)	on[eid[i]] = 1 ;//每一条边号都在树上，n号节点没有出边	
}

int cnt ;
int rt[MAXN] ,ls[MAXN<<5] ,rs[MAXN<<5] ;

inline void modify(int pre , int &x , int l , int r , int p){//单点增加 
	x = ++cnt ;//动态加点 
	ls[x] = ls[pre] ,rs[x] = rs[pre] ;//后来递归时更改 
	if(l == r)	return ;
	int mid = l + r >> 1 ;
	if(p <= mid)	modify(ls[pre] , ls[x] , l , mid , p) ;
	else modify(rs[pre] , rs[x] , mid+1 , r , p) ;
}

inline int binary(int l , int r , int p , int x){//单点查询位置 
	if(!x)	return -1 ;
	if(l == r)	return l ;
	int mid = l + r >> 1 ;
	if(p <= mid){
		int ret = binary(l , mid , p , ls[x]) ;
		if(ret != -1)	return ret ;
	}
	return binary(mid+1 , r , p , rs[x]) ;
}

struct schedule{
	double val ;//价值 
	int lstid ,curid ;//过去第几棵线段树，当前 
	bool operator < (const schedule &z)const{
		return val > z.val ;
	}
};

int pos[MAXM] ;

inline void dfs(int id){
	if(id != n)//添加所有出边 
		for(int i = 0;i < edge[id].size();++i){
			int num = edge[id][i] ;
			modify(rt[id] , rt[id] , 1 , m , pos[num]) ;
		}
	for(int i = 0;i < g[id].size();++i){//向上找祖先 
		int num = g[id][i] ;
		rt[num] = rt[id] ;
		dfs(num) ;
	}
}

pdi d[MAXM] ;
double len[MAXM] ;
inline void solve(){
	for(int i = 1;i <= m;++i){
		len[i] = dis[v[i]] - dis[u[i]] + w[i] ;//计算delta值 
		if(on[i])	len[i] = 1e9 ;//是最短路树上的边，delta为无穷大 
		d[i] = make_pair(len[i] , i) ;
	}
	sort(d+1 , d+1+m) ;//贪心 
	for(int i = 1;i <= m;++i)	pos[d[i].second] = i ;//边对应的边号 
	for(int i = 1;i < n;++i)	g[fa[i]].push_back(i) ;//建立最短路树 
	dfs(n) ;//建线段树 
	double dd = dis[1] ;
	int ans = 0 ;
	priority_queue<schedule>	q ;
	q.push({0,-1,0}) ;
	while(!q.empty()){
		schedule t = q.top() ;q.pop() ;
		if(e + 1e-9 < dd + t.val)	break ;//权值超过了 
		ans++ ;//第ans小 
		e -= dd + t.val ;//减去delta+基础长度 
		int ind = t.lstid == -1 ? 0 : t.lstid ? v[t.lstid] : 1 ;//可持久化找边 
    	if(rt[ind]){
    		int nxt = binary(1 , m , pos[t.curid] + 1 , rt[ind]) ;//权值最小的边 
    		if(nxt != -1) q.push({t.val - len[t.curid] + d[nxt].first , t.lstid , d[nxt].second}) ;
    	}
    	ind = t.curid ? v[t.curid] : 1;
    	if(rt[ind]){
    		int nxt = binary(1, m, 0, rt[ind]) ;
    		if(nxt != -1)	q.push({t.val + d[nxt].first , t.curid , d[nxt].second}) ;
    	}
	}
	cout << ans << '\n' ;
}


int main(){
	ios::sync_with_stdio(0) ,cin.tie(0) ,cout.tie(0) ;
	init() ;
	dij() ;
	solve() ;
	return 0 ;
}

0x20 无向图最小生成树

0x21 相关定义

核心思想：向生成树中加入一条边考察环的性质。

0x22 最小生成树问题

0x221 kruskal

时间复杂度：$\Theta(m\log m)$

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std ;
#define ll long long
const int MAXN = 5e3+10 ;
const int MAXM = 2e5+10 ;

ll n ,m ;
struct Edge{
	int to ,from ;
	ll w ;
}edge[MAXM] ;
int edge_cnt ;

inline bool cmp(Edge a , Edge b){
	return a.w < b.w ;
}

ll ans = 0 ;
int fa[MAXN] ;

inline int findd(int x){
	return x == fa[x] ? x : fa[x] = findd(fa[x]) ;
}

int main(){
	cin >> n >> m ;
	for(int i = 1;i <= m;++i){
		int u ,v ;ll w ;cin >> u >> v >> w ;
		edge[++edge_cnt] = (Edge){v , u , w} ;
	}
	sort(edge+1 , edge+1+m , cmp) ;
	for(int i = 1;i <= n;++i)	fa[i] = i ;
	for(int i = 1;i <= m;++i){
		int u = edge[i].from ,v = edge[i].to ;
		if(findd(u) == findd(v))	continue ;
		fa[findd(u)] = findd(v) ;
		ans += edge[i].w ;
	}
	int check = 0 ;
	for(int i = 1;i <= n;++i)	if(fa[i] == i)	check++ ;
	if(check > 1){
		cout << "orz" ;
		return 0 ;
	}
	cout << ans ;
	return 0 ;
}

0x222 Boruvka算法

这篇blog加上OI-WIKI上的动图
看起来很简单的样子。
时间复杂度$\Theta(T\log n)$其中T表示求minn[]的时间复杂度（可以使用线段树、主席树、权值等）

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std ;
#define ll long long
const int MAXN = 5e3+10 ;
const int MAXM = 2e5+10 ;

int n ,m ;
struct Edge{
	int to ,next ;ll w ;
}edge[MAXM<<1] ;
int head[MAXN] ,edge_cnt ;

inline void edge_add(int from , int to , ll w){
	edge[++edge_cnt].to = to ;
	edge[edge_cnt].next = head[from] ;
	edge[edge_cnt].w = w ;
	head[from] = edge_cnt ;
}

int fa[MAXN] ,minn[2][MAXN] ;

inline int findd(int x){
	return fa[x] == x ? x : fa[x] = findd(fa[x]) ;
}

int main(){
	cin >> n >> m ;
	for(int i = 1;i <= n;++i)	fa[i] = i ;
	for(int i = 1;i <= m;++i){
		int u ,v ,w ;cin >> u >> v >> w ;
		edge_add(u , v , w) ;edge_add(v , u , w) ;
	}
	ll ans = 0 ;
	while(1){
		memset(minn[0] , 0x7f , sizeof minn[0]) ;
		bool flag = 0 ;
		for(int u = 1;u <= n;++u){
			for(int i = head[u];i;i = edge[i].next){
				int v = edge[i].to ;ll w = edge[i].w ;
				if(findd(u) == findd(v))	continue ;
				if(minn[0][findd(u)] > w){
					minn[0][findd(u)] = w ;
					minn[1][findd(u)] = findd(v) ;
				}
			}
		}
		for(int i = 1;i <= n;++i)
			if(minn[0][i] != minn[0][0] && findd(i) != findd(minn[1][i])){
				flag = 1 ;
				ans += minn[0][i] ;
				fa[findd(i)] = findd(minn[1][i]) ;
			}
		if(!flag)	break ;
	}
	int cnt = 0 ;
	for(int i = 1;i <= n;++i)	if(fa[i] == i)	cnt++ ;
	if(cnt > 1){
		cout << "orz" ;
		return 0 ;
	}
	cout << ans ;
	return 0 ;
}

0x23 拟阵和生成树

拟阵简介+详细介绍推荐blog?

0x231 拟阵的定义和性质

拟阵的定义没啥好说的。
关于图拟阵：

定理1中“拟阵大小相同”应该是对于同一个图来说的。
我猜$z\in A\B$是元素$z$属于A集合且不属于B集合的意思。
基交换定理类似于带删除线性基中的操作（有线性基的底子可能更好理解）
图拟阵和生成树的关系体现在非线性关系上。这使得基交换定理在生成树上依旧成立。（感性理解）
$\land$ and ;$\lor$ or
秩函数的两个性质很好理解。

0x232 拟阵上的最优化问题

将生成树的kruskal算法推广到函数领域。

0x233 最小生成树的性质

主要研究最小权基的形态问题。
part1：所有权值不大于$w$的边具有什么样的共同特征？所有权值等于$w$的边呢？
首先，特殊情况很好理解：最小生成树肯定是唯一的，因此基也一定唯一。
然后思考普遍情况。突然发现这个证明很像考场上推出来的结论！
最后的两个推论很帅。感性理解，小于等于$w$的个数就是秩函数的大小。
最后的这个重要事实感觉很抽象。没见过这类的题捏。
好像就是将生成树的最大边划归为额定边，剩余缩点（内部不固定）。

0x24 拓展问题

注意LCT维护生成树手段（又没见过捏）。

0x241 次小生成树

次小生成树：通过基交换定理从差许多边调整至只差一条边：
由于既定的假设是一条边如果能被其他边替换，那么这条边才不在最小生成树上。所以，只有一种情况才不能被替换：同时有多条边存在被删除的边作为因子。这时只要再在这多条边中任选一条就重新有了这种因子就可以替换。
严格次小生成树：同样只差一条边
很符合直觉。相较非严格只是要多删几次边。
适用于所有拟阵。

0x242 k小生成树

你说得对，但是魏老师咕了。

0x243 最小生成树计数

你说得对，但是他啥都没说。
时间复杂度$\Theta(n^3)$

0x244 最小度限制生成树

感觉这几个都属于科技啊，%%%
感觉证明略复杂，但是代码很简单。
最复杂的部分在收集权值变化量部分。

注意这部分操作是为了保证在deg大于k而小于deg+delta.size()的时候计算用。

0x25 例题

0x251 P1967 [NOIP2013 提高组] 货车运输

水题，最大生成树加LCA倍增。

0x252 P4180 [BJWC2010] 严格次小生成树

仔细分讨，有点像k短路，但是不完全，需要维护一个max。

0x253 P4208 [JSOI2008] 最小生成树计数

模板题。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std ;

const int mod = 31011 ;
const int MAXN = 100+10 ;
const int MAXM = 1e3+10 ;

inline void add(int &x , int y){
	x = ((x + y) % mod + mod) % mod ;
}

int n ,m ;
int fa[MAXN] ,lab[MAXN] ,a[MAXN][MAXN] ;

inline int findd(int x){
	return x == fa[x] ? x : fa[x] = findd(fa[x]) ;
}

struct Edge{
	int from ,to ,w ;
}edge[MAXM] ,f[MAXN] ;

inline bool cmp(Edge x , Edge y){
	return x.w < y.w ;
}

inline void init(){
	for(int i = 1;i <= n;++i)	fa[i] = i ;
}

int main(){
	ios::sync_with_stdio(0) ;cin.tie(0) ;cout.tie(0) ;
	cin >> n >> m ; init() ;
	for(int i = 1;i <= m;++i)	cin >> edge[i].from >> edge[i].to >> edge[i].w ;
	sort(edge+1 , edge+1+m , cmp) ;
	int cnt = 0 ;
	for(int i = 1;i <= m;++i){
		int u = findd(edge[i].from) ,v = findd(edge[i].to) ;
		if(i == m && cnt < n-1){//缩点边数甚至构不成树 
			cout << 0 ;
			return 0 ;
		}
		if(u == v)	continue ;
		fa[v] = u ;
		f[++cnt] = edge[i] ;
	}
	int ans = 1 ;	
	for(int i = 1;i <= m;++i){//枚举边 
		int r = i ,tot = 0 ;
		while(r < m && edge[r+1].w == edge[i].w)	++r ;//不等于w的边都要缩起来 
		for(int j = 1;j <= n;++j)	fa[j] = j ;
		bool flag = 0 ;
		for(int j = 1;j < n;++j){
			if(f[j].w == edge[i].w)	flag = 1 ;
			else	fa[findd(f[j].to)] = findd(f[j].from) ;
		}
		if(flag){//不是缩成了只有一条边 
			memset(lab , 0 , MAXN<<2) ;
			for(int j = 1;j <= n;++j)	if(fa[j] == j)	lab[j] = ++tot ;//第几个连通块 
			memset(a , 0 , sizeof a) ;
			for(int j = i;j <= r;++j){
				int u = lab[findd(edge[j].from)] ,v = lab[findd(edge[j].to)] ;
				a[u][u]++ ;a[v][v]++ ;//入度 
				add(a[u][v] , mod-1) ;//连通块之间连边，邻接矩阵（应该是-1但是取模） 
				add(a[v][u] , mod-1) ; 
			}
			int det = 1 ,swp = 0 ;//辗转相处法求行列式 
			for(int j = 1;j < tot;++j){
				int p = j ;
				for(int k =	j+1;k < tot;++k)	if(a[k][j])	p = k ;
				if(j < p)	swap(a[j] , a[p]) ,swp ^= 1 ;
				if(!a[j][j]){
					cout << 0 ;
					return 0 ;
				}
				for(int k = j+1;k < tot;++k){
					while(a[k][j]){
						int d = a[j][j] / a[k][j] ;
						for(int t = j;t < tot;++t)	add(a[j][t] , mod-1ll*d*a[k][t]%mod) ;
						swap(a[j] , a[k]) ,swp ^= 1 ; 
					}
				}
			}
			for(int j = 1;j < tot;++j) det = 1ll * det * a[j][j] % mod ;//行列式求值 
    		if(swp)	det = mod - det ;//奇数次变换为负数 
    		ans = 1ll * ans * det % mod ;
		}
		i = r ;
	}
	cout << ans ;
	return 0 ;
}

0x254 P5633 最小度限制生成树

模板题。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std ;

const int MAXN = 5e5+10 ;

int n ,m ,s ,k ;
int val[MAXN] ,fa[MAXN] ;
int ans = 0 ,edge_cnt = 0 ;
struct Edge{
	int from ,to ,w ;
	bool operator < (const Edge &z) const{
		return w < z.w ;
	}
}edge[MAXN] ;

inline void init(){
	memset(val , 0x7f , sizeof val) ;
	for(int i = 1;i <= n;++i)	fa[i] = i ;
}

inline int findd(int x){
	return fa[x] == x ? x : fa[x] = findd(fa[x]) ;
}

int main(){
	ios::sync_with_stdio(0) ;cin.tie(0) ;cout.tie(0) ;
	cin >> n >> m >> s >> k ;
	init() ;
	for(int i = 1;i <= m;++i){
		int u ,v ,w ;cin >> u >> v >> w ;
		if(u == s)	val[v] = min(val[v] , w) ;//u或v是目标节点：更新点权（1和它之间的边权） 
		else if(v == s)	val[u] = min(val[u] , w) ;
		else edge[++edge_cnt] = {u,v,w} ;//与源节点相连的边不需要建边，edge_cnt != m 
	}
	sort(edge+1 , edge+1+edge_cnt) ;//贪心排序 
	vector<int>	delta ;
	for(int i = 1;i <= edge_cnt;++i){//从最小的开始枚举 
		int u = findd(edge[i].from) ,v = findd(edge[i].to) ;
		if(u == v)	continue ;//已经位于同一个连通块 
		if(val[u] > val[v])	swap(u , v) ;//假设出边点权最大 
		fa[v] = u ;//合并成同一个连通块 
		ans += edge[i].w ;//这条边一定要取 （是v使得u更新） 
		if(val[v] < 1e9)	delta.push_back(val[v] - edge[i].w) ;//收集权值变化量 
	}
	int deg = 0 ;//记录最小需要的度数 
	for(int i = 1;i <= n;++i){
		if(fa[i] != i || i == s)	continue ;//连通块的最大节点或源节点都不能计算点权 
		if(val[i] > 1e9){//前面已经特判了不是和源节点直接相连的节点，所以如果还是有无穷大就是不连通 
			cout << "Impossible\n" ;
			return 0 ;
		}
		deg++ ;//基础度多了1 
		ans += val[i] ;//这几条边权必须取 
	}
	return 0 ;
	if(deg > k || deg + delta.size() < k){//最小度数都大于k 或 将所有和源节点相连的边都去掉 都达不到k 
		cout << "Impossible\n" ;
		return 0 ;
	}
	sort(delta.begin() , delta.end()) ;//排序，求最小 
	for(int i = 0;i < k-deg;++i)	ans += delta[i] ;
	cout << ans ;
	return 0 ;
}

0x255 CF888G Xor-MST

感觉这道题更好的解法还是利用Boruvka的思想解决这类特殊的最小生成树问题。
思考Boruvka算法的关键流程：

当前每个集合伸出去一条最短的边，然后把联通块缩成一个新的集合，因为每次缩集合个数减半，所以复杂度对。

这道题就可以将集合之间的合并变成对trie树的合并，利用好两个性质：

异或只需要寻找二进制的不同项
生成树每个点都要到，并且边权和点权还有关联
其中“连续区间”的性质感觉好像可以不利用，直接用vector也可。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm> 
using namespace std ;
#define ll long long
const int MAXN = 2e5+10 ;
const int INF = 0x7f7f7f7f ;

int n ,cnt ;
int ch[MAXN*40][2] ,a[MAXN] ;
int rt ,l[MAXN*40] ,r[MAXN*40] ;//01trie空间大小为30*2 

inline void insert(int &node , int x , int dep){
	if(!node)	node = ++cnt ;//动态开点 
	l[node] = min(l[node] , x) ;r[node] = max(r[node] , x) ;//维护每个节点的点边号区间，相当于插入操作 
	if(dep < 0)	return ;//必须放在最后：需要终止符 
	int bit = a[x] >> dep & 1 ;//从最高位开始依次插入01trie 
	insert(ch[node][bit] , x , dep-1) ;
}

inline int query(int node , int val , int dep){//寻找接下来需要异或的最小数 
	if(dep < 0)	return 0 ;
	int bit = val >> dep & 1 ;
	if(ch[node][bit])	return query(ch[node][bit] , val , dep-1) ;
	//如果这意味有数值，说明存在这个数，不需要有另外一个数去异或得到目标val 
	else	return query(ch[node][bit^1] , val , dep-1) + (1 << dep) ;
	//否则就需要加上需要异或的数 
}

inline ll dfs(int node , int dep){
	if(dep < 0)	return 0 ;
	if(r[ch[node][0]] && r[ch[node][1]]){//左右区间都还有数值 
		int minn = INF ;
		for(int i = l[ch[node][0]];i <= r[ch[node][0]];++i)	minn = min(minn , query(ch[node][1] , a[i] , dep-1)) ;
	//只需要枚举任意一个分枝，因为最小异或代价都是相同的 
		return dfs(ch[node][0] , dep-1) + dfs(ch[node][1] , dep-1) + minn + (1 << dep) ;
	//后面的部分表示选取两个点所需要付出的代价，前面两个dfs表示递推操作
	//之前的两个点01串完全相同，因此异或后为0；经过这个点后不同，且异或后一定为1，所以(1<<dep) 
	}else if(r[ch[node][0]]){
		return dfs(ch[node][0] , dep-1) ;
	}else if(r[ch[node][1]]){
		return dfs(ch[node][1] , dep-1) ;
	}
}

int main(){
	ios::sync_with_stdio(0) ;cin.tie(0) ;cout.tie(0) ;
	cin >> n ;
	for(int i = 1;i <= n;++i)	cin >> a[i] ;
	sort(a+1 , a+1+n) ;memset(l , 0x7f , sizeof l) ;//按照点权大小排序，使得在插入01trie时候区间连续 
	for(int i = 1;i <= n;++i)	insert(rt , i , 30) ;//将每个点都插入01trie 
	cout << dfs(rt , 30) ;//相当于从最大的区间直接查询最小生成树 
	return 0 ;
}

0x256 CF1305G Kuroni and Antihype

Boruvka算法。考虑首先计算出来贡献，再累加。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std ;
#define ll long long
#define pii pair<int,int>
const int MAXN = 2e5+10 ;
const int MAXT = 1<<18 ;

int n ;
ll ans ;
int a[MAXN] ,fa[MAXN] ,siz[MAXN] ;
pii large[MAXN] ;
pii best[MAXT+10][2] ;

inline int findd(int x){
	return x == fa[x] ? x : fa[x] = findd(fa[x]) ;
}

inline bool merge(int u , int v){
	int x = findd(u) ,y = findd(v) ;
	if(x == y)	return 0 ;
	if(siz[x] > siz[y])	swap(x , y) ;
	fa[x] = y ;
	siz[y] += siz[x] ;
	return 1 ;
}

inline void init(){
	for(int i = 1;i <= n+1;++i)	fa[i] = i ,siz[i] = 1 ;
}

inline void trans(pii a[2] , pii b[2]){//更新最大值、次大值关系 
	for(int i = 0;i < 2;++i){
        pii t = b[i] ;
        if(t.first > a[0].first || (t.first == a[0].first && t.second != a[0].second)){
            if(a[0].second != t.second)
                a[1] = a[0] ;
            a[0] = t ;
        }
        else if(t.first > a[1].first && t.second != a[0].second)
            a[1] = t ;
    }
}

int main(){
	ios::sync_with_stdio(0) ;cin.tie(0) ;cout.tie(0) ;
	cin >> n ;init() ;//将边权(i,j)定义为a_i + a_j，转变成求最大生成树 
	for(int i = 1;i <= n;++i)	cin >> a[i] ,ans -= a[i] ;//边权值要减去每个点的权值 
	int tot = n + 1 ;//总共有n+1个连通块 
	while(tot > 1){//最后合并成1个连通块 
		for(int i = 0;i < MAXT;++i)	best[i][0] = best[i][1] = make_pair(-1,-1) ;
		for(int i = 1;i <= n+1;++i){
			int id = findd(i) ;//0表示最大值，1表示次大值 
			if(best[a[i]][0].second == -1)	best[a[i]][0] = make_pair(a[i] , id) ;//初始化最大值 
			else if(best[a[i]][1].second == -1 && best[a[i]][0].second != id)	best[a[i]][1] = make_pair(a[i] , id) ;//初始化次大值 
		}
		for(int i = 0;i < 18;++i)//枚举位数 
			for(int s = 0;s < MAXT;++s)//枚举每种情况 
				if(s >> i & 1){//这一位上有1 
					int t = s ^ 1 << i ;//位运算优先级大于异或 
					trans(best[s] , best[t]) ;
				}
		for(int i = 1;i <= n;++i)	large[i] = make_pair(-1,-1) ;
		for (int i = 1;i <= n+1;++i){
            int s = (MAXT - 1) ^ a[i] ,id = findd(i) ;
            if (best[s][0].first == -1)//不存在 
                continue ;
            if ((best[s][0].first ^ a[i]) > large[id].first && best[s][0].second != id)//更新答案 
                large[id] = best[s][0] ,large[id].first ^= a[i] ;
            if ((best[s][1].first ^ a[i]) > large[id].first && best[s][1].second != id)
                large[id] = best[s][1] ,large[id].first ^= a[i] ;
        }
        for (int i = 1;i <= n+1;++i)	if(findd(i) == i && large[i].first != -1 && merge(large[i].second , i))	--tot ,ans += large[i].first ;
        //统计答案 
	}
	cout << ans ;
	return 0 ;
}

0x30 无向图连通性：双连通分量

0x31 相关定义

注意边双和点双缩点后都是一棵树。

0x32 双连通的基本性质

研究双连通的性质时，最重要的是把定义中的基本元素 —— 割点和割边的性质理清楚。然后从整体入手，考察对应分量在原图上的分布形态，再深入单个分量，考察分量内两点之间的性质。以求对该连通性以及连通分量有直观的印象，思考时有清晰的图像作为辅助，做题思路更流畅。——Alex_Wei

0x321 边双连通

基础介绍。

0x322 点双连通

点双之间可能会有一个交点。这个交点一定是割点。
由“1”推出结论：一个点是割点当且仅当它属于超过一个点双。
块状树由割点+缩点组成
对于$n\leqslant 3$的点双内任意一点$u$,存在经过$u$的简单环。
在$n=1 or 2$的情况下：1时显然不成立（连边都没有）；2时只有一条边（此时是点双不是边双）

0x323 门杰定理及其推论

门杰定理就是网络流中“最大流=最小割”在边双和点双之间的应用。
点-边转化技巧使得门杰定理得以在任何双连通图中得以运用。
四种定义，很好理解。

0x324 双连通总结

如果一张点数大于$2$的图没有割点，那么它一定没有割边。假设存在割边，那么删去割边后大小大于$1$的连通块对应的割边端点一定是割点。（很明显）
任何边双满足的性质，点数大于$2$的点双一定满足。
一般 “不经过重复边” 的问题借助边双解决，而 “不经过重复点” 的问题借助点双解决
每个点恰属于一个边双，每条边可能恰属于一个边双（非割边），也可能不属于任何边双（割边）；每条边恰属于一个点双，每个点可能属于一个点双（非割点），也可能属于多个点双（割点）。【说明：点双>>边双】

0x325 点双连通的更多性质

三条性质都是点双上任意两点形成闭环回路的推论。

0x33 Tarjan 求割点

0x331 非根的节点判定

是特殊情况：$T'(x)$非空。
求割点的原理十分深刻！很好理解！

0x332 根的割点判定与代码

就是将度数不为1时候特判为割点。

#include<iostream>
#include<cstdio>
using namespace std ;

const int MAXN = 2e4+10 ;
const int MAXM = 1e5+10 ;

struct Edge{
	int to ,next ;
}edge[MAXM<<1] ;
int head[MAXN] ,edge_cnt ;

inline void edge_add(int from , int to){
	edge[++edge_cnt].to = to ;
	edge[edge_cnt].next = head[from] ;
	head[from] = edge_cnt ;
}

int n ,m ;
int tim ,rt ,cnt ;
int low[MAXN] ,dfn[MAXN] ;
bool buc[MAXN] ;

inline void tarjan(int node){
	low[node] = dfn[node] = ++tim ;
	int son = 0 ;
	for(int i = head[node];i;i = edge[i].next){
		int v = edge[i].to ;
		if(!dfn[v]){
			son++ ;
			tarjan(v) ;
			low[node] = min(low[node] , low[v]) ;
			if(low[v] >= dfn[node] && node != rt)	cnt += !buc[node] ,buc[node] = 1 ;
		}else
			low[node] = min(low[node] , dfn[v]) ;
	}
	if(son >= 2 && node == rt)	cnt += !buc[node] ,buc[node] = 1 ;
}

int main(){
	ios::sync_with_stdio(0) ;cin.tie(0) ;cout.tie(0) ;
	cin >> n >> m ;
	for(int i = 1;i <= m;++i){
		int u ,v ;cin >> u >> v ;
		edge_add(u , v) ,edge_add(v , u) ;
	}
	for(int i = 1;i <= n;++i)	if(!dfn[i])	rt = i ,tarjan(i) ;
	cout << cnt << '\n' ;
	for(int i = 1;i <= n;++i)	if(buc[i])	cout << i << ' ' ;
	return 0 ;
}

0x34 割边的求法

时间复杂度均为$\Theta(n+m)$。

0x341 Tarjan

和割点很像，只不过链式前向星判断树边时需要对边的边号进行异或操作，所以不如直接用vector将边号直接加入。

0x342 树上差分法

好像没太学会（？

0x35 边双连通分量缩点

首先，魏老师放错代码了。。。
~~害的我想了半天为什么要用割边求点双~~

#include<iostream>
#include<cstdio>
#include<vector>
#include<cstring>
using namespace std ;

const int MAXN = 5e5+10 ;
const int MAXM = 2e6+10 ;

struct Edge{
	int to ,next ;
}edge[MAXM<<1] ;
int edge_cnt = 1 ,head[MAXN] ;

inline void edge_add(int from , int to){
	edge[++edge_cnt].next = head[from] ;
	edge[edge_cnt].to = to ;
	head[from] = edge_cnt ;
}

int n ,m ;
vector<vector<int> > ans ;
int dfn[MAXN] ,low[MAXN] ,tim ;
int stack[MAXN] ,top ;

inline void form(int u , int v){
	vector<int> dcc ;dcc.push_back(u) ;
	for(int i = 0;i != v;)	dcc.push_back(i = stack[top--]) ;
	ans.push_back(dcc) ;
}

inline void tarjan(int node){
	dfn[node] = low[node] = ++tim ;
	stack[++top] = node ;
	for(int i = head[node];i;i = edge[i].next){
		int v = edge[i].to ;
    	if(!dfn[v]){
    		tarjan(v) ,low[node] = min(low[node] , low[v]) ;
    		if(low[v] >= dfn[node]) form(node , v) ;
    	}
    	else low[node] = min(low[node], dfn[v]);
	}
}

int main(){
	ios::sync_with_stdio(0) ;cin.tie(0) ;cout.tie(0) ;
	cin >> n >> m ;
	for(int i = 1;i <= m;++i){
		int u ,v ;cin >> u >> v ;
		if(u == v)  continue ;
		edge_add(u , v) ;edge_add(v , u) ;
	}
	for(int i = 1;i <= n;++i){
		if(!head[i]){
			vector<int>	dcc ;dcc.push_back(i) ;ans.push_back(dcc) ;
		}
		else if(!dfn[i])	tarjan(i) ;
	}
	cout << ans.size() << '\n' ;
	for(int i = 0;i < ans.size();++i){
		cout << ans[i].size() << ' ' ;
		for(int j = 0;j < ans[i].size();++j)	cout << ans[i][j] << ' ' ;
		cout << '\n' ;
	}
	return 0 ;
}

顺便把割边的代码也放一下：
P8436 【模板】边双连通分量
注意 vis数组不需要清空！

#include<iostream>
#include<cstdio>
#include<vector>
#include<cstring>
using namespace std ;

const int MAXN = 5e5+10 ;
const int MAXM = 2e6+10 ;

struct Edge{
	int to ,next ;
}edge[MAXM<<1] ;
int edge_cnt = 1 ,head[MAXN] ;

inline void edge_add(int from , int to){
	edge[++edge_cnt].next = head[from] ;
	edge[edge_cnt].to = to ;
	head[from] = edge_cnt ;
}

int n ,m ;
vector<vector<int> > ans ;
int dfn[MAXN] ,low[MAXN] ,tim ;
int stack[MAXN] ,top ;

inline void form(int x){
	vector<int> ecc ;
	for(int i = 0;i != x;)	ecc.push_back(i = stack[top--]) ;
	ans.push_back(ecc) ;
}

bool vis[MAXM] ;

inline void tarjan(int node , int edgeid){
	dfn[node] = low[node] = ++tim ;
	stack[++top] = node ;
	for(int i = head[node];i;i = edge[i].next){
		if(vis[i])	continue ;
		vis[i] = vis[i^1] = 1 ;
		int v = edge[i].to ;
		if(!dfn[v]){
			tarjan(v , i) ;
			low[node] = min(low[node] , low[v]) ;
			if(low[v] > dfn[node])	form(v) ;
		}else	low[node] = min(low[node] , dfn[v]) ; 
	}
}

int main(){
	ios::sync_with_stdio(0) ;cin.tie(0) ;cout.tie(0) ;
	cin >> n >> m ;
	for(int i = 1;i <= m;++i){
		int u ,v ;cin >> u >> v ;
		edge_add(u , v) ;edge_add(v , u) ;
	}
	for(int i = 1;i <= n;++i)	if(!dfn[i])	tarjan(i , 0) ,form(i) ;
	cout << ans.size() << '\n' ;
	for(int i = 0;i < ans.size();++i){
		cout << ans[i].size() << ' ' ;
		for(int j = 0;j < ans[i].size();++j)	cout << ans[i][j] << ' ' ;
		cout << '\n' ;
	}
	return 0 ;
}

0x36 例题

0x361 P3469 [POI2008] BLO-Blockade

小心$u$本身没有删去。

0x362 P2860 [USACO06JAN] Redundant Paths G

公式，很容易找到。

0x363 CF51F Caterpillar

缩点模板题,再套上一个树的直径。性质题。

0x40 有向图可达：强连通分量

0x41 相关定义

没啥说的。

0x42 有向图DFS树

弱连通图：如果将所有有向边替换成无向边之后连通，那么这幅图就是弱连通图。
DFS树可能是森林，因此要多次遍历。

0x43 Tarjan求SCC

重要结论：对于两个SCC S1,S2，若 S1 可达 S2，则S1比S2后弹出栈。按弹出顺序写下所有 SCC，得到缩点 DAG 的反拓扑序。因此，按编号从大到小遍历 SCC，就是按拓扑序遍历缩点 DAG，省去了拓扑排序。
P3387 【模板】缩点

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std ;

const int MAXN = 1e4+10 ;

vector<int>	e[MAXN] ,g[MAXN] ;
int n ,m ;
int cnt ,col[MAXN] ;
int a[MAXN] ,val[MAXN] ,f[MAXN] ;
int stack[MAXN] ,top ,scc[MAXN] ,tim ,dfn[MAXN] ,low[MAXN] ;
bool vis[MAXN] ;

inline void tarjan(int node){
	dfn[node] = low[node] = ++tim ;
	vis[node] = 1 ;
	stack[++top] = node ;
	for(int i = 0;i < e[node].size();++i){
		int v = e[node][i] ;
		if(!dfn[v]){
			tarjan(v) ;
			low[node] = min(low[v] , low[node]) ;
		}else if(vis[v])	low[node] = min(low[node] , dfn[v]) ;
	}
	if(dfn[node] == low[node]){
		col[node] = ++cnt ;
		while(stack[top] != node)	col[stack[top]] = cnt ,vis[stack[top--]] = 0 ;
		vis[node] = 0 ,top-- ;
	}
}

int main(){
	ios::sync_with_stdio(0) ;cin.tie(0) ;cout.tie(0) ;
	cin >> n >> m ;
	for(int i = 1;i <= n;++i)	cin >> a[i] ;
	for(int i = 1;i <= m;++i){
		int u ,v ;
		cin >> u >> v ;
		e[u].push_back(v) ;
	}
	for(int i = 1;i <= n;++i)	if(!dfn[i])	tarjan(i) ;
	for(int i = 1;i <= n;++i){
		val[col[i]] += a[i] ;
		for(int j = 0;j < e[i].size();++j){
			int v = e[i][j] ;
			if(col[v] != col[i])	g[col[i]].push_back(col[v]) ;
		}
	}
	int ans = 0 ;
	for(int i = cnt;i;--i){
		f[i] += val[i] ;
		ans = max(ans , f[i]) ;
		for(int j = 0;j < g[i].size();++j)	f[g[i][j]] = max(f[g[i][j]] , f[i]) ;
	}
	cout << ans ;
	return 0 ;
}

0x44 Kosaraju算法

第二次DFS：由于离开性质，其他边不可达。更详细的解释
目前缺少模板题。现只有两个代码共参考：
kosaraju+bitset
kosaraju+bitset+莫队

0x45 例题

0x451 P3436 [POI2006] PRO-Professor Szu

很水的SCC反图拓扑序板题。一开始在36500上纠结很久（担心有的值（非无穷解）的答案以也会大于这个数）后来发现没有关系，因为就是累加，只需要覆盖就可以。

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std ;

const int INF = 36501 ;
const int MAXN = 1e6+10 ;

int n ,m ;
struct Edge{
	int next ,to ;
}edge[MAXN] ,g[MAXN] ;
int head[MAXN] ,edge_cnt ;
int hg[MAXN] ,g_cnt ;

inline void edge_add(int from , int to){
	edge[++edge_cnt].next = head[from] ;
	edge[edge_cnt].to = to ;
	head[from] = edge_cnt ;
}

inline void g_add(int from , int to){
	g[++g_cnt].next = hg[from] ;
	g[g_cnt].to = to ;
	hg[from] = g_cnt ;
}

int low[MAXN] ,dfn[MAXN] ,tim ,col[MAXN] ,cnt ;
int stack[MAXN] ,top ;
bool vis[MAXN] ;

inline void tarjan(int node){
	dfn[node] = low[node] = ++tim ;
	stack[++top] = node ;vis[node] = 1 ;
	for(int i = head[node];i;i = edge[i].next){
		int v = edge[i].to ;
		if(!dfn[v]){
			tarjan(v) ;
			low[node] = min(low[node] , low[v]) ;
		}else if(vis[v])	low[node] = min(low[node] , dfn[v]) ;
	}
	if(low[node] == dfn[node]){
		col[node] = ++cnt ;
		while(stack[top] != node)	col[stack[top]] = cnt ,vis[stack[top--]] = 0 ;
		vis[stack[top--]] = 0 ;
	}
}

bool ban[MAXN] ;
int f[MAXN] ;

int main(){
	ios::sync_with_stdio(0) ;cin.tie(0) ;cout.tie(0) ;
	cin >> n >> m ;++n ;
	for(int i = 1;i <= m;++i){
		int u ,v ;cin >> u >> v ;
		edge_add(u , v) ;
	}
	for(int i = 1;i <= n;++i)	if(!dfn[i])	tarjan(i) ;
	for(int i = 1;i <= n;++i){
		for(int j = head[i];j;j = edge[j].next){
			int v = edge[j].to ;
			if(col[i] == col[v])	ban[col[i]] = 1 ;
			else g_add(col[v] , col[i]) ;//建反边：离终点越远方案数越大 
		}
	}
	f[col[n]] = 1 ;
	for(int i = 1;i <= cnt;++i){
		if(f[i] && ban[i])	f[i] = INF ;
//由于建的是反图，如果有值为正（说明可以直接到达n+1）并且还在SCC中，说明可以走无穷次边。 
		for(int j = hg[i];j;j = g[j].next){
			int v = g[j].to ;
			f[v] = min(f[v]+f[i] , INF) ;
		}
	}
	int maxx = 0 ;
	vector<int> ans ;
	for(int i = 1;i < n;++i){
		if(f[col[i]] > maxx)	maxx = f[col[i]] ,ans.clear() ;
		if(maxx == f[col[i]])	ans.push_back(i) ;
	}
	if(maxx == INF)	cout << "zawsze\n" ;
	else cout << maxx << '\n' ;
	cout << ans.size() << '\n' ;
	for(int i = 0;i < ans.size();++i)	cout << ans[i] << ' ' ;
	return 0 ;
}

0x452 P7737 [NOI2021] 庆典

叶向树形图，是说这张图的基图是一棵树，所有的边全部指向儿子。
性质题。首先观察到一个点被选取作为节点的必要条件。
使用类似虚树的方法统计答案。

0x453 AT_arc092_d [ARC092F] Two Faced Edges

Bitset优化图的遍历：每次找到 u 的所有出边中第一个没有被访问的点。具体地，设 vis表示每个结点是否访问过，e[u] 表示 u 的所有出边，则 (~vis & e[u])._Find_first()即为所求。
序列去掉一个位置的信息可由前缀和后缀合并得到。
为什么需要两边dfs？
ans[]表示当删去前面的一条边的时候是否能够依旧到达。当两次DFS之后，ans[]表示的就是如果这条边被删除后，两边的边能否到达。这也就是“由前缀和后缀合并得到”。

注释：

#include <bits/stdc++.h>
using namespace std;

constexpr int N = 1e3 + 5;
constexpr int M = 2e5 + 5;

int n, m;
int cnt, hd[N], nxt[M], to[M], ans[M];
void add(int u, int v) {nxt[++cnt] = hd[u], hd[u] = cnt, to[cnt] = v;}

int dn, dfn[N], low[N], cn, col[N], top, stc[N];
bitset<N> e[N], vis;
void tarjan(int id) {
  low[id] = dfn[id] = ++dn, stc[++top] = id, vis[id] = 1;
  for(int i = hd[id]; i; i = nxt[i]) {
    int it = to[i];
    if(!dfn[it]) tarjan(it), low[id] = min(low[id], low[it]);
    else if(vis[it]) low[id] = min(low[id], dfn[it]);
  }
  if(dfn[id] == low[id]) {
    col[id] = ++cn;
    while(stc[top] != id) vis[stc[top]] = 0, col[stc[top--]] = cn;
    vis[id] = 0, top--;
  }
}

int mark;
void dfs(int id) {
  vis[id] = 1;
  if(id == mark) return;
  while(1) {
    bitset<N> out = ~vis & e[id];
    int p = out._Find_first();
    if(p == N) break;
    dfs(p);
  }
}

int main() {
  cin >> n >> m;
  for(int i = 1; i <= m; i++) {
    int u, v;
    scanf("%d%d", &u, &v);
    add(u, v), e[u][v] = 1;
  }
  for(int i = 1; i <= n; i++) if(!dfn[i]) tarjan(i);
  for(int i = 1; i <= n; i++) {
    mark = i;
    static int out[N], len;
    len = 0, vis.reset();
    for(int j = hd[i]; j; j = nxt[j]) {//枚举v表示删除的边
      if(vis[to[j]]) ans[j] = 1;//删去此边依旧可到达
      else dfs(to[j]);
      out[++len] = j; //便于反向搜索
    }
    vis.reset();
    for(int p = len; p; p--) {
      int j = out[p];
      if(vis[to[j]]) ans[j] = 1;
      else dfs(to[j]);
    }
  }
  for(int i = 1; i <= n; i++)
    for(int j = hd[i]; j; j = nxt[j])
      ans[j] ^= col[i] != col[to[j]];//这条边是SCC之间的边：判断反向是否能到达
  for(int i = 1; i <= m; i++) puts(ans[i] ? "same" : "diff");
  return 0;
}

0x50 欧拉回路

0x51 相关定义

没啥说的。

0x52 欧拉路的判定

0x521 有向图

欧拉图：弱连通+每个点入度=出度
半欧拉图：弱连通+存在两个点入度=出度-1或+1其余点出入度相等

0x522 无向图

欧拉图：连通+每个点度数为偶数
半欧拉图：连通+有两个点入度为奇数，其余点度数为偶数

0x523 混合图

注意，这里的奇数度数指入度+出度

欧拉图：弱连通+网络流
（1）无解情况：
奇度数点；所有有向边入度或出度大于$\frac{d(i)}{2}$；跑完网络流后不符合（2）。
（2）有解情况：最大流为无向边总数，则有解，且当前流给出了一种定向方案。
跑完网络流后
半欧拉图：弱连通+有两个奇数点+枚举两个奇数点谁为起点跑网络流。

0x53 Hierholzer 算法

算法核心：不断往回路中中插入环。
步骤：遍历当前点u的所有出边u→v。若该边未走过，则向点vDFS。遍历完所有出边后，将u加入回路。最终得到一条反着的欧拉回路（图有向，且倒序加入环），将其翻转即可。
P7771 【模板】欧拉路径

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std ;

const int MAXN = 2e5+10 ;

int head[MAXN] ;//当前弧优化：记忆一下到哪条边了 
int n ,m ,lar ;
vector<int>	edge[MAXN] ;
int indeg[MAXN] ;
int top ,stack[MAXN] ;

inline void dfs(int node){
	for(int &i = head[node];i < edge[node].size();) dfs(edge[node][i++]) ;
	stack[++top] = node ;
}

inline int abs(int x){
	return x < 0 ? -x : x ;
}

int main(){
	ios::sync_with_stdio(0) ;cin.tie(0) ;cout.tie(0) ;
	cin >> n >> m ;
	for(int i = 1;i <= m;++i){
		int u ,v ;cin >> u >> v ;
		edge[u].push_back(v) ;
		indeg[v]++ ;
	}
	for(int i = 1;i <= n;++i){
		sort(edge[i].begin() , edge[i].end()) ;
		if(abs((int)(edge[i].size()) - indeg[i]) > 1){//出度和入度差大于1 
			printf("No") ;
			return 0 ;
		}
		if(edge[i].size() == indeg[i]+1){//出度等于入度+1 
			if(lar){//起点 
				cout << "No" ;
				return 0 ;
			}else lar = i ;
		}
	}
	dfs(lar ? lar : 1) ;
	if(top != m + 1) cout << "No" ; // 图不连通
	else{
    	reverse(stack+1 , stack+top+1) ;//反转数组 
    	for(int i = 1;i <= top;++i)	cout << stack[i] << " " ;
	}
	return 0 ;
}

0x54 例题

0x541 P2731 [USACO3.3] 骑马修栅栏 Riding the Fences

板子题。

0x542 P1127 词链

注意，对邻接链表排序要按照每条边对应字符串的字典序排序，而非指向结点的编号大小。

#include<iostream>
#include<cstdio>
#include<vector>
#include<string>
#include<cstring>
#include<algorithm> 
using namespace std ;
#define psi pair<string, int>
const int MAXN = 1000 + 5 ;

int n ,deg[26] ,head[26] ;
vector<psi> edge[26] ;
vector<string> ans ;

inline void dfs(int node) {
	for(int &i = head[node]; i < edge[node].size();){
		psi dat = edge[node][i++] ;
		dfs(dat.second) ;
		ans.push_back(dat.first) ;
	}
}

int main() {
	ios::sync_with_stdio(0) ;cin.tie(0) ;cout.tie(0) ; 
	cin >> n ;
	for(int i = 1;i <= n;++i){
		string str ;
		cin >> str ;
		edge[str[0] - 'a'].push_back({str , str[str.length()-1] - 'a'}) ;
		deg[str[str.length()-1] - 'a']++ ;
	}
	int s = -1;
	for(int i = 0;i < 26;++i){
		sort(edge[i].begin() , edge[i].end()) ;
		if(abs(deg[i] - int(edge[i].size())) > 1){
			cout << "***" ;
			return 0 ;
		}
		if(edge[i].size() == deg[i] + 1){
			if(s != -1){
				cout << "***" ;
				return 0 ;
			}
			else s = i;
		}
	}
	for(int i = 0;i < 26 && s == -1;++i) if(deg[i]) s = i ;
	dfs(s) ;
	reverse(ans.begin() , ans.end()) ;
	if(ans.size() != n){
		cout << "***" ;
		return 0 ;
	}
	for(int i = 0;i < ans.size();++i){
		if(i) cout << '.' ;
		cout << ans[i] ;
	}
	return 0 ;
}